Основные законы механики сплошной среды

Реальные материальные системы могут быть как дискретными, так и сплошными, представляющими непрерывное распределение вещества и физических свойств его состояния. Такие среды называют сплошными. Обладая общим свойством непрерывности, тела сильно отличаются по своим физическим свойствам: состоят из совокупности молекул и атомов различного сорта, с различными расстояниями между ними. Могут состоять из элементов с избытком или недостатком электронов.

Сплошность среды заключается в том, что даже в малом объеме содержится большое число молекул так, что расстояния между ними («пустоты») сравнимы с размерами этих молекул.

Обычно в механических объектах расстояния между молекулами очень малы так, что возникают очень большие силы сцепления. Особенно большими эти силы бывают на поверхностях раздела.

Главными характеристиками сплошной среды являются плотность, давление, температура и так далее.

Закон сохранения массы (уравнение неразрывности)

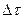- малый объем в окрестности т. М

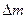- масса этого объема

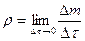- плотность

В технике иногда 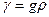(удельный вес или массовая плотность)

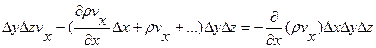
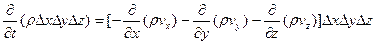
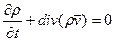
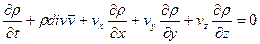
- уравнение неразрывности

Понятие модели, классификация моделей

Модель – это какое-либо описание системы некоторыми средствами. В естественных науках модели разрабатываются обычно на основе теоретических законов и принципов. Моделями могут быть масштабированные физические объекты (иконические модели), математические уравнения и взаимосвязи (абстрактные модели) или графические представления объектов (визуальные модели).

Разработка модели – процесс сложный, который во многих своих моментах близок к искусствам, но, он, однако, упрощается, если:

1. известны физические законы, описывающие функционирование системы

2. может быть разработано графическое представление системы

3. можно управлять входами, элементами и выходами системы.

Моделирование сложных крупномасштабных систем (например, крупный завод или отрасль производства) чаще всего представляет собой более трудную задачу, чем моделирование физических систем или процессов. Это объясняется следующими причинами:

1. недостаточность числа фундаментальных законов, описывающих систему

2. большинство взаимосвязей между элементами в системе не поддаются количественному описанию и формализации или поддаются с трудом

3. не описывается количественно поведение входных элементов

4. наличием случайных процессов

5. составной частью системы является процесс принятия решения человеком.

Прежде чем переходить к вопросам построения имитационных моделей остановимся на понятии «модель» более подробно; приведем классификацию моделей.

Модели (вообще) подразделяются на две основные группы: вещественные (иконические) и символические (абстрактные). Последние делятся на словесно-описательные и математические. Словесно-описательные модели позволяют достаточно полно описать процесс, ситуацию или объект, но их невозможно использовать для анализа формализованным путем. Поэтому словесно-описательные модели преобразуют, как правило, в математические модели для удобства дальнейшего оперирования с ними.

Математическая модель – это совокупность математических объектов (чисел, переменных, векторов, множеств и т.д.) и отношений между ними, которая адекватно отображает некоторые свойства моделируемого объекта. Например, большой и важный класс математических моделей составляют системы уравнений.

Формирование математических моделей (раньше и сейчас) называют моделированием объекта. Но в последнее время к понятию моделирование стали относиться еще и оперирование моделью с целью получения полезной информации об исследуемом объекте.

В зависимости от характера отображаемых свойств моделируемого объекта математические модели делятся на функциональные и структурные. Функциональные отображают процессы функционирования объекта; они чаще всего имеют форму систем уравнений; нередки случаи использования моделей отображающих только структурные (в частности, геометрические) свойства объекта. Структурные модели могут иметь форму матриц, графов, списков векторов выражать взаимное расположение элементов в пространстве, наличие непосредственных связей между элементами и т.д.

По способам получений функциональные математические модели делят на теоретические и формальные. Первые строятся на основе изучения физических закономерностей. Последние получают на основе проявления свойств моделируемого объекта во внешней среде, то есть при рассмотрении объекта как кибернетического «черного ящика».

Приведем теперь схему – классификацию моделей:

Дата добавления: 2015-05-26