Основы подобия и моделирования

1. Общие положения теории подобия.

В основе методов моделирования лежит учение о подобии, основы которого заложены еще И Ньютоном.

Чтобы получить корректные результаты необходимо обеспечить подобие модели и натуры, т. е.

а) подобие геометрических свойств систем;

б) пропорциональность физических констант, имеющих существенное значение в изучаемом процессе;

в) подобие начального состояния систем;

г) подобие условий на границах систем в течение всего рассматриваемого периода процесса;

д) равенство определяющих критериев, при этом определяющими критериями подобия являются те, которые имеют существенное значение в изучаемом процессе.

При характеристике того или иного механического процесса механическое подобие может быть определено заданием переходных множителей или масштабов для длин (геометрическое подобие), для времени (кинематическое подобие) и для масс (динамическое подобие).

Для двух подобных систем условиегеометрического подобия состоит в том, что все размеры пространства, занятого системой в модели, и размеры отдельных элементов модели изменены в определенное число mL раз по сравнению с соответствующими размерами натуры:

Lм / Lн= mL, (10.1)

где Lм и Lн - соответственно линейные размеры модели и натуры.

Условие кинематического подобия этих систем состоит в том, что любые сходственные точки (частицы) систем, двигаясь по геометрически подобным траекториям, проходят геометрически подобные пути в промежутки времени Т, отличающиеся постоянным множителемmТ

Тм / Тн= mТ. (10.2)

Условие динамического подобия систем состоит в том, что массы любых сходственных частиц этих систем отличаются друг от друга постоянным множителемmМ

Мм / Мн= mМ.(10.3)

Особенности объектов геомеханики состоят в том, что при заданном геометрическом масштабе моделирования (mL = Lм / Lн) для обеспечения механического подобия модели и натуры необходимо отказаться в модели либо от равенства sм = sн, либо от равенства gм = gн, либо от равенства обоих показателей.

Если сохранить в модели равенство напряжений натуре (другими словами, равенство механических свойств материала модели и натуры), т.е. условие sм =sн, то необходимо обеспечить, чтобы объемный вес материала был больше в число раз, обратное геометрическому масштабу.

Например, при геометрическом масштабе модели mL = Lм / Lн = 1/100 объемный вес материала модели должен быть равен

Lн1

gм = --------- gн = --------- gн = 100gн.(10.4)

LмmL

Условие (10.4) можно выполнить, применив в модели натуральные горные породы и придав им фиктивный объемный вес (100gн в приведенном случае при mL = 1/100) с помощью инерционных сил, которые могут быть созданы, например, путем вращения модели в центрифуге при соответствующем значении центробежной силы. Этот метод был предложен в 1932 г. профессорами Г. И. Покровским и Н. Н. Давиденковым и носит название метода центробежного моделирования.

Если же в модели применить некоторые искусственные материалы, механические характеристики которых ниже соответствующих характеристик моделируемых горных пород, т. е. отказаться от равенства sм = sн, то для обеспечения условий механического подобия модели и натуры необходимо

Lмgм

sм = -------. -------sн.(10.5)

Lнgн

Искусственные материалы, соответствующие механические характеристики которых в принятом геометрическом масштабе моделирования удовлетворяют по отношению к моделируемым горным породам условию (10.5), называют материалами - эквивалентами данным горным породам или эквивалентными материалами.Метод же моделирования, основанный на применении эквивалентных материалов и предложенный в 1936 г. проф. Г. Н. Кузнецовым, носит название метода эквивалентных материалов.

При моделировании системы в соответствующем геометрическом масштабе продолжительность тех или иных процессов обычно изменяется. В связи с этим существенно важное значение имеет вопрос о масштабе времени при моделировании, который в общем случае определяется, исходя из приведенного выше условия кинематического подобия двух систем (10.2).

В тех случаях, когда на моделях воспроизводят сразу несколько процессов, масштабы времени для отдельных из них могут оказаться неодинаковыми В таких случаях масштаб времени устанавливают, исходя из соблюдения подобия в протекании лишь тех процессов, которые в решаемой задаче являются основными и не учитывают малозначащие элементы.

Нагружение физических моделей осуществляется:

* созданием усилий на контуре модели при помощи механических и гидравлических домкратов или заданием деформаций контура посредством жёстких ограничителей;

* собственным весом модели массива;

* посредством центробежных сил, возникающих в центрифуге;

* с помощью сил сопротивления сдвигу, как это делается в моделях с фрикционной базой.

1. Критерий подобия Нуссельта. Характеристика критерия.

В анализе систем, имеющих границы раздела фаз, появляются внутренние характерные масштабы, связанные с взаимодействием внешних полей и поверхностных эффектов. В газожидкостных потоках важнейшая характеристика этих эффектов – коэффициент поверхностного натяжения σ, Н/м. Основные гидродинамические взаимодействия поверхностного натяжения возникают с гравитационными силами, обусловленными разностью плотностей фаз (сила Архимеда), с мерой g(ρ’–ρ’’), Па/м, динамическим напором с мерой ρU2, Па, и вязким трением, мерой которого является динамическая вязкость μ, Па*с, или кинематическая вязкость ν, м2/с.
При наличии свободных границ возникают также локальные взаимодействия подъёмной (архимедовой) силы и вязкого трения. Из этих величин можно образовать несколько масштабов, существенных в анализе термогидродинамики газожидкостных систем.
Вводя в классические критерии подобия внутренние линейные масштабы, можно образовать новые критерии, не зависимые от внешних геометрических характеристик потока. Такую операцию проводят в теории пограничного слоя при образовании чисел Рейнольдса. Существенно, что в данном случае результат получается нетривиальным и приводит к качественно новым безразмерным параметрам.
Так, для гравитационно-вязкого течения жидкой плёнки число Нуссельта удобно писать в форме

Nu=(α/λ’)[ν’2ρ’/g(ρ’-ρ’’)]1/3 (2),

то есть строить его по внутреннему линейному масшабу.
Введя в число Нуссельта линейный масштаб капиллярно-гравитационного взаимодействия, получим ещё одну его форму

Nu=(α/λ’)[σ/g(ρ’-ρ’’)]1/2 (3)

1. Критерий подобия Рейнольдса. Характеристика критерия.

Критерии подобия, необходимые условия физического подобия двух явлений, например явлений, имеющих место для натурного объекта и его модели. Критерии подобия, состоящие в равенстве для рассматриваемых явлений некоторых безразмерных величин, называются характеристическими числами. Иногда критериями подобия называются сами эти числа. Ими являются число Маха, число Рейнольдса, число Прандтля, число Струхаля, число Эйлера, число Фруда и другие.

***

Число Рейнольдса – безразмерное соотношение, которое, как принято считать, определяет ламинарный или турбулентный режим течения жидкости или газа. Число Рейнольдса также считается критерием подобия потоков.

Число Рейнольдса определяется следующим соотношением:

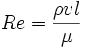
где ρ – плотность среды, v – характерная скорость, l – характерный размер, μ – динамическая вязкость среды.

Переход от ламинарного к турбулентному режиму происходит по достижении так называемого критического числа Рейнольдса Rekp. При Re < Rekp течение происходит в ламинарном режиме, при Re > Rekp возможно возникновение турбулентности. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.). Например, для течения в круглой трубе .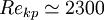

Число Рейнольдса как критерий перехода от ламинарного к турбулентному режиму течения и обратно относительно хорошо действует для напорных потоков. При переходе к безнапорным потокам переходная зона между ламинарным и турбулентным режимами возрастает, и использование числа Рейнольдса как критерия не всегда правомерно. Например, в водохранилищах формально вычисленные значения числа Рейнольдса очень велики, хотя там наблюдается ламинарное течение.

Критерий назван в честь выдающегося английского физика О. Рейнольдса (1842–1912), автора многочисленных пионерских работ по гидродинамике.

***

Критерий Рейнольдсa (критерий гидродинaмического подобия):

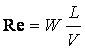
где W – скорость потока; L – определяющий размер; V – кинематическая вязкость среды.

***

Уравнение индукции магнитного поля имеет очень важную интерпретацию в магнитной гидродинамике. Действительно, отношение по порядку величины второго члена в правой стороне этого уравнения к первому равно

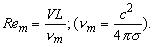
Здесь V – некоторая характерная скорость задачи (например, скорость невозмущенного потока, набегающего на обтекаемое тело), а L – характерный размер (например, размер обтекаемого тела). Величина nm называется магнитной вязкостью. Число Rem внешне похоже на число Рейнольдса в классической гидроаэромеханике (только вместо кинематической вязкости жидкости n = m /r в рассматриваемом случае в знаменателе стоит магнитная вязкость) и играет такую же важную роль, как и число Рейнольдса в гидроаэромеханике.

Предельные случаи:

Rem>>1

Rem<<1

В первом случае очень больших магнитных чисел Рейнольдса уравнение индукции магнитного поля можно записать в форме

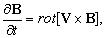
в которой пренебречь последним членом полного уравнения, представляющим собой диссипацию энергии вследствие протекания электрических токов. Из последнего уравнения видно, что движение электропроводных жидкостей и газов в случае Rem>>1 сильно влияет на распределение магнитного поля, а, следовательно, и на распределение всех остальных электродинамических величин. Кроме того, есть теорема, что поток соленоидального вектора, которым является магнитное поле (div B = 0), через некоторую поверхность S в жидкости, ограниченную жидким контуром С, остается со временем постоянным. Физически это означает, что никакая силовая линия магнитного поля во время движения не может покинуть поверхность S через контур С. Это свойство электропроводных жидкостей и газов в случае Rem>>1 называется условием «вмороженности» магнитных силовых линий в электропроводную среду. В гидроаэромеханике аналогом являются вихревые линии, которые при некоторых условиях могут быть «вморожены» в жидкость (одна из теорем Гельмгольца о вихрях). Случай Rem>>1 чаще всего осуществляется в различных физических проблемах, встречающихся в условиях космического пространства. Это связано с тем, что обычно в этих условиях характерные размеры L приводят к очень большим значениям магнитного числа Рейнольдса.

В качестве примера приведем обтекание магнитосферы Земли солнечным ветром. Скорость солнечного ветра в районе орбиты Земли равна, в среднем, V ~ 4•107см/сек, характерный размер обтекаемой магнитосферыL ~ 10RE ~ 6,4•109 см (RE – радиус Земли), nm ~ 106 см2/сек, т.е. Rem ~ 1011>>1. Таким образом, при обтекании Земли солнечным ветром осуществляется случай Rem>>1, т.е., в силу принципа «вмороженности», солнечный ветер не может проникнуть в магнитосферу Земли, а обтекает ее, поджимая магнитосферу с подветренной стороны и вытягивая ее в хвостовой части, как показано на рис. 1. На этом рисунке область «1» представляет собой невозмущенный солнечный ветер, Г – головная ударная волна, М – так называемая магнитопауза, отделяющая солнечный ветер за головной ударной волной от магнитосферы Земли, А – точка торможения солнечного ветра, в которой скорость равна нулю, область «2» заполнена солнечным ветром, параметры которого за ударной волной отличаются от параметров в области «1», область «3» – магнитосфера Земли, куда не проникает солнечный ветер. Исследования с помощью космических аппаратов обнаружили, что хвост магнитосферы Земли может вытягиваться вплоть до орбиты Луны.

Качественная картина обтекания магнитосферы Земли солнечным ветром

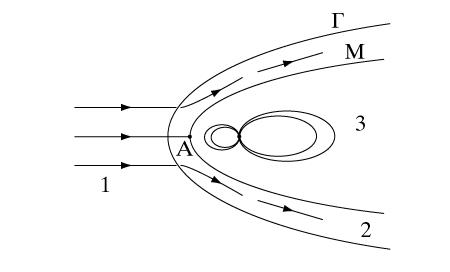
Рис. 1

В случае Rem<<1 уравнение индукции имеет вид

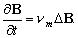
Из этого уравнения видно, что движение электропроводных жидкостей и газов не влияет на магнитное поле, а, следовательно, и на другие электродинамические величины. В этом случае малых магнитных чисел Рейнольдса, который обычно встречается в лабораторных условиях из-за небольших электропроводностей и малых характерных масштабов рассматриваемых проблем, электрическое и магнитное поля можно считать заданными величинами и не рассматривать законы индукции Фарадея. Математическая задача решения таких проблем, к которым относятся плазменные ускорители, магнитогидродинамические генераторы энергии, электромагнитные насосы для перекачки жидких металлов и т.п., существенно упрощается.

Принципиальная схема устройства магнитогидродинамического генератора электрической энергии

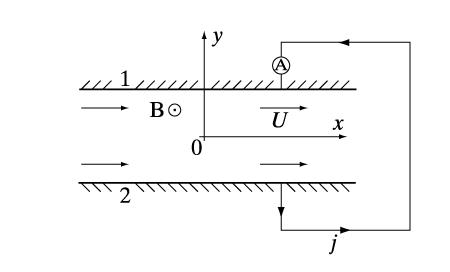
Рис. 2

В качестве примера рассмотрим основной принцип устройства магнитогидродинамического генератора. По каналу, например, прямоугольного сечения вдоль оси Оx пропускается электропроводная жидкость со скоростью U в магнитном поле B, направленном вдоль оси Oz, перпендикулярной плоскости чертежа (смотрите рис. 2). Тогда, в силу обобщенного закона Ома, перпендикулярно скорости течения и магнитному полю (эффективное электрическое поле равно 1/c VґB) вдоль оси Oy потечет электрический ток. Если бы стенки канала 1 и 2 были диэлектриками, то возникло бы электрическое поле Е, которое привело бы к запиранию тока (Е = –1/c VґB, т.е. j = 0). Однако, если 1 и 2 являются электродами, то по показанной на рисунке 2 замкнутой электрической цепи потечет ток, который может быть измерен амперметром А. На таком принципе и устроены магнитогидродинамические генераторы. При этом массовая сила в уравнении движения, пропорциональная векторному произведению jґB, направлена противоположно скорости и будет тормозить поток.

Можно видеть, что при внешнем воздействии электрического поля, перпендикулярного внешнему приложенному магнитному полю, можно добиться, чтобы сила 1/c jґB действовала вдоль направления скорости. На таком принципе основаны плазменные ускорители.

1. Критерий Грасгофа. Характеристика критерия.

Число Грасгофа — критерий подобия определяющий перенос тепла при конвективном теплообмене для случая свободной конвекции, когда движение вызывается разностью плотностей из-за неравномерности поля температур вблизи нагретого тела:

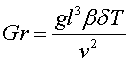
где g — ускорение свободного падения, I характерный размер, v - кооэфициент кинематической вязкости, β — коэффициент объемного расширения, δT — разница температур между поверхностью тела и средой.Число Грасгофа является произведением числа

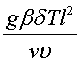
характеризующего отношение силы трения к подъёмной силе (архимедовой) (число Архимеда), на число Рейнольдса.

Теплоотдача в условиях свободной конвекции определяется зависимостью Nu = f(Gr, Рr), где Nu число Нуссельта, Pr— число Прандтля. Для газов и неметаллических жидкостей (при Рr> 0.7) в этом равенстве аргументом является произведение Gr*Pr, называемое числом Рэлея Ra. Для определения зависимости Nu = f(Gr, Рr) предложено много эмпирических корреляционных формул: большинство из них имеет вид зависимости

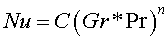
При Pr<< 1 (расплавленные металлы) формулу для определения теплоотдачи представляют в виде Nu=φ(Gr*Pr2) и часто пользуются соотношением

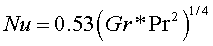
Параметр Gr в условиях свободной конвекции играет роль, аналогичную числу Re при вынужденных течениях. Аналогично критическому числу Reкр, критическое число Gr определяет переход от ламинарного режиматечения к турбулентному в условиях свободной конвекции.

1. Критерии подобия Прандтля. Характеристика критерия.

Критерии подобия, необходимые условия физического подобия двух явлений, например явлений, имеющих место для натурного объекта и его модели. Критерии подобия, состоящие в равенстве для рассматриваемых явлений некоторых безразмерных величин, называются характеристическими числами. Иногда критериями подобия называются сами эти числа. Ими являются число Маха, число Рейнольдса, число Прандтля, число Струхаля, число Эйлера, число Фруда и другие.

Число Прандтля (Pr) [Prandtl number] – критерий подобия, характеризующий соотношение между интенсивностью молекул, переноса механического импульса и интенсивностью переноса теплоты за счет теплопроводности в жидкостях и газах; численно равен отношению кинематического коэффициента вязкости к коэффициенту температуропроводности жидкости или газа (Рг = v/a).

Число Прандтля – один из критериев подобия тепловых процессов в жидкостях и газах:

Pr = n/a = mcp/l

где n = m/r – кинематическая вязкость; m – динамическая вязкость; r – плотность; l – теплопроводность; а = l/rcp – температуропроводность; cp – удельная изобарная среды при постоянном давлении. Названо по имени Л. Прандтля.

Теория подобия – учение об условиях подобия различных объектов (физических явлений, процессов, аппаратов, систем), отличающихся масштабами, геометрией или физической природой. Основные задачи теории подобия: установление критериев подобия разных объектов, изучение их свойств с помощью этих критериев, определение возможности обобщения результатов решения конкретных задач при отсутствии способов нахождения их полных решений. Успехи в развитии теории связаны с именами И. Ньютона, Ж. Фурье, Дж. Рэлея, T. Афанасьевой–Эренфест, M. Рябушинского, P. Бэкингема, П. Бриджмена, M. В. Кирпичева, А. А. Гухмана, Г. К. Дьяконова, Л. И. Седова и др.

Два объекта подобны, если в соответствующие (сходственные) моменты времени в соответствующих точках пространства значения переменных величин, характеризующих состояние одного объекта, пропорциональны значениям соответствующих величин другого объекта. Коэффициент пропорциональности соответствующих величин называются коэффициентами подобия.

Виды подобия.
Различают геометрическое, физическое, физико–химическое и математическое подобие. При геометрическом подобии пропорциональны геометрические характеристики соответствующих элементов объектов (например, длины, высоты или диаметры аппаратов). При физическом подобии в пространстве и времени подобны поля соответствующих физических параметров двух объектов, например, при кинематическом подобии – поля скоростей, при динамическом подобии – системы действующих сил или силовых полей (силы инерции, тяжести, вязкости, давления); при механическом или гидромеханическом подобии, предполагающем наличие геометрического, кинематического и динамического подобия, – упругие системы, потоки жидкостей, газов или их смесей; при подобии тепловых процессов – соответствующие поля температур и тепловых потоков; при подобии массообменных процессов – потоки веществ и поля их концентраций; при подобии химических процессов – поля концентраций, температур; при электродинамическом подобии – поля токов, нагрузок, мощностей, электромагнитных сил. Для сложных физических и физико–химических процессов, включающих механические, гидромеханические, тепло– и массообменные, а также химические явления, теория подобия устанавливает условия подобия, например процессов трения при движении материальных потоков в трубах, каналах и аппаратах, кинетики физико–химических превращений и других явлений. При математическом подобии рассматриваемые объекты описываются одинаковыми уравнениями, что позволяет говорить, например, о подобии тепловых и массообменных процессов.

Число Прандтля:

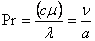
где ν – кинематическая вязкость; a – коэффициент температуропроводности.

Физический смысл: мера соотношения вязкостных и температуропроводных свойств теплоносителей; мера соотношения полей скоростей и температур в потоке.

Существует и другое Число Прандтля*, которое в зарубежной литературе называется числом Шмидта (Sc):

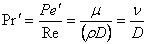
где ν – кинематическая вязкость; D – коэффициент диффузии.

Физический смысл: Мера постоянства соотношений физических свойств жидкостей (газов) в подобных потоках; мера подобия профилей скоростей и концентраций в процессах массоотдачи.

Число Прандтля – безразмерная величина, определяющая процессы теплопередачи в движущихся жидкостях и газах; является критерием подобия двух неизотермических потоков жидкости (газа). Названо по имени Л. Прандтля.

Теория подобия – учение об условиях подобия физических явлений. Теория подобия основана на учении о размерностях физических величин и служит основой моделирования. Теория подобия устанавливает критерии подобия различных физических явлений, позволяющие с их помощью изучать свойства самих явлений. Явные и неявные функциональные связи между критериями подобия, которые получают с помощью теории подобия (так называемые критериальные зависимости) способствуют пониманию сложных физических процессов и помогают интерпретировать результаты как экспериментальных исследований, так и числовых расчётов, объём которых прогрессивно возрастает по мере развития численных методов и совершенствования электронно–вычислительной машины. Теория подобия, дозволяет формулировать физические закономерности и извлекать идеи из огромной массы расчётных или экспериментальных результатов.

Физические явления, процессы или системы подобны, если в сходственные моменты времени в сходственных точках пространства значения переменных величин, характеризующих состояние одной системы, пропорциональной соответствующим величинам другой системы. Физическое подобие является обобщением элементарного и наглядного понятия геометрического подобия, при котором существует пропорциональность (подобие) сходственных геометрических элементов подобных фигур или тел. При физическом подобии поля соответствующих (одноимённых) параметров двух систем подобны в пространстве во времени. Например, при кинематическом подобии существует подобие полей скорости для двух рассматриваемых движений; при динамическом подобии реализуется подобие систем действующих сил или силовых полей различной физической природы (сил тяжести, сил давления, сил вязкости и); механическое подобие (подобие двух потоков жидкости или газа, подобие двух упругих систем) предполагает наличие геометрического, кинематического и динамического подобий; при подобии тепловых процессов подобны соответствующие поля температур и тепловых потоков, при электродинамическом подобии – поля токов, нагрузок, мощностей, электро–магнитных сил. Все перечисленные виды подобия – частные случаи физического подобия.

Безразмерные величины, производные физической величины, не зависящие от изменения в одно и то же число раз величин, выбранных за основные. Если, например, за основные величины выбраны длина L, масса М и время Т и их изменения в одно и то же число раз не влияют на размер данной величины, то размерность такой величины равна L°M°T° = 1, и она в этой системе величин является безразмерной. Например, плоский угол, определяемый как отношение длины дуги окружности, заключённой между двумя радиусами, к длине радиуса, в системе LMT является безразмерной величиной, так как не зависит от длины радиуса. К безразмерным величинам относятся также все относительные величины: относительная плотность (плотность тела по отношению к плотности воды), относительное удлинение, относительные магнитная и диэлектрическая проницаемости, а также критерии подобия (числа Рейнольдса, Прандтля и другие). Безразмерные величины выражаются в отвлечённых единицах. Относительные величины выражаются также в процентах (%) и промилле (°/оо).

1. Метод аналогий.

Под аналогией понимается подобие, сходство каких-то свойств, признаков или отношений у различных в целом объектов. Уста­новление сходства (или различия) между объектами осуществля­ется в результате их сравнения. Таким образом, сравнение ле­жит в основе метода аналогии.

Если делается логический вывод о наличии какого-либо свой­ства, признака, отношения у изучаемого объекта на основании установления его сходства с другими объектами, то этот вывод называют умозаключением по аналогии.

Степень вероятности получения правильного умозаключения по аналогии будет тем выше: 1) чем больше известно общих свойств у сравниваемых объектов; 2) чем существеннее обнару­женные у них общие свойства и 3) чем глубже познана взаим­ная закономерная связь этих сходных свойств. При этом нужно иметь в виду, что если объект, в отношении которого делается умозаключение по аналогии с другим объектом, обладает ка­ким-нибудь свойством, не совместимым с тем свойством, о су­ществовании которого должен быть сделан вывод, то общее сход­ство этих объектов утрачивает всякое значение.

Метод аналогии применяется в самых различных областях науки: в математике, физике, химии, кибернетике, в гумани­тарных дисциплинах и т. д. О познавательной ценности метода аналогии хорошо сказал известный ученый-энергетик В. А. Ве­ников: «Иногда говорят: «Аналогия — не доказательство».Новедь если разобраться, можно легко понять, что ученые и не стре­мятся только таким путем доказать что-нибудь. Разве мало того, что верно увиденное сходство дает могучий импульс творчеству? Аналогия способна скачком выводить мысль на новые, неизве­данные орбиты, и, безусловно, правильно положение о том, что аналогия, если обращаться с ней с должной осторожностью, — наиболее простой и понятный путь от старого к новому»].

Существуют различные типы выводов по аналогии. Но об­щим для них является то, что во всех случаях непосредственно­му исследованию подвергается один объект, а вывод делается о другом объекте. Поэтому вывод по аналогии в самом общем смысле можно определить как перенос информации с одного объекта на другой. При этом первый объект, который собствен­но и подвергается исследованию, именуется моделью, а другой объект, на который переносится информация, полученная в ре­зультате исследования первого объекта (модели), называется ори­гиналом (иногда — прототипом, образцом и т. д.). Таким образом, модель всегда выступает как аналогия, т. е. модель и ото­бражаемый с ее помощью объект (оригинал) находятся в опре­деленном сходстве (подобии).

«.Под моделированием понимается изучение моделируемо­го объекта (оригинала), базирующееся на взаимооднозначном соответствии определенной части свойств оригинала и замещающего его при исследовании объекта (модели) и включающее в себя построение модели, изучение ее и перенос полученных све­дений на моделируемый объект — оригинал»[39].

Использование моделирования диктуется необходимостью раск­рыть такие стороны объектов, которые либо невозможно постиг­нуть путем непосредственного изучения, либо невыгодно изучать их таким образом из чисто экономических соображений. Человек, например, не может непосредственно наблюдать процесс естест­венного образования алмазов, зарождения и развития жизни на Земле, целый ряд явлений микро- и мегамира. Поэтому прихо­дится прибегать к искусственному воспроизведению подобных явлений в форме, удобной для наблюдения и изучения. В ряде же случаев бывает гораздо выгоднее и экономичнее вместо непосред­ственного экспериментирования с объектом построить и изучить его модель.

В зависимости от характера используемых в научном иссле­довании моделей различают несколько видов моделирования.

1. Мысленное (идеальное) моделирование. К этому виду мо­делирования относятся различные мысленные представления в форме тех или иных воображаемых моделей. Сле­дует заметить, что мысленные (идеальные) модели нередко могут быть реализованы материально в виде чувственно вос­принимаемых физических моделей.

2. Физическое моделирование. Оно характеризуется физи­ческим подобием между моделью и оригиналом и имеет целью воспроизведение в модели процессов, свойственных оригиналу. По результатам исследования тех или иных физических свойств модели судят о явлениях, происходящих (или могущих про­изойти) в так называемых «натуральных условиях».

В настоящее время физическое моделирование широко ис­пользуется для разработки и экспериментального изучения раз­личных сооружений, машин, для лучшего понимания каких-то природных явлений, для изучения эффективных и безопасных способов ведения горных работ и т. д.

3. Символическое (знаковое) моделирование. Оно связано с условно-знаковым представлением каких-то свойств, отношений объекта-оригинала. К символическим (знаковым) моделям от­носятся разнообразные топологические и графовые представле­ния (в виде графиков, номограмм, схем и т. п.) исследуемых объектов или, например, модели, представленные в виде хими­ческой символики и отражающие состояние или соотношение элементов во время химических реакций.

Особой и очень важной разновидностью символического (зна­кового) моделирования является математическое моделирова­ние. Символический язык математики позволяет выражать свой­ства, стороны, отношения объектов и явлений самой различной природы. Взаимосвязи между различными величинами, описы­вающими функционирование такого объекта или явления, мо­гут быть представлены соответствующими уравнениями (диф­ференциальными, интегральными, интегро-дифференциальными, алгебраическими) и их системами.

4. Численное моделирование на компьютере. Эта разновид­ность моделирования основывается на ранее созданной матема­тической модели изучаемого объекта или явления и применя­ется в случаях больших объемов вычислений, необходимых для исследования данной модели.

Численное моделирование особенно важно там, где не совсем ясна физическая картина изучаемого явления, не познан внут­ренний механизм взаимодействия. Путем расчетов на компью­тере различных вариантов ведется накопление фактов, что дает возможность, в конечном счете, произвести отбор наиболее ре­альных и вероятных ситуаций. Активное использование мето­дов численного моделирования позволяет резко сократить сро­ки научных и конструкторских разработок.

Метод моделирования непрерывно развивается: на смену од­ним типам моделей по мере прогресса науки приходят другие. В то же время неизменным остается одно: важность, актуаль­ность, а иногда и незаменимость моделирования как метода научного познания.

Дата добавления: 2015-05-26