Теория тепломассообмена. 1 страница

1. Теплопроводность. Закон Фурье.

Теплопроводность – один из видов переноса теплоты от более нагретых частей тела к менее нагретым, приводящий к выравниванию температуры. При теплопроводности перенос энергии осуществляется в результате непосредственной передачи энергии от частиц (молекул, атомов, электронов), обладающих большей энергией, частицам с меньшей энергией.

К выводу уравнения теплопроводности

Рис. 1

Рассмотрим процесс переноса. Пусть G – величина, характеризующая некоторое молекулярное свойство, отнесенное к одной молекуле. Если в равновесном состоянии распределение G равномерно по объему, то при наличии градиента G имеет место движение G в направлении его уменьшения. Пусть ось X направлена вдоль градиента G (рис. 1). Пусть имеется площадка dS, которую пересекают молекулы, пришедшие со всевозможных направлений и пересекающие ее в направлении отрицательных значений оси X. Среднее расстояние по оси X, на котором испытали последнее столкновение молекулы, пересекшие площадку dS, не равно среднему свободному пробегу, а составляет 2/3 от него: , где – средняя длина свободного пробега молекулы. Эта величина в большинстве случаев мала, и G можно представить на расстоянии в виде разложения Тейлора

Поток числа молекул в направлении оси X равен , где n0 – концентрация молекул, – средняя скорость теплового движения. Следовательно, поток G сквозь площадку dS в направлении отрицательных значений оси X равен

,

а в направлении положительных значений

,

отсюда полный поток через площадку:

.

В случае теплопроводности G есть средняя энергия теплового движения, приходящаяся на одну молекулу. Из теоремы о равнораспределении энергии по степеням свободы имеем

.

Тогда уравнение переноса принимает вид:

, (1)

где

– коэффициент теплопроводности, ρ – плотность, cV – удельная теплоемкость. Уравнение (1) называется законом Фурье для теплопроводности.

Учение о теплопроводности начало развиваться во второй половине XVIII в. и получило завершение в работах Ж.Б.Ж.Фурье, опубликовавшего в 1822 г. монографию «Аналитическая теория теплоты».

Поскольку = 1/σ, где σ – поперечное сечение, не зависит от давления, а и также не зависит от давления, то можно заключить, что теплопроводность не зависит от давления и увеличивается приблизительно прямо пропорционально корню квадратному из температуры. Приблизительно потому, что с увеличением температуры σ несколько уменьшается по закону, зависящему от характера взаимодействия между молекулами. Для многоатомных газов необходимо также учесть возрастание теплоемкости CV c температурой.

1. Виды и режимы теплообмена.

Существуют три основных вида теплопередачи: теплопроводность, конвекция и лучистый теплообмен.

Теплопроводность. Если внутри тела имеется разность температур, то тепловая энергия переходит от более горячей его части к более холодной. Такой вид теплопередачи, обусловленный тепловыми движениями и столкновениями молекул, называется теплопроводностью; при достаточно высоких температурах в твердых телах его можно наблюдать визуально. Так, при нагревании стального стержня с одного конца в пламени газовой горелки тепловая энергия передается по стержню, и на некоторое расстояние от нагреваемого конца распространяется свечение (с удалением от места нагрева все менее интенсивное).

Интенсивность теплопередачи за счет теплопроводности зависит от градиента температуры, т.е. отношения DТ/Dx разности температур на концах стержня к расстоянию между ними. Она зависит также от площади поперечного сечения стержня (в м2) и коэффициента теплопроводности материала [в соответствующих единицах Вт/(мDК)]. Соотношение между этими величинами было выведено французским математиком Ж.Фурье и имеет следующий вид:

где q – тепловой поток, k – коэффициент теплопроводности, а A – площадь поперечного сечения. Это соотношение называется законом теплопроводности Фурье; знак «минус» в нем указывает на то, что теплота передается в направлении, обратном градиенту температуры.

Из закона Фурье следует, что тепловой поток можно понизить, уменьшив одну из величин – коэффициент теплопроводности, площадь или градиент температуры. Для здания в зимних условиях последние величины практически постоянны, а поэтому для поддержания в помещении нужной температуры остается уменьшать теплопроводность стен, т.е. улучшать их теплоизоляцию.

1. Стационарная теплопроводность.

В стационарном режиме теплопроводности температурное поле не изменяется во времени, т.е. . В этом случае дифференциальное уравнение теплопроводности для тел простейшей формы при допущении независимости физических свойств тела от температуры принимает вид

или в дивергентной форме ,

где x1 – координата, м; k – коэффициент формы тела. Подставляя в последнее уравнение значения коэффициента формы тела и обозначение координаты для тел простейшей формы, получим

а) бесконечная пластина или плоская стенка (k = 1, x1 = x)

;

б) бесконечный цилиндр (k = 2, x1 = r)

или в дивергентной форме ;

в) шар или сфера (k = 3, x1 = r) или в дивергентной форме .

Плоская стенка

Решим дифференциальное уравнение теплопроводности для плоской стенки при следующих условиях однозначности:

— толщина стенки равна δ, м;

— коэффициент теплопроводности стенки не зависит от температуры и равен λ Вт/(м·К);

— внутренние источники (стоки) теплоты в стенке отсутствуют, т.е. ;

— на обеих поверхностях плоской стенки задано значение температуры (ГУ I рода)

.

Рис.2.4. Стационарное температурное поле в плоской стенке

Решение дифференциального уравнения для бесконечной пластины выполним двойным интегрированием:

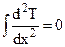откуда следует .

И окончательно получаем общее решение температурного поля в виде

,

из анализа, которого следует, что в плоской стенке при стационарном режиме теплопроводности температура линейно изменяется по ее толщине (см. рис.2.4.).

Постоянные интегрирования находим, используя граничные условия путем решения системы из двух линейных уравнений

.

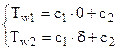Из первого уравнения следует, что , а из второго уравнения системы находим постоянную

.

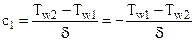Подставляя значение постоянных интегрирования в общее решение, окончательно получаем

.

Зная температурное поле, несложно рассчитать плотность теплового потока в плоской стенке, воспользовавшись законом Фурье

или ,

где – тепловая проводимость плоской стенки, Вт/(м2×К); – термическое сопротивление теплопроводности плоской стенки, (м2×К)/Вт.

Из анализа формулы для расчета плотности теплового потока следует, что тепловой поток не изменяется по толщине плоской стенки или в любой точке плоской стенки. Поэтому для любого i-го слоя многослойной стенки можно записать

,

где 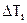– перепад температур на i-ом слое многослойной стенки; – термическое сопротивление теплопроводности i-го слоя многослойной стенки.

Из последнего выражения следует, что перепад температур на каждом слое многослойной стенки прямо пропорционален термическому сопротивлению этого слоя

Плотность теплового потока для плоской стенки, состоящей из n слоев, рассчитывается по формуле:

.

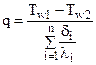1. Теплопроводность через различные виды стенок.

Чтобы понять, как считать теплопроводность - необходимо представить материал в виде вымышленной стены. На практике такие стены будут реальными. Данная статья поможет нам рассчитать теплопотери стены. Сложив все теплопотери стнен - получим теплопотери всего дома. Но это только один фактор из трех составляющих теплопотерь дома. Не забывайте про вентиляцию и излучение тепла. О них поговорим в других статьях.

Также решим задачку для реального события. Смотри ниже.

Смотри изображение:

t1, t2 - точки температур. L - толщина стены. S - площадь стены.

Теплопроводность представляет собой количество теплоты, которое проходит в единицу времени через единицу толщины слоя материала.

Если быть точнее! То это отношение поверхностной плотности теплового потока к температурному градиенту.

Температурный градиент - это произведение толщины стенки материала на разность температур между противоположными плоскостями одной стенки.

Температурный градиент = L х (t1 - t2).

Плотность теплового потока - это количество теплоты в единицу времени. Количество теплоты измеряется в Калориях. О калориях поговорим ниже.

Сначала я Вам покажу формулу нахождения теплопроводности и связи между ними.

λ - Коэффициент теплопроводности.

t1,t2 - температуры стенки по разные стороны. Измеряется либо в Цельсиях [°C] либо в Кельвинах [K].

°С = K - 273,15

Из-за того, что температура измеряется в разных единицах, то коэффициент теплопроводности, тоже имеет различные единицы измерения:

[ Вт / (м•°С) ] либо [ Вт / (м•K) ]

В редких случаях за место (Вт) может использоваться (Калория).

L - Толщина стенки, измеряется в метрах(м).

Q - Количество теплоты, измеряется в калориях(K) или в ваттах(Вт).

Эталоном значения одной калории является: Количество теплоты необходимое для того, чтобы нагреть один грамм воды на 1 градус Цельсия или Кельвина, при атмосферном давлении (101325 Па).

1 Дж = 0,2388 калорий 1000 Калорий = 1 кКалория = 1,163 Ватт • час 1 Калория = 4,1868 Дж

Для глубокого понимания коэффициента теплопроводности, нужно понимать, как находят количество теплоты. То есть нам нужно найти количество теплоты, которое расходуется между наружными плоскостями одной стены. Мы фактически находим потерянное тепло через стену.

Можно представить тепло как некую жидкость, проходящую в сквозь стенку. И количество этой некой тепловой жидкости проходящей в единицу времени и будет являться той самой теплотой. Чем больше ее проходит, тем больше мы теряем тепло и тем больше теплопроводность. Теплоизоляторы понижают теплопроводность, и мы теряем меньше тепла.

Данная формула помогает нам найти проходящее количество теплоты в сквозь стену.

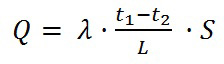
Также еще выражаются в такой форме:

R - Температурное сопротивление, измеряется: (м2 • °С) / Вт, или: (м2 • K) / Вт

Q - Количество теплоты. Измеряется в Ваттах (Вт) или Калориях (К)

t1,t2 - температура стенки по разные стороны. Измеряется либо в Цельсиях [°C] либо в Кельвинах [K].

S - площадь стенки, измеряется в квадратных метрах (м2). Площадь находится умножением высоты на длину стенки. S = a • b.

1. Нестационарная теплопроводность.

Процессы теплопроводности, в которых температурное по­ле тела изменяется не только в пространстве, но и во времени называются нестационарными.

Нестационарные процессы теплопроводности наблюдаются при нагревании или охлаждении различных заготовок и изделий, при пуске и останове различных теплообменных устройств, при изме­нении нагрузки теплообменник аппаратов и т.д.

Решить задачу нестационарной теплопроводности - это зна­чит найти зависимость изменения температурного поля от коор­динат и времениt=f1(х,у,z,t)

определить количество отведенной или подведенной к телу теплоты, Q=f2(х,у,z,t)

1.Определение количества теплоты, отдаваемой пластикой в процессе охлаждения

Количество теплоты, которое отдает или воспринимает пластина обеими поверхностями за время от Т == 0 до t=¥,

равно изменению внутренней энергии этой пластины за период полного ее охлаждения или нагревания

Здесь 2df=V - объем пластины;

2dfr=M - масса пластины^

Количество теплоты, отданной или воспринятой пластиной за время от Т == 0 до Т=Т1определяется как поля от пол­ного количества теплоты

где 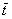- средняя температура пластины е момент времени — — 0^ "

Прибавим и вычтем tж:

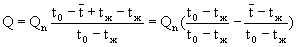
отсюда (1)

где 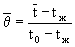- средняя безразмерная температура по толщине пластины в момент времени Т.Из уравнения (1) видно, что определение количества теплоты, отданной или воспринятой пластиной, сводится к на­хождению средней безразмерной температуры .Для этого используем теорем о среднем:

Подставив значение q и проинтегрировав в указанных пределах, получим

При значениях критерия F0³ 0,3 для пластины можно огра­ничиться первым членом суммы:

В полученной форуле первый множитель зависит только от критерияBi и может быть представлен как. некоторая фикция М(Bi), котрая может быть заранее подсчи­тана. В этом случае расчет будет сводиться к вычислению экспоненты

1. Основной закон Стефана-Больцмена при излучении.

Закон Стефана-Больцмана — Энергетическая светимость абсолютно черного тела пропорциональна четвертой степени абсолютной температуры.

Из формулы видно, что при повышении температуры светимость тела не просто возрастает — она возрастает в значительно большей степени. Увеличьте температуру вдвое, и светимость возрастет в 16 раз!

Нагретые тела излучают энергию в виде электромагнитных волн различной длины. Когда мы говорим, что тело «раскалено докрасна», это значит, что его температура достаточно высока, чтобы тепловое излучение происходило в видимой, световой части спектра. На атомарном уровне излучение становится следствием испускания фотонов возбужденными атомами.

Чтобы понять, как действует этот закон, представьте себе атом, излучающий свет в недрах Солнца. Свет тут же поглощается другим атомом, излучается им повторно — и таким образом передается по цепочке от атома к атому, благодаря чему вся система находится в состоянии энергетического равновесия. В равновесном состоянии свет строго определенной частоты поглощается одним атомом в одном месте одновременно с испусканием света той же частоты другим атомом в другом месте. В результате интенсивность света каждой длины волны спектра остается неизменной.

Температура внутри Солнца падает по мере удаления от его центра. Поэтому, по мере движения по направлению к поверхности, спектр светового излучения оказывается соответствующим более высоким температурам, чем температура окружающий среды. В результате, при повторном излучении, согласно закону Стефана—Больцмана, оно будет происходить на более низких энергиях и частотах, но при этом, в силу закона сохранения энергии, будет излучаться большее число фотонов. Таким образом, к моменту достижения им поверхности спектральное распределение будет соответствовать температуре поверхности Солнца (около 5 800 К), а не температуре в центре Солнца (около 15 000 000 К).

Энергия, поступившая к поверхности Солнца (или к поверхности любого горячего объекта), покидает его в виде излучения. Закон Стефана—Больцмана как раз и говорит нам, какова излученная энергия.

В вышеприведенной формулировке закон Стефана—Больцмана распространяется только на абсолютно черное тело, поглощающее всё попадающее на его поверхность излучение. Реальные физические тела поглощают лишь часть лучевой энергии, а оставшаяся часть ими отражается, однако закономерность, согласно которой удельная мощность излучения с их поверхности пропорциональна Т в 4, как правило, сохраняется и в этом случае, однако постоянную Больцмана в этом случае приходится заменять на другой коэффициент, который будет отражать свойства реального физического тела. Такие константы обычно определяются экспериментальным путем.

В формуле мы использовали:

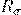— Энергетическая светимость тела

— Постоянная Стефана-Больцмана

— Абсолютная температура

1. Закон Ньютона и коэффициент теплоотдачи.

В практических инженерных расчетах теплоотдачу, т.е. теплообмен между поверхностью твердого тела и движущейся средой, сопри­касающейся с этой поверхностью, описывают законом Ньютона-Рихмана (20).

Согласно закону Ньютона-Рихмана тепловой поток Q от жидкости к стенке или от стенки к жидкости пропорционален поверхности теплообмена F и разности температур ∆t=(tc-tж) жидкости и стенки:

, [Вт] (114)

Разность температур (tc-tж) или (tж- tc) называют температурном напором.

Уравнение Ньютона-Рихмана для всего тепла Qτ, передаваемого за время τ запишется:

, (115)

для плотности теплового потока:

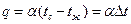, (116)

Уравнения (113)- (115) записаны для случая tc> tж. Если tж< tc, то в эти уравнения нужно записать tж - tc.

Коэффициент пропорциональности α, входящий в уравнение Ньютона-Рихмана, называется коэффициентом теплоотдачи. Он учитыва­ет конкретные условия процесса теплоотдачи, влияющие на его интен­сивность и имеет размерность:[α]=Вт/м2*К

Коэффициент теплоотдачи α характеризует интенсивность теп­лообмена на границе жидкость - стенка и численно равен количеству тепла, переданного в единицу времени через единицу поверхности, при разности температур между поверхностью и жидкостью в один градус. Коэффициент теплоотдачи α в отличие от коэффициента тепло­проводности λ не является физическим параметром среды и зависит от многих факторов.

В общем случае коэффициент теплоотдачи может изменяться по поверхности теплообмена, и поэтому различают средний по поверхности и локальный илиместный коэффициент теплоотдачи. Поэтому в общем случае с учетом переменности по поверхности уравнение Ньютона-Рихмана запишется:

,

отсюда

Последнее тождество можно рассматривать как определение α: коэффициент теплоотдачи есть плотность теплового потока на границе жидкость - стенка, отнесенная к разности температур стенки и жидкости. В соответствии с сказанным в уравнениях (113)-(115) под α следует понимать его среднее значение.

Применение формулы Ньютона-Рихмана никаких принципиальных упрощений для расчета конвективной теплоотдачи не дает. Вся слож­ность расчета в этом случае переносится на определение коэффициента теплоотдачи, т.е. простота формулы (113)-(115) является лишь кажущейся. В общем случае является функцией многих величин:

Т.е. в общем случае α является функцией скорости движения жид­кости, режима движения, физических параметров жидкости, температуры жидкости и тела, формы и размеров омываемого тела и т.д.

Инженерное решение задач конвективного теплообмена сводится чаще всего к определению α и вычислению количества переданной теплоты по формулам (2.127)-(2.129). Так как определить коэффициент теплоотдачи путем аналитического решения, приведенной в предыдущем параграфе, системы дифференциальных уравнений достаточно сложно, а в некоторых случаях и вообще невозможно, то для расчета α применяют теорию подобия.

1. Теплообмен между серыми телами в лучепрозрачной среде.

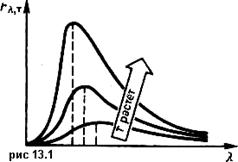
При рассмотрении теплообмена в системе твердых тел считаем заданными температуры этих тел, а искомыми — результирующие тепловые потоки, т. е. тепло, поглощаемое или излучаемое телами за единицу времени в результате теплообмена. Все тела считаем серыми, однако в пределе они могут быть и абсолютно черными (ε=1,0).

Для определения результирующего теплового потока i-того тела Qi в системе из n тел необходимо решить систему уравнений

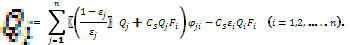(13.5)

Вместо одного из уравнений можно использовать уравнение теплового баланса

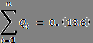
Для тел, поглощающих тепло, результирующий тепловой поток имеет положительное значение, для тел, отдающих тепло, — отрицательное.

В случае замкнутой системы из двух твердых тел, разделенных лучепрозрачной средой, решение системы уравнений (13.5) для тела 1имеет вид

Q1=Cпр(θ12-θ11)F11 (13.7)

где Cпр — приведенный коэффициент излучения системы, Вт/(м²*К4), определяется по формуле

(13.8)

где — приведенная степень черноты системы.

Для тел с высокой степенью черноты при практических расчетах можно использовать упрощенное выражение для приведенного коэффициента излучения системы

Cпр=CSε1ε2 (13.9)

Если в теплообмене двух тел участвует третье тело, являющееся адиабатным, для которого результирующий поток равен нулю (например, огнеупорная футеровка), причем все три тела образуют замкнутую систему, то результирующий тепловой поток также можно определить по формуле (13.7), а приведенный коэффициент излучения системы — по (13.8), заменяя значения угловых коэффициентов излучения φji на φобщ ji

Угловой коэффициент излучения φобщ ji учитывает отражение тепла от адиабатной поверхности и в общем случае может быть рассчитан по формуле

(13.10)

где k— адиабатное тело.

1. Излучение и поглощение в газах. Коэффициенты излучения некоторых тел и газов.

Каждое тело (Твердое, жидкое и газообразное) испускает тепловые лучи определенной волны. Эти лучи, уходя от одного тела, поглощаются другим телом, и принимают тепло на себя. И я попытаюсь Вам объяснить, как это происходит, и сколько тепла мы теряем этим излучением у себя дома на отопление. (Я думаю, многим будет интересно увидеть эти цифры). В конце статьи решим задачку из реального примера.

В статье будут трехэтажные формулы и интегральные выражения для математиков, но не стоит их бояться, можете даже не вникать в эти формулы. В задаче я вам дам формулы, которые решаются на-раз-два и даже не нужно знать высшую математику, достаточно знать элементарную арифметику.

Я не однократно в этом убеждался, что сидя у костра (обычно большого) мое лицо обжигали эти лучи. И если я закрывал костер своими ладонями и при этом руки были вытянуты, то получалось, что мое лицо переставало обжигать. Не трудно догадаться, что эти лучи прямые как световые. Меня обжигает не воздух, циркулирующий вокруг костра, и даже не теплопроводность воздуха, а именно прямые не видимые тепловые лучи, идущие от костра.

В космосе между планетами обычно вакуум и поэтому передача температур осуществляется исключительно тепловыми лучами (Все лучи - это электромагнитные волны).

Тепловое излучение имеет природу такую, как световые и электромагнитные лучи (волны). Просто, эти волны (лучи) имеют разную длину волны.

Например, длины волн в диапазоне 0,76 – 50 мкм, называется инфракрасными. Все тела, имеющие комнатную температуру + 20 °С, излучают в основном инфракрасные волны с длинами волн, близкими к 10 мкм.

Всякое тело, если только температура его отлична от абсолютного нуля (-273,15 °С), способно посылать в окружающее пространство излучение. Поэтому любое тело излучает на окружающие его тела лучи и в свою очередь находится под воздействием излучения этих тел.

Любая мебель в доме (стул, стол, стены и даже диван) испускает тепловые лучи.

Тепловое излучение может поглощаться или проходить в сквозь тело, а также может просто отражаться от тела. Отражение тепловых лучей подобно тому, как если бы световой луч отражался от зеркала. Поглощение теплового излучения подобно тому, как черная крыша сильно нагревается от солнечных лучей. А проникновение или прохождение лучей подобно тому, как лучи проходят в сквозь стекло или воздух. Наиболее распространенным в природе видом электромагнитного излучения является тепловое излучение.

Дата добавления: 2015-05-26