
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вопрос 34конвективный теплообмен
|
|
|
|
Рекомендуемые схемы обвязки теплообменников
Существует довольно много разнообразных схем качественного регулирования тепло- и холодопроизводительности ВНВ и ВОВ.
В каждом конкретном случае выбор схемы определяется заданным проектом, желаемым уровнем автоматизации процесса управления работой и защиты установки, финансовыми возможностями.
На (рис.1,2 и 3) показаны рекомендуемые схемы «обвязки» ВНВ.243 (рис.1,3) и ВОВ.243 (рис.2) с циркуляционными (смесительными) насосами и элементами системы автоматического регулирования (САУ).
Схема, изображенная на (рис.3), применяется, как правило, в тех случаях, когда гидравлические режимы тепловой сети стабильны, схемы, изображённые на (рис.1,2), могут использоваться и при наличии гидравлической нестабильности.
Во всех схемах в циркуляционном кольце происходит смешивание горячей или холодной воды, поступающей из сети с отработанной водой, поступающей из теплообменника.
Совмещение САУ с предложенными схемами определяет работу теплообменников в наиболее выгодном по температуре и гидравлическому давлению режиме.
Наиболее часто встречающейся причиной выхода из строя водяных воздухонагревателей в процессе эксплуатации является его замораживание, т.е. нарушение герметичности циркуляционного контура вследствие замерзания в нём воды.
Для избежания этого процесса рекомендуется использование САУ, элементы которой изображены на рисунках (1-3).
В комплект САУ входят: пульт управления, датчики (термостаты, термометры, манометры), исполнительные механизмы (электроприводы, клапаны, насосы).
Для защиты водяного воздухонагревателя от замораживания в процессе эксплуатации САУ предусматривает автоматический переход в режим аварийной работы теплообменника.
Аварийный режим вводится при понижении температуры воздуха на выходе из теплообменника до 10°С или температуры обратной воды до 30°С после срабатывания термостатов защиты по воде и по воздуху (см.рис.1-3).
При этом происходят следующие переходы:
— клапан воздухоприемного блока закрывается, прекращается проток воздуха через теплообменник;
— полностью открывается регулирующий воду клапан;
— циркуляционный насос работает;
— загорается индикаторная лампа, сигнализирующая об угрозе замораживания.
10.1.Основные понятия и определения
Передача теплоты конвекцией осуществляется перемещением в пространстве неравномерно нагретых объемов жидкости или газов. В дальнейшем изложении обе среды объединены одним наименованием — жидкость. Обычно при инженерных расчетах определяется конвективный теплообмен между жидкостью и твердой стенкой, называемый теплоотдачей. Согласно закону Ньютона—Рихмана, тепловой поток Q от стенки к жидкости пропорционален поверхности теплообмена и разности температур между температурой твердой стенки tc и температурой жидкости tж:
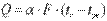 . .
| (10.1) |
Главная трудность расчета заключается в определении коэффициента теплоотдачи α, зависящего от ряда факторов: физических свойств омывающей поверхность жидкости (плотности, вязкости, теплоемкости, теплопроводности), формы и размеров поверхности, природы возникновения движения среды, скорости движения.
По природе возникновения различают два вида движения — свободное и вынужденное. Свободное движение происходит вследствие разности плотностей нагретых и холодных частиц жидкости, находящейся в поле действия сил тяжести; оно называется также естественной конвекцией и зависит от рода жидкости, разности температур, объема пространства, в котором протекает процесс.
Вынужденное движение возникает под действием посторонних побудителей (насоса, вентилятора, ветра). В общем случае наряду с вынужденным движением одновременно может развиваться и свободное. Относительное влияние последнего тем больше, чем больше разность температур в отдельных точках жидкости и чем меньше скорость вынужденного движения.
Движение жидкости может быть ламинарным или турбулентным. При ламинарном режиме частицы жидкости движутся послойно, не перемешиваясь. Турбулентный режим характеризуется непрерывным перемешиванием всех слоев жидкости. Переход ламинарного режима в турбулентный определяется значением безразмерного комплекса, называемого числом Рейнольдса:
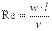 , ,
|
где w – скорость движения жидкости; ν — коэффициент кинематической вязкости1; l — характерный размер канала или обтекаемой стенки.
При любом режиме движения частицы жидкости, непосредственно прилегающие к твердой поверхности, как бы прилипают к ней. В результате вблизи обтекаемой поверхности вследствие действия сил вязкости образуется тонкий слой заторможенной жидкости, в пределах которого скорость изменяется от нуля на поверхности тела до скорости невозмущенного потока (вдали от тела). Этот слой заторможенной жидкости получил название гидродинамического пограничного слоя. Толщина этого слоя возрастает вдоль по потоку, так как по мере движения влияние вязкости распространяется все больше на невозмущенный поток. Однако и в случае турбулентного пограничного слоя непосредственно у стенки имеется очень тонкий слой жидкости, движение в котором носит ламинарный характер. Этот слой называется вязким, или ламинарным, подслоем.
Аналогично понятию гидродинамического слоя существует понятие теплового пограничного слоя — прилегающей к твердой поверхности области, в которой температура жидкости изменяется от температуры стенок tс до температуры жидкости вдали от тела tж. В общем случае толщины гидродинамического и теплового пограничных слоев пропорциональны, а для газов практически равны.
Интенсивность переноса теплоты зависит от режима движения жидкости в пограничном слое. При турбулентном пограничном слое перенос теплоты в направлении стенки обусловлен турбулентным перемешиванием жидкости. Однако непосредственно у стенки, в ламинарном подслое теплота будет переноситься теплопроводностью. При ламинарном пограничном слое теплота в направлении стенки переносится только теплопроводностью.
10.2.Дифференциальные уравнения конвективного теплообмена
На основании рассмотренного выше представления о процессах переноса теплоты при движении жидкости вдоль твердой поверхности получим уравнение, описывающее процесс теплоотдачи на границах тела. Так как у поверхности твердого тела имеется слой неподвижной жидкости, то для этого слоя можно использовать закон Фурье. Принимая, что ось Оу направлена перпендикулярно поверхности, запишем
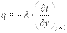 . .
|
Однако
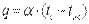 . .
|
Приравнивая эти уравнения получим
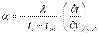 . .
| (10.2) |
Уравнение (10.2) называют дифференциальным уравнением теплоотдачи.
Если в дифференциальное уравнение теплопроводности подставить конвективное изменение температуры, обусловленное течением жидкости:
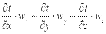 . .
|
где wx, wy и wz – проекции скорости жидкости на координатные оси, то можно записать
. 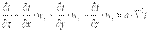
| (10.3) |
Иными словами говоря, если через изучаемый нами элементарный объём движется со скоростью w некое температурное поле, то дифференциальное уравнение теплопроводности следует накладывать на это поле.
Для строго описания процессов конвективного теплообмена к дифференциальному уравнению (10.3) следует добавить уравнение (Навье-Стокса) движения вязкой жидкости, вытекающее из второго закона Ньютона, уравнение сплошности и неразрывности жидкости и учесть зависимость плотности жидкости от температуры. Такая система уравнений описывает большой класс явлений — процессы конвективного теплообмена между жидкостью и твердой стенкой. Эти уравнения должны быть дополнены условиями однозначности, характеризующими конкретные особенности той или иной рассматриваемой задачи.
Конвективный теплообмен (КТ)– сложное явление распространения или передачи теплоты совместно конвекцией и теплопроводностью. Важнейшим видом КТ является теплоотдача.
Теплоотдача – обмен тепловой энергией между твердой поверхностью и подвижным теплоносителем.
В общем случае коэффициент теплоотдачи переменен по поверхности F. Он зависит от большого количества факторов и является функцией формы и размеров тела, режима движения, скорости и температуры жидкости, физических параметров жидкости и других величин. По-разному протекает процесс теплоотдачи в зависимости от природы возникновения движения жидкости.
Чтобы привести жидкость в движение, к ней необходимо приложить силу. Силы, действующие на жидкость, можно разделить на массовые (или объемные) и поверхностные. Массовыми называют силы, приложенные ко всем частицам жидкости и обусловленные внешними силовыми полями (например, сила тяжести). Поверхностные силы возникают вследствие действия окружающей жидкости или твердых тел; они приложены к поверхности контрольного объема жидкости. Такими силами являются силы внешнего давления и силы трения.
Основное уравнение теплоотдачи получено экспериментально и определяет количество теплоты, передаваемое поверхностью площадью F за время 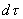 подвижному теплоносителю при заданной разности температур между теплоносителем и поверхностью.
подвижному теплоносителю при заданной разности температур между теплоносителем и поверхностью.
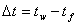
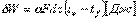
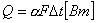
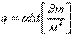
Закон Ньютона-Рифмана.
Целью исследования КТ является определение тепловых потоков. В соответствии с уравнением теплоотдачи для этого нужно знать значение коэффициента теплоотдачи 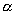 .
.
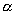 - величина расчетная. Для каждой области, для каждой конкретной задачи имеет свое значение. Коэффициент теплоотдачи
- величина расчетная. Для каждой области, для каждой конкретной задачи имеет свое значение. Коэффициент теплоотдачи 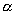 зависит от конфигурации тела или поверхности, от ее состояния, от температуры и разности температур, от физических свойств теплоносителя, от направления теплового потока
зависит от конфигурации тела или поверхности, от ее состояния, от температуры и разности температур, от физических свойств теплоносителя, от направления теплового потока
 .
.
Естественная (свободная) конвекция возникает под действием неоднородного поля внешних массовых сил (сил гравитационного, инерционного, магнитного, или электрического поля), приложенных к частицам жидкости внутри системы.
Вынужденная конвекция возникает под действием внешних поверхностных сил, приложенных на границах системы, или под действием однородного поля массовых сил, действующих в жидкости внутри системы. Вынужденная конвекция может осуществляться также за счет запаса кинетической энергии, полученной жидкостью вне рассматриваемой системы.
Задачи конвективного теплообмена описываются системой из 6 дифференциальных уравнений второго порядка, характеризующих перенос вещества и энергии в подвижных телах (системах). Для решения целого круга задач о тепловых потерях через ограждения, достаточно заменить сложную модель теплообмена в теплоносителе эквивалентной тепловой нагрузкой на границе теплоотдачи, и тогда достаточно рассчитать температурное поле внутри этого ограждения (т.е. твердого тела).
Вопрос 35
Закон Нью́тона — Ри́хмана — эмпирическая закономерность, выражающая тепловой поток между разными телами через температурный напор.
Теплоотдача — это процесс теплообмена между теплоносителем и твёрдым телом.
Теплопередача — это процесс передачи тепла от одной среды к другой через разделяющую их стенку. Закон утверждает, что
Плотность теплового потока (выражается в Вт/м²) на границе тел пропорциональна их разности температур (так называемый температурный напор):
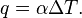
|
Коэффициент теплоотдачи[править | править исходный текст]
Коэффициент пропорциональности 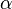 — коэффициент теплоотдачи (англ.) - плотность теплового потока при перепаде температур на 1K, измеряется вВт/(м²·К). В реальности он не всегда постоянен и может даже зависеть от разности температур, делая закон приблизительным. Если рассматривать тепловой поток как вектор, то он направлен перпендикулярно площадке поверхности, через которую протекает.
— коэффициент теплоотдачи (англ.) - плотность теплового потока при перепаде температур на 1K, измеряется вВт/(м²·К). В реальности он не всегда постоянен и может даже зависеть от разности температур, делая закон приблизительным. Если рассматривать тепловой поток как вектор, то он направлен перпендикулярно площадке поверхности, через которую протекает.
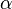 — количество теплоты, отдаваемое с 1 м² поверхности за единицу времени при единичном температурном напоре. Он зависит:
— количество теплоты, отдаваемое с 1 м² поверхности за единицу времени при единичном температурном напоре. Он зависит:
· от вида теплоносителя и его температуры;
· от температуры напора, вида конвекции и режима течения;
· от состояния поверхности и направления обтекания;
· от геометрии тела.
Поэтому 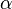 — функция процесса теплоотдачи; величина расчётная, а не табличная; определяется экспериментально.
— функция процесса теплоотдачи; величина расчётная, а не табличная; определяется экспериментально.
Эквивалентная запись:

Из вышеприведённой дифференциальной формулировки можно вывести интегральную:
Количество теплоты, отданное через площадку на границе раздела тел площадью 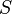 за время за время 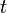 , пропорционально разности температур этих тел (если считать, что она остаётся за это время постоянной): , пропорционально разности температур этих тел (если считать, что она остаётся за это время постоянной):

|
Закон Ньютона служит одним из видов граничных условий (синоним — «условия третьего рода»), которые ставятся в задачах теплопроводности. В этом случае он записывается так (учтён также закон Фурье):
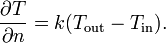
Заметим, что данный закон описывает ситуацию только на границе тела, внутри же температура определяется температуропроводностью тела. Тепловой поток внутри тела определяется по закону Фурье, что позволяет найти распределение, решив уравнение теплопроводности.
Если внутренняя теплопроводность намного больше, чем коэффициент теплоотдачи (иначе: маленькое число Био), то внутри устанавливается почти однородная температура (если на всей поверхности также она одинакова) и тогда можно записать уравнение охлаждения тела в виде:
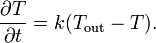
Здесь коэффициент 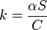 , где
, где 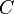 — теплоёмкость тела.
— теплоёмкость тела.
Из этого уравнения несложно получить, что температура тела в такой ситуации будет приближаться по экспоненте к температуре окружающей среды  :
:
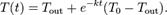
Вопрос 36
Уравнение теплопроводности — важное уравнение в частных производных, которое описывает распространение тепла в заданной области пространства во времени. Для решения задач, связанных с нахождением температурного поля, необходимо составить дифференциальное уравнение теплопроводности. Под дифференциальным уравнением обычно понимают математическую зависимость, выражаемую дифференциальным уравнением между физическими величинами, характеризующими изучаемое явление, причем эти физические величины являются функциями пространства и времени. Такое уравнение описывает протекание физического явления в любой точке тела в любой момент времени.
Дифференциальное уравнение теплопроводности устанавливает зависимость между температурой, временем и координатами элементарного объема.
|
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 1076; Нарушение авторских прав?; Мы поможем в написании вашей работы!