Граничные условия

Граничное условие может быть задано различными способами.

1. Граничное условие первого рода состоит в задании распределения температуры по поверхности тела в любой момент времени, т. е.

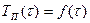(2.3)

где - температура на поверхности тела.

В частном случае , т. е. температура на поверхности постоянна на протяжении всего процесса теплообмена. Это может быть осуществлено при искусственном поддержании постоянной температуры или при особых условиях теплообмена между окружающей средой и поверхностью тела.

2. Граничное условие второго рода состоит в задании плотности теплового потока для каждой точки поверхности тела как функции времени, т. е.

(2.4)

Простейший случай граничного условия второго рода состоит в постоянстве плотности теплового потока:

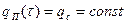(2.5)

Такой случай теплообмена имеет место при нагревании тел в высокотемпературных печах, где передача тепла в основном происходит при помощи излучения по закону Стефана – Больцмана, когда температура тела значительно меньше температуры излучающих поверхностей.

3. Граничное условие третьего рода характеризует закон конвективного теплообмена между поверхностью тела и окружающей средой при постоянном потоке тепла (стационарное температурное поле).В этом случае количества тепла, передаваемого в единицу времени с единицы площади поверхности тела в окружающую среду с температурой в процессе охлаждения (), прямо пропорционально разности температур между поверхностью тела и окружающей средой, т. е.

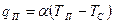(2.6)

где - коэффициент пропорциональности, называемый коэффициентом теплообмена (). Для процесса нагревания тела можно написать аналогичное соотношение, поменяв местами Т _п и Т_с. Коэффициент теплообмена числено равен количеству тепла, отдаваемого (или получаемого) единицей площади поверхности тела в единицу времени при разности температур между поверхностью и окружающей средой в 1⁰. Соотношение (2.6) можно получить из закона теплопроводности Фурье, полагая, что при обтекании поверхности тела жидкостью или газом передача тепла от жидкости к телу вблизи его поверхности происходит по закону Фурье:

(2.7)

где - коэффициент теплопроводности жидкости, - условная толщина пограничного слоя, .

4. Граничное условие четвертого рода соответствует теплообмену поверхности тела с окружающей средой (конвективный теплообмен тела с жидкостью) или теплообмену соприкасающихся твердых тел, когда температура соприкасающихся поверхностей одинакова.При обтекании твердого тела потоком жидкости (или газа) передача тепла от жидкости (газа) к поверхности тела в непосредственной близости к поверхности тела (ламинарный пограничный слой) происходит по закону теплопроводности (молекулярный перенос тепла), т. е. имеет место теплообмен, соответствующий граничному условию третьего рода

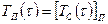(2.16)

Помимо равенства температур, имеет место также равенство потоков тепла

(2.17)Таким образом, при конвективном теплообмене твердого тела с жидкостью в случае стационарного температурного поля пользуются граничным условием третьего рода – соотношением (2.14), а в случае нестационарного температурного поля () необходимо при точной формулировке задачи применять граничные условия четвертого рода [соотношение (2.16), (2.17)]. В случае нестационарного лучистого теплообмена необходимо применять граничные условия второго рода (соотношение (2.4)). При малых разницах температур, когда , можно использовать граничное условие третьего рода. При этом величина будет обозначать коэффициент лучистого теплообмена .

Вопрос 37 Под конвективным теплообменом понимают процесс распространения тепла в жидкости (газе) от поверхности твердого тела или к его поверхности. Такой случай распространения тепла называют также теплоотдачей соприкосновением или просто теплоотдачей. При теплоотдаче тепло распространяется от поверхности твердого тела к жидкости (газу) через массу (ядро) жидкости (газа) преимущественно конвекцией. Конвекцией называют процесс переноса тепла вследствие движения и перемешивания макроскопических объемов газа или жидкости.

Основным законом теплоотдачи является закон Ньютона. Он формулируется следующим образом: количество тепла dQ, переданное от теплообменной поверхности к окружающей среде или, наоборот, от окружающей среды к теплообменной поверхности, прямо пропорционально поверхности теплообмена dF, разности температур теплообменной поверхности и окружающей среды и времени теплообмена τ. Аналитический вид закона Ньютона следующий:

dQ = αdF(tп - tс)dτ (2.1)

или для непрерывных процессов

Q = αF(tп - tс)

или

Q = (tп - tс)/(1/αF) =(tп - tс)/Rα

где 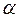- коэффициент теплоотдачи; tп - температура теплообменной поверхности; tс - температура окружающей среды, F - площадь поверхности теплоотдачи.

Величина 1/αF = R α называется термическим сопротивлением теплоотдачи.

Если количество теплоты определять за единицу времени и отнести его к единице поверхности теплоотдачи, то такую величину называют удельным тепловым потоком (тепловым напряжением, тепловым нагрузкой), или другими словами, тепловым потоком, и обозначают символом q; в этом случае формула Ньютона для теплового потока записывается в виде q= Q/F = α(tп - t с) (2.2)

Коэффициент теплоотдачи α, входящий в выражения (2.1) и (2.2), представляет собой количество тепла, передаваемого от единицы теплообменной поверхности в окружающую среду или, наоборот, от окружающей среды к единице теплообменной поверхности в течение единицы времени при разности температур теплообменной поверхности и окружающей среды, равной 1 К. Коэффициент теплоотдачи измеряется в ккал/(м2*ч*К).

Дифференциальное уравнение конвективного теплообмена (уравнение Фурье-Кирхгофа)

Конвективный перенос теплоты в движущихся потоках жидкости или газа описывается дифференциальным уравнением Фурье-Кирхгофа, решение которого должно позволить найти температуру в любой точке рабочего пространства в заданный момент времени. В наиболее общей форме уравнение Фурье-Кирхгофа для изотропной среды имеет вид

∂t/∂τ =а 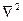t -[(wx(∂t/∂х)+ wy(∂t/∂y)+w z (∂t/∂z)]+qv/ρcp (2.3)

где cp - теплоемкость; ρ - плотность; 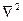- оператор Лапласа; qv –удельный источник теплоты, отнесенный к единице объема; w -скорость движения жидкости или газа; х, у, z - декартовы координаты.

Поскольку в уравнение (2.3) входит скорость движения жидкости или газа, интенсивность конвективного переноса теплоты зависит от распределения скоростей в потоке жидкости (газа), т.е от гидродинамической обстановки. Последняя зависит от режима движения жидкости (газа). Режим движения бывает свободным или вынужденным (принудительным).

Свободное движение жидкости (газа) или естественная конвекция, возникает вследствие разности плотностей нагретых и холодных частиц жидкости (газа) и определяется физическими свойствами жидкости (газа), её объемом и разностями температур нагретых и холодных частиц.

Вынужденное или принудительное движение жидкости (газа) возникает под действием какого-либо возбудителя (насоса, вентилятора, природного ветра) и определяется физическими свойствами жидкости (газа), её скоростью, формой и размерами канала, в котором осуществляется движение.

При вынужденном движении теплоносителя (жидкости, газа) различают ламинарный и турбулентный режим его движения. При ламинарном режиме движения создается достаточно большой пограничный слой, обтекающий воспринимающую теплоту поверхность материала и резко тормозящий теплопередачу. В турбулентном режиме движения пограничный слой очень тонок, теплоноситель носит неупорядоченный характер движения, и теплоотдача с поверхности материала конвективным путем резко возрастает.

Дата добавления: 2015-05-26