Введение. В данной курсовой работе мы рассматриваем синтез цифрового автомата

В данной курсовой работе мы рассматриваем синтез цифрового автомата. Теоретически мы по начально-заданной таблице входов и выходов разрабатываем модель логической схемы, по которой делаем электрическую схему, которую, реализовав на практике, получаем на реальном цифровом автомате.

В курсовой работе для решения поставленной задачи мы выполним ряд действий, к которым относят минимизация, декомпозиция, кодирование, определение функций выхода и возбуждения триггеров, упрощение логический функций и реализация этой логической функции на логических элементах.

Цель курсовой работы: изучить теоретическую основу разработки цифрового автомата и научится работать в ней.

Пояснительная записка

Глава I. Синтез абстрактного автомата.

1.1 Исходные данные.

Дана исходная таблица переходов и выходов:

X1	--/y2	5/--	1/y2	3/y2	10/--	3/--	4/у2	--/y2	1/--	3/y2
X2	3/y1	3/y1	6/--	3/y1	--/y1	--/y1	6/y1	9/y1	6/y1	8/у2
X3	7/--	7/у2	5/y1	2/y2	--/y2	7/y2	--/y2	6/у1	5/у2	2/y2
X4	10/y2	10/y2	4/y2	6/y2	4/y1	10/y2	4/y2	1/y2	4/--	--/--
X5	8/y2	8/y2	2/--	9/у1	2/у2	8/--	2/--	4/--	2/y2	3/y2

Разобьем исходную таблицу на таблицу переходов и таблицу выходов.

Таблица переходов:

X1	--						--
X2					--	--
X3					--		--
X4										--
X5

Таблица выходов:

X1	Y2	--	Y2	--	--	Y2	Y2	Y1	--	Y1
X2	Y1	Y1	--	Y1	Y1	Y1	Y1	Y1	Y1	Y2
X3	--	Y2	Y2	Y2	Y2	Y2	Y2	Y1	Y2	Y2
X4	Y2	Y2	Y2	Y2	Y1	Y2	Y2	Y2	--	--
X5	Y2	Y2	--	Y1	Y2	--	--	--	Y2	Y2

1.2 Минимизация поалгоритму Ангера – Пола

Для минимизации цифрового автомата осуществляется последовательное попарное сравнение состояний и оценка степени их совместимости.

По степени совместимости состояния бывают:

· Абсолютно несовместимые – состояния имеющие разные выходные сигналы.

· Абсолютно совместимые – состояния, имеющие одинаковые выходные сигналы и равные функции перехода.

· Условно совместимые – состояния, совместимые при условии равенства функций выхода и эквивалентности функций перехода.

1.2.1 Составление треугольной матрицы

Для нахождения минимального частично-определенного автомата необходимо составить треугольную матрицу Ангера-Полла.

Треугольная матрица заполняется в 3 этапа:

1 этап:

На первом этапе мы определяем абсолютно несовместимые состояния, попарно сравнивая столбцы в таблице выходов.

Если значение 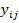не равно значению 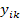, то ставим «X» в соответствующей ячейке.

2 этап:

На втором этапе мы определяем абсолютно-совместимые состояния, попарно сравнивая столбцы в таблице переходов, пропуская те пары, что мы определили как абсолютно несовместимые. Если состояния одинаковы при одинаковых сигналах, то ставим «V» в соответствующей ячейке.

3 этап:

На третьем этапе мы определяем условно-совместимые состояния, производя попарное сравнение состояний, по таблице переходов, и в соответствующую ячейку матрицы Ангера-Пола записываем условие, при котором рассматриваемые состояния совместимы.

После выполнения описанных действий мы получим матрицу Ангера-Пола:

	V
	3-6, 2-8, 5-7, 4-10	5-1, 8-2, 3-6, 2-5
	X	X	1-10, 6-4, 6-3, 2-3, 5-2
	10-4, 8-2	X	X	X
	V	V	1-5, 2-8, 5-7, 4-10	X	3-5, 4-10, 2-8
	3-6, 4-10, 8-2	3-6, 4-10, 2-8	V	X	4-4, 2-2	10-4, 8-2
	3-9, 4-8, 6-7, 10-1	X	X	X	X	X	X
	3-6, 9-2, 9-7, 4-10	1-5, 4-10, 6-3, 8-2, 5-7	V	X	1-3, 4-4, 2-2	5-1, 8-2, 10-4	X	3-6, 4-2, 6-5, 1-4
	X	X	X	X	X	X	X	X	1-3, 2-5, 6-8, 5-2

1.2.2 Определение совместимых состояний

Для нахождения несовместимых (а так же совместимых) пар состояний треугольная таблица просматривается по столбцам, начиная с нижнего правого (т.е. 9-10). С правого нижнего столбца мы ищем первую ячейку, отмеченную крестом. В нашем случае это (8,10).Тогда во всех клетках, где есть пара (8,10), ставится крест. Эту процедуру мы проводим для всех клеток, отмеченных крестом (в том числе и свежеотмеченные), и заканчиваем, когда таких клеток не остаётся. В этом случае клетки без крестов соответствуют совместимым парам состояний, а клетки с крестами – несовместимым.

В итоге получаем окончательный вариант матрицы Ангера-Пола:

	V
	X	X
	X	X	X
	X	X	X	X
	V	V	X	X	X
	X	X	V	X	X	X
	X	X	X	X	X	X	X
	X	X	V	X	X	X	V	X
	X	X	X	X	X	X	X	X	X

После выполнения этих действий мы получаем совместимые пары состояний – 1-2, 1-6, 2-6, 3-7, 3-9, 7-9.

1.2.3 Минимизированный цифровой автомат

Для получения минимизированного автомата мы рассматриваем совокупность максимальных множеств. Составление максимальных классов совместимости осуществляется по матрице Ангера-Пола. Все состояния, на пересечениях которых присутствует «V», считаются совместимыми. Рассмотрение максимальных классов совместимости осуществляются с крайнего правого столбца, имеющего, по крайней мере, одну клетку без «Х».

1. (S₇;S₉) Ф=(7,9)

2. (S₃;S₉)&(S₃;S₇)&(S₇;S₉) Ф=(3,7,9)

3. (S₂;S₆) Ф=(2,6)

4. (S₁;S₆)&(S₁;S₇)&(S₆;S₂) Ф=(1,6,2)

Таким образом, получаем следующие максимальные множества:

b₁={1,2,6}, b₂={4}, b₃={5},b₄={3,7,9}, b₅={8}, b₆={10}.

Из этого получаем, что в минимизированном автомате будет 6 состояний, 5 входных сигналов и 2 выходных сигнала.

Построим таблицы переходов и выходов минимизированного автомата.

Заполнение таблицы переходов минимизированного автомата мы будем осуществлять путем сравнения с исходной таблицей переходов.

Например: в b1 входят состояния {1,2,6}. При входном сигнале x1 они все перейдут в состояние {5}, входящее в b3. Значит на пересечении {b1,x1} таблицы переходов минимизированного автомата мы запишем b3. Таким способом заполняем все ячейки.

Таблица переходов минимизированного автомата:

δ	b1	b2	b3	b4	b5	b6
x1	b3	b6	b4	b1	b3	b4
x2	b4	b4	b1	b1	b4	b5
x3	b4	b1	b1	b3	b1	B1
x4	b6	b1	b2	b2	b1	b1
x5	b5	b4	b1	b1	b2	b4

Алгоритм заполнения таблицы выходов минимизированного автомата аналогичен заполнению таблицы переходов минимизированного автомата, только в данном случае мы сравниваем с исходной таблицей выходов.

Таблица выходов минимизированного автомата:

λ	b1	b2	b3	b4	b5	b6
x1	y2	y1	y1	y2	y1	y1
x2	y1	y1	y1	y1	y1	y2
x3	y2	y2	y2	y2	y1	y2
x4	y2	y2	y1	y2	y2	y1
x5	y2	y2	y2	y2	y1	y2

1.3 Декомпозиция автоматов

Задача декомпозиции состоит в получении сети автоматов реализующих функции заданного автомата. Декомпозиция основана на разбиении множеств состояний автоматов.

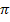-разбиением множества S является множество его подмножеств которые не пересекаются между собой и при объединении дают множество S. Эти подмножества называются блоками -разбиения.

Разбиение 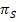называется СП-разбиением, при условии что если состояния находятся в одном блоке, то при одинаковом входном взаимодействии состояния в которые перейдет автомат будут также находиться в одном блоке.

1.3.1 Определение СП разбиений

Определение СП-разбиений основано на предположении, что рассматриваемые состояния находятся в одном блоке. Если в разных блоках совпадает хотя бы 1 состояние, то эти блоки объединяются.

Ищем СП-разбиения, попарно рассматривая все состояния:

{1 2} X1{36} объединяем блоки, имеющие хотя бы одно одинаковое состояние и

X2 {4} получаем один блок {123456}. Это значит, что в данном случае

X3{41} => СП-разбиения нет. В таком случае ставил «Х»

X4{61} Аналогично рассматриваем все пары состояний

X5{54}

{13} X1{34} {1345}X1{134}

X2{4} X2{14}

X3{4} => {1345}{62}; X3{134} => {123456}; X

X4{62} X4{126}

X5{54} X5{125}

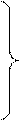{14} X1{13} {1245} X1{134}

X2{14} X2{14}

X3{34} => {1345}{26}; X3{134} => {123456}; X

X4{26} X4{126}

X5{15} X5{125}

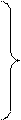
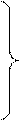{15} X1{3} {12456} X1{1346}

X2{4} X2145}

X3{14} => {12456}{3}; X3{134} => {123456}; X

X4{16} X4{126}

X5{25} X5{1245}

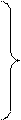
{16} X1{34} {13456} X1{134}

X2{45} X2{145}

X3{14} => {13456}{3}; X3{134} => {123456}; X

X4{6} X4{126}

X5{45} X5{1245}

{23} X1{46} {12346} X1{1346}

X2{4} X2{145}

X3{1} => {12346}{5}; X3{143} => {123456}; X

X4{12} X4{126}

X5{14} X5{1245}

{24} X1{16} {12346} X1{1345}

X2{14} X2{145}

X3{13} => {12346}{5}; X3{143} => {123456}; X

X4{12} X4{126}

X5{13} X5{1245}

{25} X1{34} {245} X1{136}

X2{4} X2{14}

X3{1} => {1}{245}{36}; X3{13} => {123456}; X

X4{1} X4{12}

X5{24} X5{124}

{26} X1{46} {2456} X1{1345}

X2{45} X2{145}

X3{1} => {1}{2456}{3}; X3{13} => {123456}; X

X4{1} X4{12}

X5{4} X5{124}

{34} X1{14} {134} X1{134}

X2{1} X2{14}

X3{3} => {134}{2}{5}; X3{34} => {1345}{26};

X4{2} X4{26}

X5{1} X5{15}

{1345} X1{134}

X2{14}

X3{3134} => {123456}; X

X4{126}

X5{125}

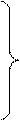
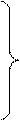{35} X1{34} {12} X1{36}

X2{4} X2{4}

X3{1} => {12}{345}; X3{41} => {123456}; X

X4{12} X4{61}

X5{12} X5{54}

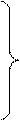{33} X1{4}

X2{5}

X3{1} => {14}{36}{2};

X4{2}

X5{14}

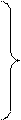
{14} X1{13} {1245} X1{134}

X2{14} X2{14}

X3{34} => {1345}{26}; X3{134} => {123456}; X

X4{26} X4{126}

X5{15} X5{125}

{45} X1{13}

X2{14}

X3{13} => {123456};

X4{12}

X5{12}

{46} X1{14} {13456} X1{134}

X2{15} X2{145}

X3{13} => {13456}{2}; X3{134} => {123456}; X

X4{2} X4{126}

X5{14} X5{1245}

{56} X1{34} {23456} X1{1346}

X2{45} X2{145}

X3{1} => {1}{23456}; X3{13} => {123456}; X

X4{24} X4{12}

X5{24} X5{124}

Отсюда следует, что СП-разбиений нет.

1.3.2 Декомпозиция автоматов при отсутствии СП-разбиений

При отсутствии СП-разбиений декомпозируемые автоматы соединяются в сеть, следовательно, на входе и выходе автоматов будут существовать логические функции преобразования входных и выходных сигналов. Задача декомпозиции при отсутствии СП-разбиений сводится к определению ортогональных π-разбиений и реализацию на их основе автоматов.

Определим ортогональные π-разбиения из множества состояний минимизированного автомата.

π1={1234; 56}, π2={1256; 34}, π3={135; 246}.

Каждое π-разбиение соответствует новому автомату, т.е обозначим блоки π-разбиений через состояния автоматов:

π1->E{e1=1234; e2=56}

π2->C{c1=1256; c2=34}

π3->D{d1=135; d2=246}.

Для каждого разбиения построим функцию перехода компонентных автоматов на основе функции перехода исходного автомата. Функции переходов компонентных автоматов определяют реакцию автоматов E, C, D на внешнее входное воздействие и что исходный автомат находится в состояние К, соответствующему произведению алфавитов компонентных автоматов.

e₁*c₁*d₁=1 e₂*c₁*d₁=5

e₁*c₁*d₂=2 e₂*c₁*d₂=6

e₁*c₂*d₁=3 e₂*c₂*d₁= *

e₁*c₂*d₂=4 e₂*c₂*d₂= *

Дата добавления: 2015-05-26