
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Автомат D
|
|
|
|
Автомат C
Автомат E
| δ | ||||||
| x1 | e1 | e2 | e1 | e1 | e1 | e1 |
| x2 | e1 | e1 | e1 | e1 | e1 | e2 |
| x3 | e1 | e1 | e2 | e1 | e1 | e1 |
| x4 | e2 | e1 | e1 | e1 | e1 | e1 |
| x5 | e2 | e1 | e1 | e1 | e1 | e1 |
| δ | ||||||
| x1 | c2 | c1 | c2 | c1 | c2 | c2 |
| x2 | c2 | c2 | c1 | c1 | c2 | c1 |
| x3 | c2 | c1 | c1 | c2 | c1 | c1 |
| x4 | c1 | c1 | c1 | c1 | c1 | c1 |
| x5 | c1 | c2 | c1 | c1 | c1 | c2 |
| δ | ||||||
| x1 | d1 | d2 | d2 | d1 | d1 | d2 |
| x2 | d2 | d1 | d1 | d1 | d1 | d1 |
| x3 | d2 | d1 | d1 | d1 | d1 | d1 |
| x4 | d2 | d1 | d2 | d2 | d1 | d1 |
| x5 | d1 | d2 | d1 | d1 | d1 | d2 |
Для того, чтобы определить взаимное влияние автоматов друг не друга, определяют τ и Ө–разбиение для каждого автомата в отдельности.
τ –разбиения устанавливают равенства функции переходов для различных состояний автоматов при одинаковом входном воздействии.
Ө–разбиение устанавливает равенство функций переходов из одного и того же состояния, но при различных входных сигналах.
Определим τ–разбиения для компонентных автоматов, путем сравнения столбцов таблиц переходов:
τe= {123};{25};{6}.
τc ={1};{2};{3}; {4}; {5}; {6}.
τd = {1};{26};{3};{4};{5}.
Определим η–разбиения для компонентных автоматов, путем сравнения строк таблиц их переходов:
Өe = {12};{34};{56}.
Өc = {1};{2};{3};{4}: {5}.
Өd = {1};{23};{4};{5}.
1.3.3 Определение входных сигналов компонентных автоматов и составление таблиц
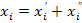 Влияние автоматов друг на друга определяется по следующему правилу: если произведение π-разбиений i-го автомата меньше или равно τ-разбиению i-го автомата, то составляющая
Влияние автоматов друг на друга определяется по следующему правилу: если произведение π-разбиений i-го автомата меньше или равно τ-разбиению i-го автомата, то составляющая  определяется как произведение π-разбиений исключая π-разбиение i-го автомата.
определяется как произведение π-разбиений исключая π-разбиение i-го автомата.
π1*π2={12,34,56}
π1*π3={13,5,24,6}
π2*π3={15,26,3,4}
π1*π2*π3={1,2,3,4,5,6}
При сравнении произведений π-разбиений и τ-разбиений автоматов видно, что автоматы непосредственно не влияют на входные сигналы друг друга. Однако, при рассмотрении ортогональных π-разбиений видно, что на входной сигнал автомата С влияют D и E совместно, на входной сигнал автомата D – С и E совместно, а на входной сигнал автомата E – C и D совместно. Следовательно, составляющая входного сигнала 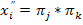 .
.
Для составления таблиц переходов автоматов C,D и E примем следующие обозначения:
E{e1=1234; e2=56}
C{c1=1256; c2=34}
D{d1=135; d2=246}
U={u1=x1,x2; u2=x3; u3=x4; u4=x5}
V={v1=x1; v2=x2,x3; v3=x4; v4=x5}
W={w1=x1; w2=x2,x3; w3=x4; w4=x5}.
Таблицы заполняем по следующему алгоритму на примере первой ячейки:
c1*d1*e1=1. По сигналу u1(x1,x2) автомат E перейдет в состояния e1, что мы и запишем в первую ячейку таблицы переходов автомата E.
Таким образом заполняются все ячейки всех трёх автоматов:
| δ | e1 | e2 | δ | c1 | c2 | δ | d1 | d2 | ||
| c1*d1, u1 | e1 | e1 | e1*d1, v1 | c2 | c2 | e1*c1, w1 | d1 | d2 | ||
| c1*d2, u1 | e2 | e1 | e1*d2, v1 | c1 | c1 | e1*c2, w1 | d2 | d1 | ||
| c2*d1, u1 | e1 | e1 | e2*d1, v1 | c2 | c1 | e2*c1, w1 | d1 | d2 | ||
| c2*d2, u1 | e1 | e1 | e2*d2, v1 | c2 | c1 | e2*c2, w1 | d1 | d1 | ||
| c1*d1, u2 | e1 | e1 | e1*d1, v2 | c2 | c1 | e1*c1, w2 | d2 | d1 | ||
| c1*d2, u2 | e1 | e2 | e1*d2, v2 | c2 | c1 | e1*c2, w2 | d1 | d1 | ||
| c2*d1, u2 | e1 | e1 | e2*d1, v2 | c2 | c1 | e2*c1, w2 | d1 | d1 | ||
| c2*d2, u2 | e1 | e1 | e2*d2, v2 | c1 | c1 | e2*c2, w2 | d1 | d1 | ||
| c1*d1, u3 | e1 | e1 | e1*d1, v3 | c2 | c1 | e1*c1, w3 | d2 | d1 | ||
| c1*d2, u3 | e1 | e1 | e1*d2, v3 | c1 | c2 | e1*c2, w3 | d2 | d2 | ||
| c2*d1, u3 | e2 | e1 | e2*d1, v3 | c1 | c1 | e2*c1, w3 | d1 | d1 | ||
| c2*d2, u3 | e1 | e1 | e2*d2, v3 | c1 | c1 | e2*c2, w3 | d1 | d1 | ||
| c1*d1, u4 | e2 | e1 | e1*d1, v4 | c1 | c1 | e1*c1, w4 | d1 | d2 | ||
| c1*d2, u4 | e1 | e1 | e1*d2, v4 | c1 | c1 | e1*c2, w4 | d1 | d1 | ||
| c2*d1, u4 | e1 | e1 | e2*d1, v4 | c1 | c1 | e2*c1, w4 | d1 | d2 | ||
| c2*d2, u4 | e1 | e1 | e2*d2, v4 | c1 | c1 | e2*c2, w4 | d1 | d1 | ||
| e1*d1, v5 | c1 | c1 | ||||||||
| e1*d2, v5 | c2 | c1 | ||||||||
| e2*d1, v5 | c1 | c1 | ||||||||
| e2*d2, v5 | c2 | c1 |
Определение выходных сигналов осуществляется по произведению состояний компонентных автоматов E, C и D и входным сигналам в соответствии с таблицей выходов автомата B.
| g | c1*d1*e1 | c1*d1*e2 | c1*d2*e2 | c2*d1*e1 | c2*d2*e2 |
| x1 | y2 | y1 | y1 | y2 | y1 |
| x2 | y1 | y1 | y1 | y1 | y1 |
| x3 | y2 | y2 | y2 | y2 | y1 |
| x4 | y2 | y2 | y1 | y2 | y2 |
| x5 | y2 | y2 | y2 | y2 | y1 |
Глава II. Структурный синтез цифрового автомата.
2.1 Кодирование автомата.
На основании таблиц переходов и логической функции строится структурная схема сети автоматов. Структурный автомат представляет собой композицию комбинационной (логической) схемы и элементов памяти, связанных со схемой. Входными переменными схемы являются входные переменные автомата - сигналы приходящие на блоки Ue, Vc, Wd. Выходы схемы Fe, Fc, Fd определяют переход автомата в следующее состояние.
Переход от абстрактного автомата к структурному осуществляется через c помощью кодирования входов, выходов и состояний абстрактного автомата.
Кодирование входных переменных состоит в сопоставлении каждому символу входного алфавита абстрактного автомата набора значений двоичных переменных <x1, x2, …,xn> таким образом, чтобы каждый символ алфавита имел уникальный, отличный от других символов, вектор. Для этого необходимо, чтобы выполнялось условие N£2n, где N – число символов входного алфавита.
Кодировать таблицы переходов и выходов будем в соответствии с условиями:
c1d1= e1c1= e1d1= 00 u1=w1= 00 v1= 000
c1d2= e1c2= e1d2= 01 u2=w2= 01 v2= 001
c2d1= e2c1= e2d1= 10 u3=w3= 10 v3= 010
c2d2= e2c2= e2d2= 11 u4=w4= 11 v4= 011
v5= 111
Получим закодированные таблицы переходов компонентных автоматов:
| δ | δ | c1 | c2 | δ | d1 | d2 | ||||
Теперь получим закодированную таблицу переходов выходных сигналов, для этого примем следующие обозначения:
x1= 000 b1= 000 y1= 1 y2=0
x2= 001 b2= 001
x3= 010 b3= 010
x4= 011 b4= 100
x5= 111 b5= 011
b6= 111
| g | ||||||
При синтезе цифровых автоматов применяются триггеры счета или триггеры типа «линия задержки»
Закодируем полученные нами таблицы переходов компонентных автоматов с помощью триггера счета. Для этого проведем инверсию столбцов «1»:
| δ | δ | c1 | c2 | δ | d1 | d2 | ||||
| * | * | |||||||||
| * | * | * | * | |||||||
| * | * | |||||||||
| * | * | * | * | |||||||
| * | * | |||||||||
| * | * | * | * | |||||||
| * | * | |||||||||
| * | * | * | * | |||||||
| * | ||||||||||
| * |
2.2 Определение функций логики
2.2.1 Определение функции выхода
Данная функция определяется из таблицы выходов:
| g | ||||||
Функция выхода определяется из кодированной таблицы выходов по следующей методике: если обозначить кодирующие переменные входа как а1, а2 и а3,
состояний – как t1, t2, t3, выхода – как g, то функция выхода будет иметь вид:

2.2.2 Определение функции возбуждения триггеров.
Опять обозначим кодирующие переменные входа как a1, a2 и a3, состояний – как t, заменив в матрице выходов состояния на их коды, получим описание функций u(t1), u(t2), u(t3).
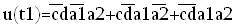

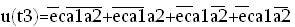
2.3 Упрощение логических функций.
Для упрощения функций u(t1), u(t2) и u(t3) используем карты Карно:
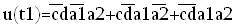
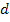
| 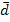
| ||||

| 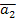
| ||||
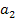
| |||||
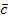
| |||||
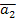
| |||||
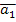
| 
| 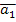
|
По карте видно, что упростить функцию мы не можем, значит, мы оставляем её без изменений.
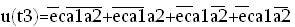

| 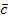
| ||||
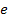
| 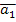
| ||||

| |||||

| |||||
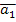
| |||||
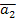
| 
| 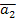
|
Получим упрощённую функцию u(t3):
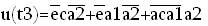
Для упрощения функций u(t2) и g воспользуемся склеиванием и поглощением, а так же импликантной таблицей.



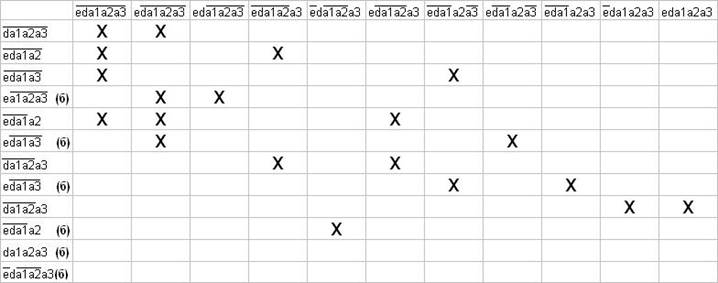
Как видно по импликантной таблице,
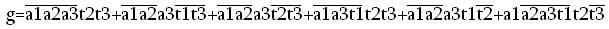

Глава III. Разработка комбинационных
логических схем.
Мы получили 4 логические функции, которые необходимо реализовать на практике:
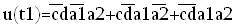

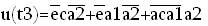
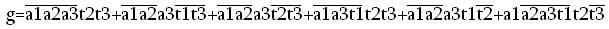
3.1 Логическая схема компонентного автомата E.
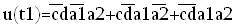
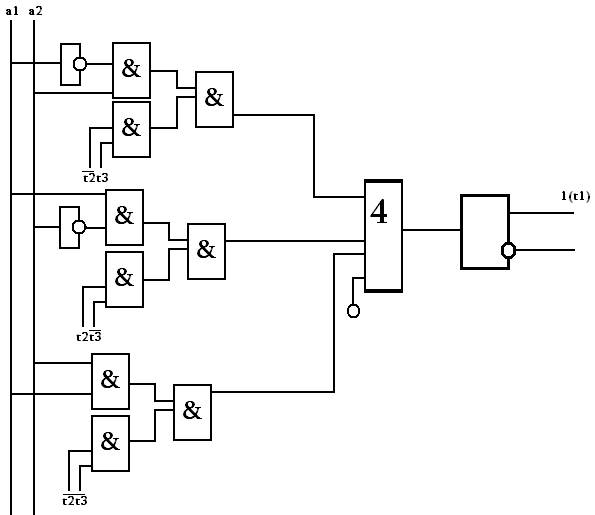
Для этой схемы мы используем 1 схему 4-ИЛИ, 9 схем И, и 2 схемы НЕ.
3.2 Логическая схема компонентного автомата С.


Для этой схемы мы используем 23 схемы И, 8 схем НЕ и 2 схемы 4-ИЛИ и схему 2-ИЛИ.
3.3 Логическая схема компонентного автомата D.

Здесь мы используем 3 схемы НЕ, 3 схемы И, схему ИЛИ.
3.4 Логическая схема выхода.

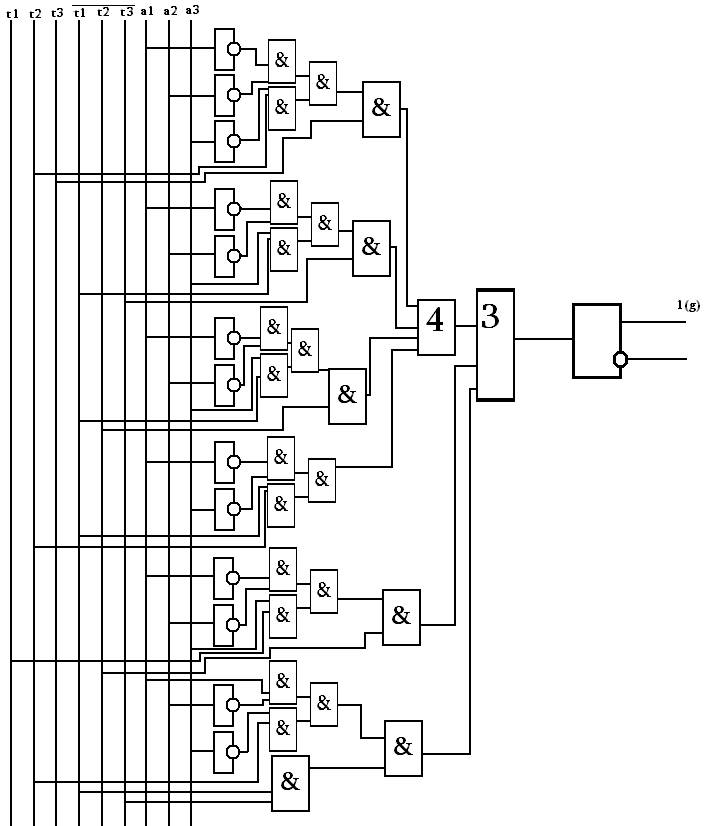
Здесь мы используем 11 схем НЕ, 24 схемы И, схемы 4-ИЛИ и 3- ИЛИ.
Заключение.
В данной курсовой работе мы рассмотрели синтез цифрового автомата. Теоретически мы по начально-заданной таблице входов и выходов разработали модель логической схемы, по которой сделали электрическую схему, реализовав на практике функцию V1, получили часть реального цифрового автомата.
В курсовой работе для решения поставленной задачи мы выполнили ряд действий, к которым относят минимизация, декомпозиция, кодирование, определение функций выхода и возбуждения триггеров, упрощение логический функций и реализация этой логической функции на логических элементах.
Мы изучили теоретическую основу разработки цифрового автомата и научились работать в ней.
|
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 631; Нарушение авторских прав?; Мы поможем в написании вашей работы!