З’єднуючи задану вершину А з отриманою граничною точкою проводять другу сторону кута А . Кут А є перспективою заданого кута 60°

Далі будують натуральну величину кута 60° при сполученій точці зору і заданій стороні. Для цього з'єднують граничну точку зі сполученою точкою зору. Відкладають натуральний кут 60° з вершиною і стороною. Потім продовжують другу сторону кута до перетинання з лінією обрію і визначають її граничну точку.

Мал. 70 Мал. 71

Для визначення натуральної величини кута, що лежить у горизонтальній площині, по його зображенню на картині будують граничні точки сторін кута, продовживши їх до перетинання з лінією обрію. Отримані граничні крапки з'єднують із сполученою точкою зору. Кут при сполученій точці зору буде натуральною величиною кута, заданого на картині.

§ 18. ПОБУДОВА ОКРУЖНОСТІ У ПЕРСПЕКТИВІ

Загальні поняття. Уміння будувати в перспективі окружність потрібно не тільки для зображення на картині круглих предметів, але і для показу різних положень між окремими елементами предметів, наприклад напіввідчиненого вікна або двері, нахиленої картини або дзеркала, обрису тіней від круглих предметів і ін.

У перспективі зображення окружності може мати різний обрис. Це залежить від того, як розташована площина окружності щодо картини і точки зору.

В окремому випадку перспективою окружності буде окружність, якщо вона розташована в площині, паралельній картині, і її геометричний центр збігається з точкою Р. Іншій окремий випадок перспективи окружності — прямолінійний відрізок. Таке зображення виходить тоді, коли всі промені зору, спрямовані до точок зображуваної окружності, розташовані в одній променевій площині (наприклад, окружність у площині обрію або у площині головного променя зору). У всіх інших положеннях окружність на картині зобразиться лекальною кривою.

Побудова перспективи окружності на апарат, що проектує, полягає у визначенні точок перетинання променів зору, які проведені до точок заданої окружності, з картинною площиною. Сукупність цих променів зору утворить поверхню променевого конусу. Звідси перспектива окружності являє собою лінію перетинання поверхні променевого конуса з площиною картини.

У практиці побудови перспективи окружності найбільш часто зустрічається еліпс. З геометрії відомо, що це замкнена плоска крива, яка симетрична відносно двох взаємно перпендикулярних вісей (мал. 72, а). Велике та мала вісі еліпса перетинаються у центрі та розподіляються навпіл. Помітимо, що еліпси – зображення окружності у перспективі – втрачають ці властивості (мал. 72, б).

Щоб побудувати зображення окружності у перспективі знаходять окремі точки, яки належать кривій, та плавно з’єднують їх від руки. Плавність обрису ліній досягається досить великим числом точок, які розташовані близько одна до одній.

Треба пам’ятати, що яким би вузьким не був еліпс, він не буде мати гострих кутів і малюватися з чітко баченими закругленнями (мал. 72, в).

а) б) в)

Мал. 72

Способи побудови зображень окружності в перспективі

Відомо кілька способів побудови окружності в перспективі. Основним, найбільш простим і зручним, є спосіб описаного квадрата. Сутність його полягає в тім, що спочатку будують у перспективі квадрат, потім у нього вписують окружність, визначивши вісім точок — середини сторін квадрата і перетинання окружності з його діагоналями. Цей спосіб зручно застосовувати при зображенні в перспективі окружності невеликих розмірів.

Виконаємо таку побудова окружності, що лежить у предметній площині. Для цього задають натуральну величину окружності, вписаної в квадрат і сполученої з площиною картини. Для спрощення побудови одну зі сторін квадрата сполучають з основою картини (мал. 73).

Побудову виконують у наступній послідовності. Спочатку будують перспективу квадрата і відзначають на ньому чотири точки, що лежать на серединах його сторін. В окружності ці точки будуть кінцями вертикального (1 — 3) і горизонтального (2 — 4) діаметрів. Для їхнього знаходження проводять глибинні прямі, що відповідають напрямкам вертикальних сторін квадрата і діаметра окружності. Через правий (чи лівий) кут квадрата проводять його діагональ із точкою сходу D₁ (чи D₂).

Перетинання діагоналі з лівою стороною квадрата визначить у перспективі його вершину і далеку сторону. Перетинання діагоналі з глибинною прямою — зображенням вертикального діаметра окружності — визначить її центр і горизонтальний діаметр. Кінці діаметрів окружності лежать на серединах сторін квадрата. У перспективі вони визначать чотири точки еліпса: 1, 2, 3, 4.

Мал. 73 Мал. 74 Потім будують ще чотири точки перетинання діагоналей квадрата з окружністю (5, 6, 7, 8). Для цього в сполученому фронтальному положенні квадрата проводять дві допоміжні прямі через точки 5 і 6, 7 і 8, паралельні вертикальному діаметру окружності. У перспективі вони будуть глибинними прямими, що у перетинанні з діагоналями квадрата визначать ще чотири точки еліпса: 5, 6, 7, 8. З'єднавши послідовно всі добудовані точки плавною лінією, одержують зображення окружності в перспективі — еліпс.

При використанні способу описаного квадрата можна спростити побудову. Для цього в сполученому положенні з картиною будують половину квадрата (мал. 74) або його чверть і вписують в них відповідно половину або чверть окружності.

Якщо відстань між деякими точками дуже велико, то застосовують проміжні, додаткові точки. Їх знаходять у перетинанні окружності з допоміжною прямою, що проходить через центр О. Так (див. мал. 74) на окружності знайдена точка 9 у перетині глибинної прямої з допоміжною, яка проведена через центр еліпса. У такий же спосіб побудована точка 10. Визначивши у перспективі точки 9 і 10, можна побудувати симетрично їм ще пару точок: 11 і 12, відклавши на горизонтальних прямих відповідну половину хорди.

При побудові в перспективі зображення великої окружності для забезпечення максимальної точності знаходять до 16 точок й більш. Для цього застосовують спосіб побудови парних точок, зв'язаних діагоналлю квадрата, описаного біля даної окружності.

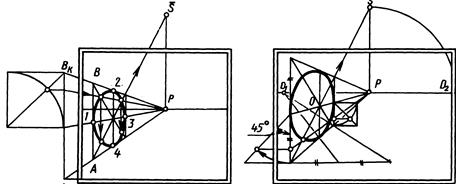
Задамо на картині (мал. 75) перспективу квадрата з центром О і відзначимо точки еліпса, що лежать на його сторонах і діагоналях. В даному прикладі для побудови використане не сполучене положення окружності з картиною, а фронтальна площина, побудована при далекій стороні квадрата. Помітимо, що тут побудована лише чверть окружності і її радіус відповідає половині сторони квадрата в перспективі. На фронтальній окружності відзначають точки 9 і 10, які симетричні щодо діагоналі. Потім через відзначені точки проводять горизонтальні і вертикальні лінії (тут вони штрихові), які будуть перетинати діагоналі квадрата.

Мал. 75 Мал. 76 Мал. 77

Далі цю ж побудову виконують у перспективі. Відповідно до положення вертикальних прямих будують глибинні прямі з точкою сходу Р. А через точки перетинання їх з діагоналями проводять горизонтальні прямі, що визначать у перспективі положення точок 9 і 10. На малюнку відзначені дві пари точок лівої половини квадрата. Симетрично їм праворуч можна побудувати, як у попередньому прикладі, ще дві пари точок, відклавши відрізки хорд.

Якщо окружність розташована у вертикальній площині, то застосовують той же спосіб описаного квадрата і виконують побудови, аналогічні попереднім прикладам. Так, спочатку на картині (мал. 76) у вертикальній площині будують перспективу квадрата з заданою стороною А_оВ­_к і визначають чотири точки еліпса, які лежать на його сторонах (1, 2, 3, 4). Потім знаходять точки перетинання діагоналей квадрата з окружністю, для чого використовують допоміжні прямі, що на картині є глибинними. Сполучений квадрат, у який вписана окружність (у даному прикладі узята його 1/4 частина), розташовують збоку при картинному сліді А_оВ_к площини. Для побудови точок, розташованих на діагоналях, застосовують фронтальне положення квадрата, заданого при ближній чи далекій його стороні. Помітимо, що можна будувати тільки 1/8 частину окружності, як це показано на малюнку 77.

§ 19. ПОБУДОВА В ПЕРСПЕКТИВІ ЗОБРАЖЕНЬ КРУГЛИХ ПРЕДМЕТІВ

Розглянуті в попередньому параграфі побудови дозволяють зображувати на картині досить точно предмети, що мають круглі обриси форм (стіл, ваза, арки мостів, циліндричні зводи перекриттів і ін.), а також предмети напіввідчинені і похилі (двері, вікно, кришка коробки, картина й ін.). Розглянемо приклади зображення предметів у перспективі з застосуванням побудови окружності, що лежить у по-різному розташованих площинах.

Площина окружності горизонтальна. На картині (мал. 78) показана побудова вертикального циліндра, у якого задані діаметр основи і висота. Для цього відзначають у предметній площині довільно центр окружності О, на основі картини — натуральну величину радіуса окружності, а на бічній стороні рамки картини — висоту циліндра.

Мал. 78

Спочатку задають сполучене положення чверті квадрата у відповідності з розміром радіуса основи циліндра і будують окружність у перспективі способом описаного квадрата за вісімью точкам. Для побудови висоти і верхньої основи циліндра застосовують вертикальну масштабну шкалу. Точки еліпса видимій частини нижньої основи переносять за допомогою горизонтальних прямих на масштабну шкалу. На ній визначають величину утворюючих циліндра і відзначають точки еліпса, які належать видимій частини верхньої основи циліндра.

Мал. 79

На картині (мал. 79) показана побудова гіпсової вази за дійсною величиною її профілю. Для цього задають обрис її форми в площині картини і будують вертикальну масштабну шкалу. На заданій глибині визначають висоту окремих частин вази а на горизонтальних прямих — розміри по ширині в перспективі. Потім відзначені розміри на масштабній шкалі переносять на вісь вази, яка задана на картині з урахуванням глибини її розташування. Мал. 80

На картині, одержавши розмір горизонтального діаметра окружності в кожній частині ширини вази, будують зображення квадратів і відзначають точки еліпса на видимій її поверхні. Збудувавши еліпси на різній висоті, малюють обрис зовнішньої форми вази в перспективі.

На картині (мал. 80) зображена кімната, одна стіна якої розташована фронтально. Потрібно зобразити круглий стіл і над ним лампу з циліндричним плафоном. Спочатку задають глибину вісі столу з основою у точці А и проводять через неї фронтальну площину, лінія перетинання якої зі стелею визначить місце прикріплення проводу лампи в точці В. За допомогою масштабної шкали відміряють висоту столу 0,75м, а на горизонтальній прямій —діаметр 1,2 м кришки столу. При відзначеному діаметрі і центріокружності будують на картині перспективу кришки столу способом описаного квадрата. Побудову плафона виконують аналогічно.

Площина окружності вертикальна. На картині (мал. 81) показана побудова аркового мосту з напівциліндричним обрисом при зданому радіусі окружності. Помітимо, що його окружності розташовані в глибинних площинах із точкою сходу Р. Звідси ширину арки (діаметр окружності) визначають за допомогою масштабу глибин із точкою сходу D для ліній переносу. Висота арки відповідає радіусу окружності. Цей розмір визначають за допомогою масштабу висот. Способом описаного квадрата будують точки еліпса та обрис арки моста. Помітимо, що товщина арки визначається горизонтальним відрізком прямої, паралельної основі картини за допомогою масштабу широт.

Мал. 81

Питання і вправи для самоконтролю

1. Як побудувати (і визначити) у перспективі кут, що лежить у предметній площині?

2. Як побудувати (і визначити) у перспективі кут нахилу прямої, що лежить у предметній площині, до основи картини?

3. Побудуйте в горизонтальній і вертикальній площинах (задавши розміри) геометричні фігури: квадрат, прямокутник, правильний трикутник і шестикутник. Вертикальну площину задайте глибинної і під довільним кутом до картині.

4. Побудуйте в перспективі по заданих розмірах у масштабі даної картини геометричні тіла: куб, паралелепіпед, трикутну і шестикутнупризми, бічні грані яких розташовані вертикально і горизонтально, правильну чотирикутну піраміду, яка стоїть основою на горизонтальній площині.

5. На картині (мал. 82 і 83) задані кути, по-різному розташовані щодо картинної і предметної площин. Визначите натуральний розмір цих кутів у масштабі даної картини.

Дата добавления: 2015-05-29