Приведенная форма МЭМ-1

Определение

Определение

Уравнение поведения, которое также называется уравнением реакции, описывает или объясняет поведение экономических субъектов или последствия этого поведения при определенных технических и организационных структурах. Числовые значения параметров уравнений поведения, как правило, неизвестные, их нужно определять в процессе оценки параметров.

Различают следующие уравнения поведения:

- уравнение поведения в более узком смысле.

То есть уравнения, которые объясняют поведения экономических объектов или тесно связанных с ними величин (функция предложения, функция опроса, уравнения формирования цен).

- технологические уравнения.

Они определяют прежде всего влияние технических условий на зависимую переменную.

- организационные уравнения.

Они отображают влияние организационных структур на эндогенную переменную. (Функция, которая определяет величину налога в зависимости от суммы дохода).

Тождество (расчетная тождество, балансовое тождество definitional equation) отличается от уравнения поведения двумя следующими особенностями:

1. Числовые данные коэффициентов объясняющих переменных известны к оценке параметров.

2. В тождестве отсутствуют возмущения.

Структурные уравнения взаимозависимой системы не могут использоваться отдельно для получения качественного прогноза взаимозависимых переменных.

Для прогнозирования взаимозависимых переменных модели необходимо относительно этих переменных решить структурные уравнения.

В эконометрии это значит получить приведенную (редуцированную) форму модели – прогнозную форму.

1. Приведенная форма функции потребления

, (3)

2. Приведенная форма балансового уравнения.

(4)

Причинные связи приведенной формы МЭМ-1.

Любое уравнение приведенной формы взаимозависимой системы может использоваться отдельно для прогноза зависимой переменной.

Однако относительно полную картину зависимости между наблюдаемыми переменными взаимозависимой модели получают лишь тогда, когда анализируют структурную и соответствующую ей приведенную форму.

Приведенная форма линейной взаимозависимой модели содержит мультипликаторы. Все мультипликаторы одного периода составляют матрицу.

В экономической теории, если речь идет о моделях Кейнса, она известна как матричный мультипликатор Кейнса.

Поскольку матричный мультипликатор содержит много мультипликаторов, то целесообразнее употреблять термин – мультипликаторная матрица.

Составим мультипликаторную матрицу для МЭМ-1.

П- мультипликаторная матрица 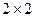статистической МЭМ-1.

Как интерпретируют эти мультипликаторы и как их называют?

показывает, на сколько единиц, при прочих равных условиях, изменяется і-я эндогенная переменная, если в этот же период экзогенная переменная изменяется на единицу.

является мультипликатором j-й экзогенной переменной 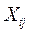относительно і-й эндогенной переменной .

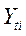Кратко: является мультипликатором .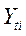

Мультипликаторы в МЭМ-1 выражают общий эффект действия объясняющих переменных на зависимые переменные, в отличие от структурных коэффициентов взаимозависимой модели, которые показывают частные, – эффекты такого действия.

Поэтому мультипликаторы имеют важные значения при получении информации для принятия решения.

Однако не все коэффициенты, как мультипликатор имеют экономический смысл. Например,переменная при нем (свободный член).

Дата добавления: 2015-05-26