Приведеная форма МЭМ-2

Преобразуем структурную форму.

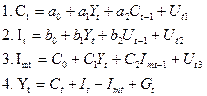
Подставим 1, 2, 3 в 4.

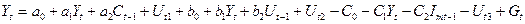
следовательно

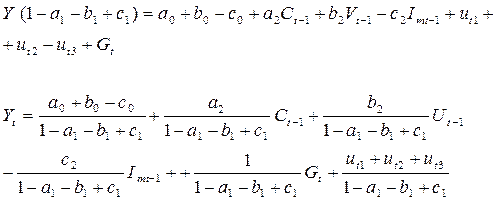
Подставим значение 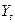в 1, 2, 3.

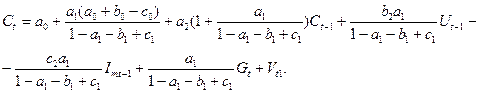
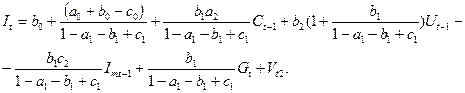
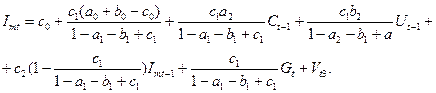
Следовательно, структурная форма МЭМ-2 приводится к виду:

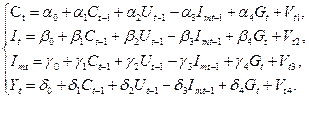
Здесь приняты обозначения

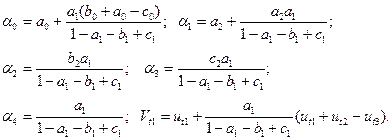
Структурные уравнения, в которых структурные коэффициенты 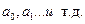оценены МНК-1 (на основе рядов данных).

Задание 5.

1) Получите уравнение приведенной формы МЭМ-2.

2) Из структурной и приведенной формы МЭМ-2 выпишите коэффициенты экзогенной переменной, которая не опаздывает 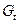(гос. расходы). Что можно сказать о реалистичности предположения относительно «других ровных условий» при интерпретации этих коэффициентов?

3) Назовите и интерпретируйте в МЭМ-2 мультипликаторы с нулевым лагом экзогенной переменной - государственные расходы. Используйте при этом точные обозначения переменных.

ВЫВОДЫ:

1. Для приведенной формы линейной эконометрической модели типичным является то, что ее уравнения не содержат незапаздывающих эндогенных переменных в качестве объясняющих.

2. В приведенной форме 20 коэффициентов отличающихся от нуля. В структурной форме только 9. Это подчеркивает важное обстоятельство: в приведенной форме эконометрической модели каждая эндогенная переменная зависит от большего количества факторов, чем предусматривается на основе соответствующей структурной формы.

3. Числовые значения коэффициентов экзогенных переменных, которые не запаздывают () в структурной и приведенной формах разные. Поэтому при анализе коэффициентов экспериментальных моделей необходимо указывать какие именно.

4. Коэффициенты незапаздывающихэкзогенных переменных в приведенной форме является мультипликаторами, которые действуют без запаздывания (= мультипликаторы с нулевым лагом), мультипликаторы первоначального действия.

5. Коэффициенты запаздывающих эндогенных и запаздывающих экзогенных переменных не является мультипликаторами в экономико теоретическом смысле. Эти коэффициенты выражают лишь степень влияния (частичный эффект) переменных предыдущего периода на соответствующую эндогенную переменную.

Объяснение: экзогенные переменные предыдущего периода влияют через коэффициенты незапаздывающих экзогенных переменных на зависимые переменные уравнений в том же предыдущем периоде. Эти зависимые переменные предыдущего периода в свою очередь влияют на незапаздывающие зависимые переменные текущего периода. К этому добавляется эффект влияния экзогенных переменных предыдущего периода через коэффициенты запаздывающих экзогенных переменных на незапаздывающие эндогенные переменные текущего периода. Все частичные эффекты складываются и создают общий эффект.

Такие эффекты называются динамическими мультипликаторами.

Эти мультипликаторы на практике используются для исследования экономических показателей как в прогнозном периоде, так и в пределах предыстории (ретроспективные исследования).

Причинные связки приведенной формы МЭМ-2

Дата добавления: 2015-05-26