Случайные составляющие коэффициентов регрессии

Свойства коэффициентов регрессии и проверка гипотез

С помощью регрессионного анализа мы можем получить оценки параметров зависимости. Однако они являются лишь оценками, потому возникает вопрос о том, насколько они надежны.

Коэффициент регрессии, вычисленный методом наименьших квадратов, - это особенная форма случайной величины, свойства которой зависят от свойств остаточного члена в уравнении.

Рассмотрим модель парной регрессии.

и на основе n выборных наблюдений будем оценивать уравнение регрессии

.

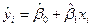Мы также будем допускать, что х- это случайная экзогенная переменная. То есть ее значение во всех наблюдениях можно считать предварительно заданными, в содержит две составляющие и

- неслучайная составляющая

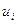- случайная составляющая.

Отсюда следует, что, когда мы вычисляем 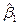по обычной формуле:

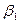также содержит случайную составляющую.

(x,y) зависит от в, а в зависит от u.

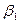Для разных наборов из n наблюдений получим разные величины (x,y) и следовательно . То есть оценка 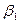- случайная величина, которая меняется от выборки к выборке.

Теоретически мы можем разложить 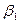на случайную и неслучайную составляющие

Таким образом_

, (5)

Следовательно, коэффициент регрессии, полученный по любой выборке, представляется в виде двух слагаемых:

1. Постоянной величины, ровной действительному значению .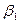

2. Случайной составляющей, зависимой от (x,u), которой обусловлены отклонения коэффициента .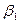

Аналогично можно показать для константы .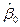

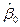. Таким образом состоит из

1. Постоянной составляющей, ровной действительному значению .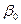

2. Случайной составляющей, которая зависит от случайного фактора u.

Следует заметил, что на практике мы не можем разложить коэффициенты регрессии составляющие, поскольку не знаем действительных значени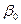й и 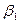или фактических значений 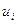в выборке. Они интересуют нас потому, что при определенных предположениях позволяют получить некоторую информацию о теоретических свойствах 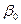и .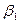

Дата добавления: 2015-05-26