Допустимо, что мы оценили модель

Действительные точечные и интервальные прогнозы (прогнозы) регрессанда в классической модели регрессии.

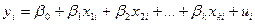(1)

На наблюдениях периода (i=1.n)

Имея некоторые послевыборочные значение переменных, мы можем предусмотреть соответствующее значение для некоторого периода i+p.

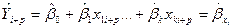(2)

(Рассчитанные из уравнения регрессии 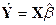(3) для выборочных значений 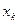оценки регрессанда 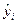не будет, строго говоря, действительно прогнозами, они являются ex-post-прогнозами).

Об истинно прогнозах(=ex-ante-прогнозах) регрессанда говорят тогда, когда во временных рядах прогнозный период лежит после оценочного периода, то есть вне базового временного периода. При обработке пространственных рядов действительный прогноз имеет место в том случае, если он относится не к n элементам выборок. а к другим элементам. что находится за ее пределами, но что относится к той же генеральной совокупности данных.

Истинно прогнозы могут быть важными по следующим причинам:

Некоторые эконометристы изучают экономические закономерности с целью улучшить понимание того, как работает экономика, но для других это является средством достижения более практической цели – предусматривать, что может случиться. Во многих странах макроэкономическое прогнозирование имеет высокую репутацию, и коллективы экономистов поддерживаются министерством финансов или другими правительственными органами, частными финансовыми учреждениями, университетами и исследовательскими институтами, и их прогнозы активно используются для формирования и толкования государственной политики или в деловых целях.

Однако есть и другое приложение эконометрического прогнозу, который делает его предметом беспокойства большинства эконометристов независимо от того заняты они прогнозированием или нет. Оно дает метод оценки стойкости регрессионной модели, который имеет большую исследовательскую направленность, чем диагностические статистики, которые использовались до сих пор.

Качество прогноза будет тем выше, чем

- полнее выполняются предпосылки модели в прогнозный часовой период;

- надежнее (достоверно) оценены параметры модели;

- точнее определены значения регрессоров для прогнозного временного периода.

Необходимо различать два понятия:

прогноз математического ожидания регрессанда и прогноз индивидуального значения регрессанда.

Значение 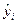(точечное оцененное значение), вычисленное по формуле (2) по заданному вектору 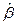и вектору значений регрессоров 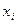может быть:

1) оценку такого параметра модели, как математического ожидания 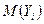регрессанда (средний прогноз).

2) оценку индивидуального значения 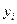регресснда, то есть оценку реализации .

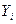При получении прогноза (1) мат. ожидание 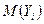учитывается предпосылка 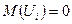. При расчете прогноза (2) необходимо было бы прибавить в формулу (2) прогнозное значение реализации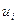 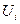. Из-за отсутствия отдельного оцененного значения 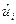в этом случае также допускают 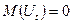и берут его как оценено значение .

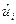Дата добавления: 2015-05-26