Перенос груза

Пусть на судне некоторый груз P массой m перенесен так, что ЦТ этого груза переместился из точки с координатами x ₀, y_{­ 0}, z ₀ в точку с координатами x ₁, y_­1, z ₁. Тогда масса всего судна не изменится, но изменится положение его ЦТ. Разлагая фактическое перемещение ЦТ груза на три взаимно перпендикулярных перемещения, параллельные координатным осям, рассматриваем продольное перемещение l_x = x ₁ — x ₀ поперечное перемещение l_y = y ₁ — y ₀ и вертикальное перемещение l_z = z ₁ — z ₀ (рис. 1).

Перемещение ЦТ судна можно найти с помощью теоремы теоретической механики о статических моментах, согласно которой

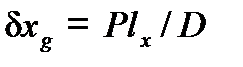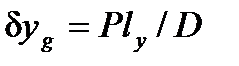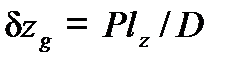; ; . (1)

Благодаря этому перемещению появятся две дополнительные пары сил. Одна из них будет действовать в ДП, вызывая дифферент. Плечо ее будет равно 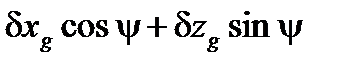. Другая же будет действовать в поперечной плоскости, параллельной плоскости мидель-шпангоута, вызывая крен. Плечо ее будет равно 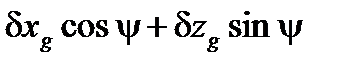. Моменты этих пар равны:

дифферентующий

;

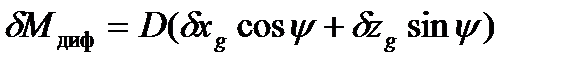кренящий

.

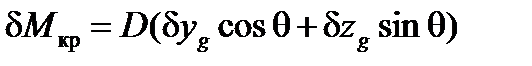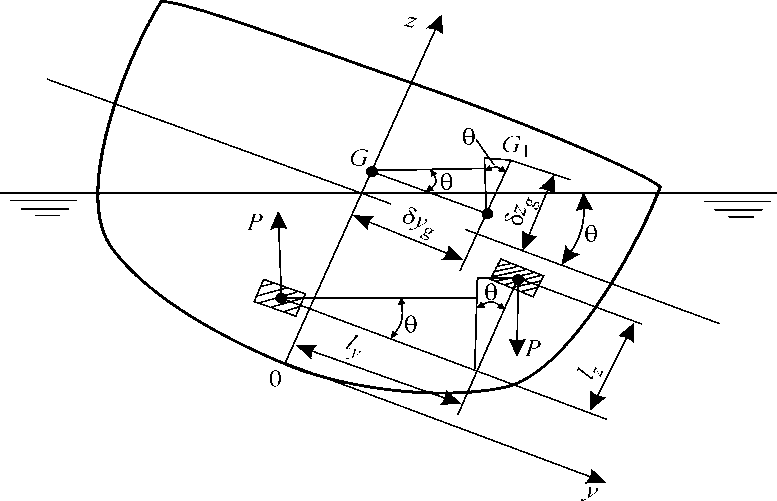
Рис. 1. Кренящая пара сил при переносе груза

Подставляя в эти формулы выражения (1), получим

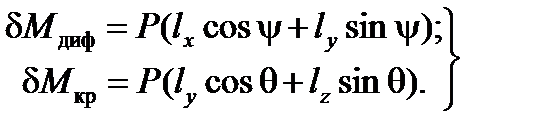(2)

Будем считать, что углы наклонения судна достаточно малы, так что 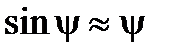; ; 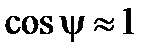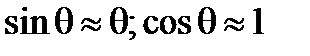. Тогда формулы (2) принимают вид:

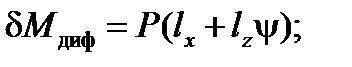
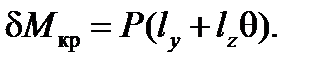(3)

Согласно условиям равновесия действие этих моментов уравновесится действием восстанавливающих моментов. Определим последние по метацентрическим формулам остойчивости:

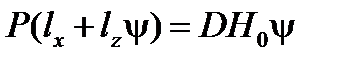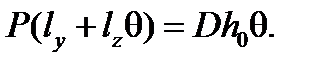; . (4)

Отсюда угол дифферента, возникающий вследствие переноса груза, равен

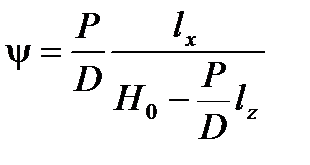, (5)

а угол крена

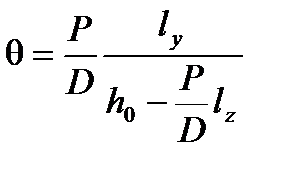. (6)

Выражения для метацентрических высот, измененные из-за влияния переноса груза, будут следующие:

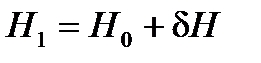; (7)

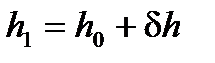, (8)

где поправки к метацентрическим высотам оказываются одинаковыми;

.

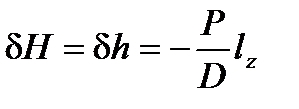Для большинства судов продольная метацентрическая высота намного больше поперечной. Поэтому в практических расчетах поправкой 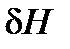почти всегда можно пренебречь по сравнению с 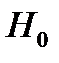и положить 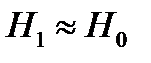. Тогда, подставив (7) и (8) в формулы (5) и (6), окончательно найдем

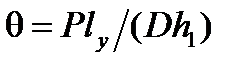; .(9)

Если груз переносится в нос, то 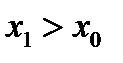, , 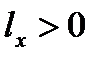а значит и 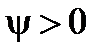, т. е. судно получает дифферент на нос. Если же груз переносится в корму, то 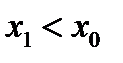, , 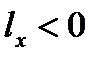, 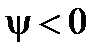т. е. судно дифферентуется на корму. В случае переноса груза на правый борт 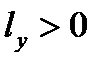и 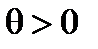, а в случае переноса на левы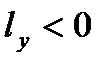й и .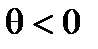

Дата добавления: 2015-06-04