Определение координат центра величины и метацентра при больших наклонениях

МОДУЛЬ 7. ОСТОЙЧИВОСТЬ НА БОЛЬШИХ УГЛАХ КРЕНА

При больших углах крена метацентрические формулы остойчивости нельзя использовать, так как величина метацентрического радиуса не будет постоянной во время наклонения, а будет меняться из-за изменения момента инерции площади ватерлинии. Метацентр также будет менять свое положение в процессе наклонения. Метацентрический радиус при наклонении можно определить по формуле

, (1)

причем V= const, так как предполагается, что наклонения остаются равнообъемными. Вид кривой 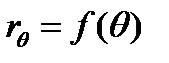представлен на рис. 1.

Рис. 1. Зависимость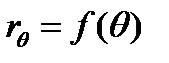

«Горбы» на графике соответствуют входу палубы в воду и выходу скулы из воды, касательная при θ = 0 горизонтальна, так как при малых отклонениях от θ = 0 момент инерции площади ватерлинии меняется слабо.

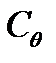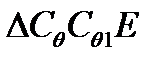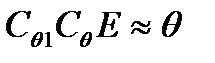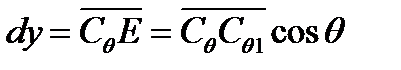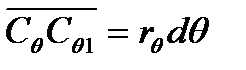С помощьюрис. 2 определим координаты ЦВво время наклонения. Сначала получим выражения для бесконечно малых перемещений точки dy и dz при отклонении судна от заданного угла θ на величину dθ. В угол , тогда из этого треугольника будет и , или, учитывая, что , получим и .

Если проинтегрировать эти перемещения за все время наклонения, то получится

(2)

Координаты метацентра будут равны

(3)

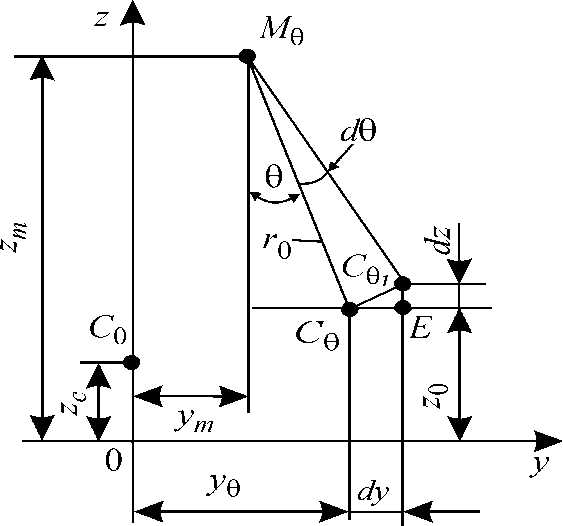
Рис. 2. Определение координат ЦТ во время наклонений

Дата добавления: 2015-06-04