Задачи, решаемые с помощью диаграмм статической остойчивости

Практические задачи, решаемые с помощью диаграмм статической и динамической остойчивости

Задач, которые решаются с помощью диаграмм статической и динамической остойчивости очень много, но ввиду ограниченности времени изучения дисциплины мы приводим только основные. Для студентов, интересующихся этим вопросом, преподаватель может пореко-мендовать соответствующую литературу.

Предположим, что на судно действует момент М_кр, не зависящий от угла крена. На диаграмме моментов (рис. 4) он будет изображаться прямой линией, которая пересекается с кривой восстанавливающего момента M_в в точках А и В. Точки А и В являются точками статического равновесия, так как в них соблюдается равенство кренящего и восстанавливающего моментов М_кр = М_в.

Рис. 4. Определение статических углов крена при действии M_кр

В точке А угол θ₁ - угол устойчивого равновесия, так как, если судно вывести из положения равновесия в этой точке, увеличив, например, угол θ₁ на δθ, то, будучи предоставлено самому себе, судно под действием восстанавливающего моментавернется в прежнее положение. Если же вывести судно из положения равновесия, уменьшив угол на δθ, то оно под действием кренящего момента также вернется в прежнее положение. При этом в точке А

. (7)

В точке В угол θ₂ характеризует положение неустойчивого равновесия, так как, если вывести судно из положения равновесия, добавив δθ, кренящий момент будет больше восстанав-ливающего, и оно будет крениться дальше, пока не опрокинется. Если же θ₂ уменьшить на величину δθ, получится М_кр < М_в, и судно перейдет в положение равновесия θ₁. В точке В

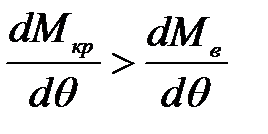. (8)

Таким образом, только угол θ₁ будет углом статического равновесия. Его обозначают θ_ст.

Если М_кр = М_max, точки А и В сольются в точке касания, получится безразличное равновесие, которое по определению не является остойчивым.

Судно может практически безопасно плавать в наклонном положении при углах, меньших θ_max, так как при углах крена, больших θ_max, всегда могут найтись такие внешние силы, которые переведут судно из положения равновесия к углу заката диаграммы, и оно опрокинется.

Максимальный кренящий момент М_кр = M_max, который судно может выдерживать не опроки-дываясь называется предельным статическим кренящиммоментом M_пр.ст. Соответствующий ему угол θ_max будет предельным статическим углом крена.

Разница между М_пр.ст и каким-либо статически приложенным моментом характеризует запас статической остойчивости судна.

В случае действия на судно динамически приложенного кренящего момента условием равновесия будет равенство не моментов, а равенство их работ Т_кр = Т_в, или

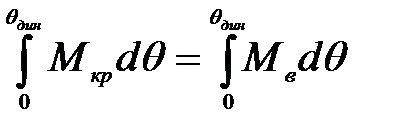, (9)

где θ_дин - угол крена, соответствующий углу динамического равновесия(рис. 5).

Угол θ_дин может определяться графически из следующих соображений. Интегралы являются площадями фигур ODFDEO и OACDEO, ограниченными сверху М_кр и М_в, а справа - абсциссой θ_дин и характеризуют работы соответствующих моментов. Уравнивая площади этих фигур, получаем θ_дин. Можно этот угол определить и более просто. Так как дважды заштрихованная площадь OADE0 – общая, можно уравнять площади треугольников ОВА и АCD (рис. 6).

Как мы видим, для одного и того же кренящего момента, но приложенного динамически или статически, динамический угол крена больше статического, т.е. θ_дин > θ_ст.

Максимальный динамически приложенный кренящий момент, который еще не опрокинет судно, определяется из условия приравнивания площадей ОВА и АCD так, чтобы не осталось незаштрихованных площадей между кренящим и восстанавливающим моментами (рис. 7). Этот кренящий момент называется предельным динамическим моментом М_.пр.дин. Предельный динамический момент меньше предельного статического момента, т.е. динамически прило-женный кренящий момент опаснее статически приложенного.

Разница между М_пр.дин и каким-либо динамически приложенным кренящим моментом характеризует запас динамической остойчивости.

Рис. 5. Определение θ_дин

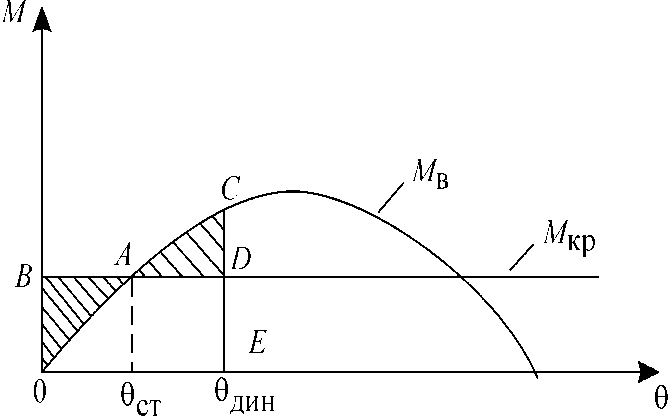
Рис. 6. Определение θ_дин по упрощенной модели

Рис. 7. Определение предельного динамического момента

Дата добавления: 2015-06-04