Задачи, решаемые с помощью диаграмм динамической остойчивости

С помощью диаграммы динамической остойчивости можно решить те же задачи, что и с помощью диаграммы статической остойчивости. Особенно удобно решать задачи об определении динамического угла крена θ_дин и предельного динамического момента М_пр.дин. Например, если кренящий момент не зависит от θ, работа кренящего момента будет равна,

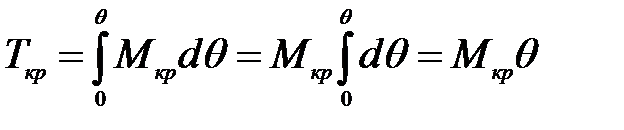, (10)

т.е. Т_кр - линейная функция от θ. Кстати, если θ =1 радиан, Т_кр = М_кр, что можно использовать для построения графика Т_кр (θ) (рис. 8). Работа восстанавливающего момента равна

. (11)

Динамический угол крена определится в точке пересечения T_кр и Т_в.

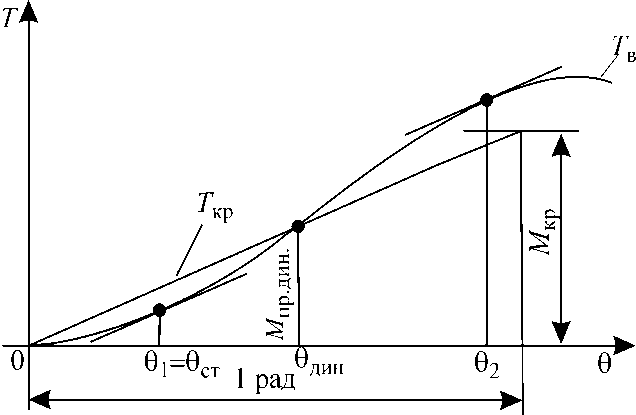
Рис. 8. Определение θ_дин и θ_ст на диаграмме динамической остойчивости

Статические углы крена определятся из равенства моментов, т.е.

.(12)

Следовательно, необходимо провести касательные к кривой Т_в параллельно прямой Т_кр. В точках касания будет θ₁ = θ_ст и θ₂.

Предельный динамический момент М_пр.дин можно определить, проведя касательную к кривой Т_в из начала координат и измеривординату на расстоянии 1 радиан от начала координат (рис. 9), а предельный статический момент - проведя касательную к кривой Т_в в точке перегиба А, соответствующей максимуму диаграммы статической остойчивости, и измерив на расстоянии 1 радиан ординату ВС, отсчитываемую от прямой АВ, параллельной оси абсцисс.

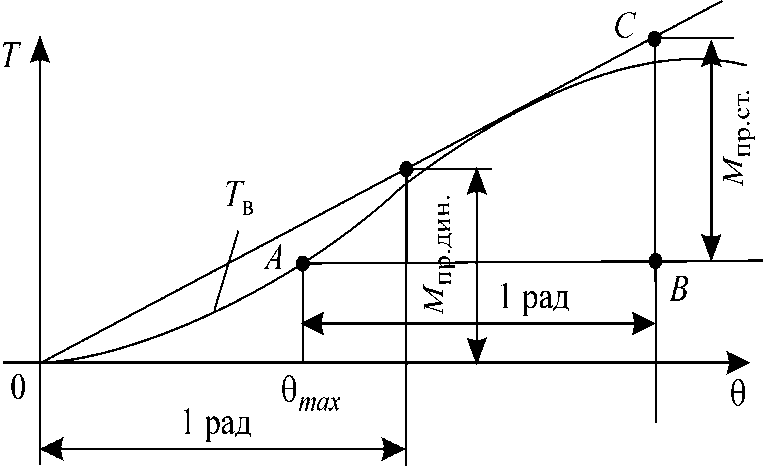
Рис. 9. Определение М_пр.ст и М_пр.дин с помощью диаграммы динамической остойчивости

Дата добавления: 2015-06-04