Метод МО

В этом методе молекула рассматривается в рамках орбитальной модели, точно так же, как многоэлектронный атом, только способы движения электронов описываются не атомными, а молекулярными орбиталями (МО). Молекулярная орбиталь отличается тем, что она является многоцентровой, т.е. охватывает сразу несколько атомных ядер.

Глобальная волновая функция молекулы в методе МО строится в виде определителя Слэтера, каждая строка которого включает все занятые электронами МО. Для этого, однако, необходимо знать явный вид МО. Эта задача решается на основе принципа суперпозиции — неизвестная функция заменяется линейной комбинацией известных базисных функций:

j _i = C_{i 1} y₁ + C_{i 2} y₂ + …

Для построения таких комбинаций в методе используется атомный базис, аналогичный тому, который применяется в методе ВС. Единственная разница заключается в том, что в методе ВС анализируется глобальная функция молекулы, а в методе МО — одноэлектронные молекулярные орбитали. В методе ВС с помощью перегородок разрезается многоэлектронное облако, включающее все электроны молекулы. В методе МО тем же набором перегородок разрезается одноэлектронное облако. Поэтому здесь в качестве резонансных форм выступает единственный электрон, локализованный в окрестности одного из ядер. Его движение в этом случае описывается соответствующей атомной орбиталью. В результате, каждая МО представляется в виде линейной комбинации базисного набора атомных орбиталей (ЛКАО).

Основная проблема метода МО сводится к вычислению коэффициентов разложения для каждой из МО. При решении этой задачи следует учитывать два важных условия.

1) ортонормированность: òj _i j _j dv = d _ij (1 при i = j и 0 при i ¹ j),

2) пространственная симметрия: j _i Ì НП ТГС (всякая МО должна описываться одним из типов симметрии точечной группы молекулы).

Для молекулы водорода принято классифицировать МО относительно операции инверсии — на четные, для которых i (j _g) = (+1)(j _g) и нечетные, для которых i (j _u) = (–1)(j _u).

Перейдем к рассмотрению молекулы водорода. Для нее атомный базис состоит всего из двух АО, которые обозначим, как и в методе ВС, буквами A и B. Тогда любая МО должна выражаться линейной комбинацией типа:

j = C _A × A + C _B × B

Учет симметрии молекулы приводит к условию: | C _A|² = | C _B|², которое выполняется в двух случаях: при C _A = + C _B и C _A = – C _B. Следовательно, можно построить всего две МО — одну четную (G) и одну нечетную (U):

G = C_g (A + B) и U = C_u (A – B)

Нормировочные множители можно найти стандартным путем:

C_g = 1 / (2 + 2 s)^1/2 и C_u = 1 / (2 – 2 s)^1/2

Дополнив полученные МО спиновыми множителями a или b, получим четыре варианта молекулярных спин-орбиталей (МСО): G a, G b, U a и U b.

При сближении атомов водорода их электроны, движущиеся по атомным типам А и В, вынуждены перейти к молекулярным типам движения, в качестве которых и выступают найденные четыре МСО. Поскольку электронов всего два, заселены будут только две из четырех МСО. Следовательно, существует несколько вариантов конечного состояния молекулы, а именно — шесть.

Номер состояния
состояние электрона № 1	Ga	Ga	Ga	Gb	Gb	Ua
состояние электрона № 2	Gb	Ua	Ub	Ua	Ub	Ub

Для каждого варианта можно построить глобальную волновую функцию в виде определителя Слэтера. Например, для первого варианта волновая функция будет иметь вид (без учета нормировочного множителя):

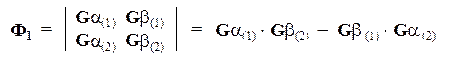
Запишем вид и остальных функций, придерживаясь стандартного соглашения (первый сомножитель относится к первому электрону, второй — к второму).

j1	j2	Глобальная волновая функция
Ga	Gb	Ф1 = Ga × Gb – Gb × Ga = [GG](ab – ba)
Ga	Ua	Ф2 = Ga × Ua – Ua × Ga = [GU – UG](aa)
Ga	Ub	Ф3 = Ga × Ub – Ub × Ga
Gb	Ua	Ф4 = Gb × Ua – Ua × Gb
Gb	Ub	Ф5 = Gb × Ub – Ub × Gb = [GU – UG](bb)
Ua	Ub	Ф6 = Ua × Ub – Ub × Ua = [UU](ab – ba)

Все эти волновые функции обладают нужной для выполнения принципа Паули перестановочной антисимметричностью. Глобальные волновые функции, однако, должны кроме этого, обладать и подходящей пространственной симметрией, например, быть либо четными, либо нечетными. Для проверки этой характеристики, необходимо отделить пространственную часть от спиновой и подействовать на пространственную часть оператором инверсии.

Из таблицы видно, что функции Ф₃ и Ф₄ не разделены на пространственный и спиновой сомножители. Поэтому для них невозможно определить тип симметрии. Обойти эту трудность можно посредством известного приема — симметризации — заменить неправильные функции Ф₃ и Ф₄ на их сумму и разность, обладающие правильной симметрией:

Ф'₃ = Ф₃ + Ф₄ = [ GU – UG ](ab + ba)

Ф'₄ = Ф₃ + Ф₄ = [ GU + UG ](ab – ba)

Теперь можно установить пространственную симметрию глобальных волновых функций:

Ф	Пространственный множитель	Тип симметрии	Спиновой множитель	S	MS
Ф1	GG	четный (g)	ab – ba
Ф2	GU – UG	нечетный (u)	aa		+1
Ф'3	GU – UG	нечетный (u)	ab + ba
Ф'4	GU + UG	нечетный (u)	ab – ba
Ф5	GU – UG	нечетный (u)	bb		–1
Ф6	UU	четный (g)	ab – ba

Видно, что волновые функции Ф₂, Ф'₃ и Ф₅ образуют триплет: их пространственные множители одинаковы, а спиновые состояния отличаются ориентацией вектора глобального спина молекулы.

Ф_u = (1/2)^0,5(GU – UG)[ C ₁(aa) + C ₂ (ab + ba) + C ₃(bb)]

Дата добавления: 2015-06-04