Орбитальные энергии

В методе МО важное значение имеют орбитальные энергии (e), каждая из которых равна энергии единственного электрона, образующего стационарное облако определенной формы (типа G, U и др.), распределенное вокруг всего ядерного остова молекулы.

Орбитальные энергии можно легко вычислить, зная явный вид МО. Например, для четной орбитали типа G = С _G (А + В) получим:

e_G = (C _G)² ò G ₍₁₎ * (Н ₁) G ₍₁₎ dv ₁ = (C _G)² ò(A + B)₁ * (Н ₁)(A + B)₁ dv ₁ =

= (C _G)² ò A ₁ * Н ₁A ₁ dv ₁ + ò A ₁ * Н ₁B ₁ dv ₁ + ò B ₁ * Н ₁A ₁ dv ₁ + ò B ₁ * Н ₁B ₁ dv ₁ =

= (C _G)² (a + b + b + a)

Аналогично, для нечетной орбитали U = С _U (А – В) получим:

e_U = (C _U)² (a – b – b + a)

С учетом явного вида нормировочных множителей:

С помощью приведенных выражений орбитальная энергия электрона представляется в виде суммы более простых вкладов — a (остовный интеграл) и b (резонансный интеграл).

Остовный интеграл a представляет собой энергию электрона, движение которого в пространстве искусственно ограничено пределами одного атома. Ясно, что в таких условиях движение электрона описывается некоторой атомной орбиталью, и он образует одноцентровое электронное облако, которое, однако, находится под кулоновским влиянием всех ядер молекулы:

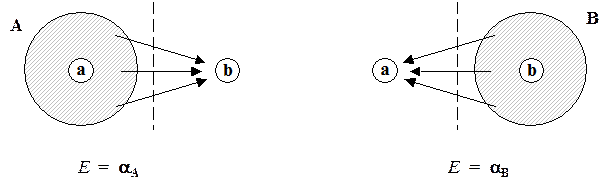
Для молекулы водорода оба остовных интеграла равны друг другу из-за симметрии молекулы (a_A = a_B). В случае несимметричных молекул разным атомам соответствуют и разные по величине остовные интегралы. Таким образом, остовные интегралы характеризуют химическую природу тех атомов, из которых построена молекула. Именно поэтому они особенно важны для решения химических задач.

Резонансные интегралы (b), в отличие от одноцентровых (одноядерных) остовных, являются двухцентровыми (двухядерными). Каждый такой интеграл характеризует определенную пару атомов в отношении их способности обмениваться электронами. Из вычислительной формулы:

b_AB = ò A* Н ₁B dv ₁ = á A | Н ₁ | B ñ

следует, что величина этого интеграла пропорциональная амплитуде вероятности некоторого события: электрон, локализованный в окрестности ядра b (на атомной орбитали B) с энергией a_B перейдет в аналогичное состояние возле другого атома (на атомную орбиталь А) с энергией a_А. Обратный переход характеризуется точно такой же амплитудой вероятности:

b_AB = á A | Н ₁ | B ñ = á В | Н ₁ | А ñ = b_BА

Поэтому нет необходимости рассматривать два разных резонансных интеграла для заданной пары атомов (это верно даже в случае разных по природе атомов).

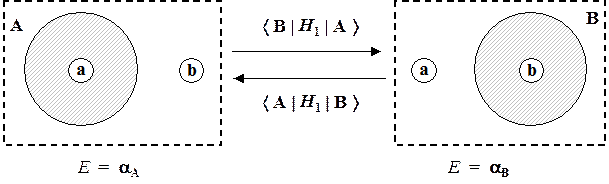
Резонансный интеграл имеет размерность энергии и представляет собой энергетическую поправку, смысл которой заключается в том, что электрон, способный переходить от одного атома к другому, обладает большей свободой и меньшей энергией, чем электрон, навсегда запертый в пределах одного из атомов (подобно тому, как энергия частицы, запертой в потенциальном ящике, уменьшается при увеличении размера ящика). Это означает, что все резонансные интегралы имеют отрицательные значения: b < 0.

Резонансные интегралы можно считать мерой интенсивности электронных взаимодействий между одноядерными фрагментами молекулы (т.е. химических связей между "химическими атомами").

Располагая выражениями для орбитальных энергий, можно построить еще одну энергетическую диаграмму, которая обычно называется корреляционной (КД). Фактически КД представляет собой две энергетические диаграммы — атомную и молекулярную. Первая показывает возможные состояния для электрона в исходных атомах, а вторая — возможные состояния того же электрона, но уже в молекуле. Для молекулы водорода КД имеет следующий вид:

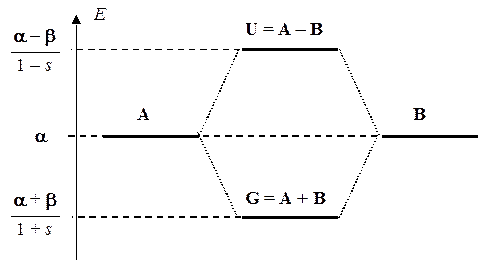
С помощью КД можно проследить изменения в энергии системы, которые сопровождают образование молекулы из атомов или, наоборот, ее разрушение. При образовании молекулы электроны с атомных орбиталей переходят на молекулярные, что сопровождается уменьшением полной энергии. При разрушении молекулы электроны локализуются на атомных орбиталях, что сопровождается увеличением полной энергии. Это увеличение энергии системы возможно только за счет внешних источников. Можно сказать, что разрушение молекул — это процесс всегда вынужденный, сопряженный с необходимостью затраты определенной порции энергии (энергии химической связи), величину которой можно легко рассчитать из КД. Другими словами, с помощью КД можно описывать не только сами молекулы, но и их химические превращения (реакции). Например, химической реакции Н + Н = Н₂ будет соответствовать КД:

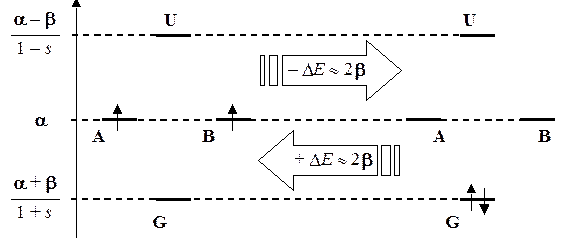
Левая часть диаграммы соответствует состоянию системы в виде двух отдельных атомов водорода (Н + Н), при этом оба электрона движутся по атомному типу (атомные орбитали А и В) и имеют энергию a. Правая часть соответствует состоянию системы в виде устойчивой молекулы (Н₂). Оба электрона движутся по молекулярному типу (молекулярные спин-орбитали Ga и Gb) и имеют энергии» a + b (т.к. s << 1). Следовательно, прочность химической связи в молекуле водорода можно приблизительно считать равной удвоенному значению резонансного интеграла (D Е» 2 b).

Дата добавления: 2015-06-04