Распределение наименьшей и наибольшей из нескольких СВ

Распределение наибольшей из нескольких СВ

Рис. 10.22. Область D_y = { x ₁, x ₂: max(x ₁, x ₂) < y }

Наибольшая из всех СВ системы (X ₁, …, X_n) задается функцией Y _max = max{ X ₁, …, X_n }. Событие (Y _max < y) наступает, когда все X_i меньше, чем y, т.е. представляет собой произведение независимых событий (рис. 10.22):

.

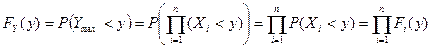(10.14)

Если все X_i подчиняются одному закону распределения F_X (x),

, .	(10.15) (10.16)

Распределение наименьшей из нескольких СВ

Рис. 10.23. Область D_y = { x ₁, x ₂: min(x ₁, x ₂) < y }

Функция Y _min = min{ X ₁, …, X_n } определяет наименьшую из всех СВ системы (X ₁, …, X_n). Событие (Y _min < y) наступает, когда хотя бы одна из X_i, меньше, чем y (рис. 10.23), т.е. представляет собой сумму независимых событий (X_i < y), i = 1, 2, …, n, вероятность которой можно определить через вероятность противоположного события:

.

(10.17)

Если все X_i подчиняются одному закону распределения F_X (x),

, .	(10.18) (10.19)

Построим законы распределения стандартного нормального закона, максимального и минимального значений из n = 20 таких СВ (рис. 10.24):

>> X=[-5:0.1:5]; F=p_Gauss(X); f=f_Gauss(X); n=20;

>> plot(X,[f; f.*n.*(1-F).^(n-1); f.*n.*F.^(n-1)],'r'), hold on,plot(X,[F;1-(1-F).^n; F.^n],'b')

Рис. 10.24. Графики нормального закона, максимального и минимального значений

Наименьший промах при круговом нормальном рассеивании

Из (10.18) видно, что функция распределения минимальной СВ имеет простой вид, если аргументы подчиняются законам Рэлея, Максвелла или показательному закону. Круговое нормальное рассеивание в картинной плоскости характеризуется параметром s. Наименьший промах в n независимых выстрелах R_n = min{ R ₁, …, R_n } подчиняется закону

.

(10.20)

Таким образом, наименьший из всех промахов в n независимых выстрелах с круговым нормальным рассеиванием s _x = s _y = s подчиняется закону Рэлея с параметром . Если поражение цели обеспечивается при одном попадании в круговую окрестность цели, можно заменить в расчетах n независимых выстрелов одним обобщенным выстрелом с СКО, равным .

Наиболее раннее событие из нескольких пуассоновских потоков

Время ожидания первого события в каждом из независимых потоков с плотностями l _i подчиняется показательному закону . Подстановка в (10.1) дает закон распределения времени ожидания первого из них:

.

Как и следовало ожидать, наиболее раннее событие из нескольких независимых потоков подчиняется тому же закону, что и первое событие в пуассоновском потоке с эквивалентной плотностью .

Контрольные вопросы

1. Какие законы распределения устойчивы по отношению к композиции? Что это значит?

2. Устойчиво ли к композиции равномерное распределение? Какому закону подчиняется сумма 12-и СВ, распределенных равномерно в интервале [0, 1]?

3. Какому закону подчиняется сумма двух нормально распределенных СВ X Î N (m ₁, s₁), Y Î N (m ₂, s₂)?

4. Чем объясняется отличие графиков закона Эрланга положительных порядков и показательного распределения при нулевом значении аргумента?

ПРИЛОЖЕНИЕ 10

Листинг 10.1. Файл-функция Para2_Distrib для построения закона распределения случайной площади проекции параллелепипеда:

function [Y,F]=Para2_Distrib(A,B,C)

topt=atan(B/C);

yopt=B*sin(topt)+C*cos(topt);

fopt=atan(A/yopt);

yopt=A*sin(fopt)+yopt*cos(fopt);

Y=linspace(A,yopt+3,300);

F=[];

for y=Y

F(end+1)=Para2_Proect_(y, A,B,C);

end

%

function out=Para2_Proect_(y, A,B,C)

out=0;

T=linspace(0,pi/2,100); dt=T(2)-T(1);T=T(2:end);

for t=T

b=B*sin(t)+C*cos(t);

ab2=A^2+b^2;

D=A^2*y^2-ab2*(y^2-b^2);

f2=0;

if D>0

D=sqrt(D);

f1 = (A*y-D)/ab2;

f2 = (A*y+D)/ab2;

if f1>0 out=out+f1; end

end

out=out+(1-f2);

end

out=out*2/pi*dt;

Листинг 10.2. Файл-функция Mid_S_Stat для построения статистического закона распределения случайной площади проекции многогранника:

function [U,F,f,maxW,L]=Mid_S_Stat(A,N,Gr)

if nargin<2 N=100000;end

s=rand(N,1)*2-1; s1=sqrt(1-s.^2);

v=rand(N,1)*2*pi;

D=[s1.*cos(v), s1.*sin(v), s];

n=size(A,1);W=0;L=zeros(N,1);

for i=1:n

d=D.*repmat(A(i,1:3),N,1); d=sum(d,2);

d(d<0)=0;

if nargout>4 L=max([L,d],[],2); end

d=d*A(i,4);

W=W+d;%disp(mean(sum(d,2)))

end

[f, F, U] = SDL(W,50); maxW=max(W);

Листинг 10.3. Файл-функция Mid_S:

function [f,F]=Mid_S(PG,N,K)

if nargin<2 N=50000;end

if nargin<3 K=50;end

fi=Gen('sin',-pi/2,pi/2,N);teta=Gen('rnd',0,2*pi,N);

[sq,n]=Facet(PG); PL=Plane([1 0 0]); S=zeros(1,N);

for i=1:N

d=Mdot(n,Normal(RotR(PL,2,fi(i),3,teta(i))));

I=find(d>0);

S(i)=dot(sq(I),d(I));

end

[f,F]=SmartHist(S,[],K);

Листинг 10.3. Скрипт-файл Lect10 для формирования матрицы проекций 8-гранника:

salfa=sin(alfa);calfa=cos(alfa); beta=atan(c/b);

h=c/(2*salfa);h1=sqrt(b^2+c^2)/2;a1=a-c*calfa/salfa;

St=b*h/2;Sb=(a+a1)/2*h1;

nob=[0 1 1; 0 1 -1; 0 -1 1; 0 -1 -1];

not=[1 0 1; 1 0 -1; -1 0 1; -1 0 -1];

A=[nob,ones(4,1)].*repmat([0 cos(beta) sin(beta) Sb],4,1);

A=[A;[not,ones(4,1)].*repmat([salfa 0 calfa St],4,1);

Листинг 10.4. Файл-функция f_Erlang для вычисления функции Эрланга:

% Плотность распределения Эрланга

% t - аргумент распределения

% L - плотность потока событий

% k - число пропущенных событий

%

function f= f_Erlang(t,L,k)

f=L/prod(1:k)*exp(-t*L).*(t*L).^k;

Дата добавления: 2015-06-25