Метод вырезания узлов

Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов фермы. Ход расчетов поясним на конкретном примере.

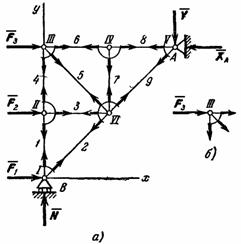
Рис.23

Рассмотрим изображенную на рис. 23,а ферму, образованную из одинаковых равнобедренных прямоугольных треугольников; действую­щие на ферму силы парал­лельны оси х и равны: F₁ = F₂ = F₃ = F = 2.

В этой ферме число узлов n = 6, а число стержней k = 9. Следовательно, соот­ношение выполняется и ферма является жесткой, без лишних стержней.

Составляя уравнения рав­новесия для фермы в целом, найдем, что реакции опор направлены, как пока­зано на рисунке, и численно равны;

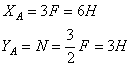
Переходим к определению усилий в стержнях.

Пронумеруем узлы фермы римскими цифрами, а стержни — арабскими. Искомые усилия будем обозначать S ₁ (в стержне 1), S ₂ (в стержне 2) и т. д. Отрежем мысленно все узлы вместе со сходящимися в них стержнями от осталь­ной фермы. Действие отброшенных частей стержней заменим силами, которые будут направлены вдоль соответствующих стержней и численно равны искомым усилиям S ₁, S ₂,... Изображаем сразу все эти силы на рисунке, направляя их от узлов, т. е. считая, все стержни растя­нутыми (рис. 23, а; изображенную картину надо представлять себе для каждого узла так, как это показано на рис. 23, б для узла III). Если в результате расчета величина усилия в каком-нибудь стержне получится отрицательной, это будет означать, что данный стержень не растянут, а сжат. Буквенных обозначений для сил, действующих вдоль стержней, ни рис. 23 не вводам, поскольку ясно, что силы, действующие вдоль стержня 1, равны численно S ₁, вдоль стержня 2 — равны S ₂ и т. д.

Теперь для сил, сходящихся в каждом узле, составляем последо­вательно уравнения равновесия

Начинаем с узла 1, где сходятся два стержня, так как из двух уравнений равновесия можно определить только два неизвестных усилия.

Составляя уравнения равновесия для узла 1, получим

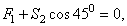
Отсюда находим

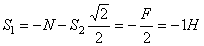
Теперь, зная S ₁, переходим к узлу II. Для него уравнения равнове­сия дают

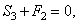
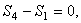
откуда

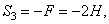
Определив S ₄, составляем аналогичным путем уравнения равновесия сначала для узла III, а затем для узла IV. Из этих уравнений находим:

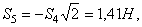
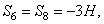
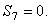
Наконец, для вычисления S ₉ составляем уравнение равновесия сил, сходящихся в узле V, проектируя их на ось By. Получим 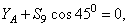откуда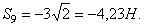

Второе уравнение равновесия для узла V и два уравнения для узла VI можно составить как поверочные. Для нахождения усилий в стержнях эти уравнения не понадобились, так как вместо них были использованы три уравнения равновесия всей фермы в целом при определении N, Х_А, и Y_А.

Окончательные результаты расчета можно свести в таблицу:

№ стержня..........
Усилие в Н.........	-1	-2,82	-2	-1	+1,41	-3		-3	-4,23

Как показывают знаки усилий, стержень 5 растянут, остальные стер­жни сжаты; стержень 7 не нагружен (нулевой, стержень).

Наличие в ферме нулевых стержней, подобных стержню 7, обна­руживается сразу, так как если в узле, не нагруженном внешними силами, сходятся три стержня, из которых два направлены вдоль одной прямой, то усилие в третьем стержне равно нулю. Этот результат получается из уравнения равновесия в проекции на ось, перпендикулярную к упомянутым двум стержням.

Если в ходе расчета встретится узел, для которого число неизве­стных больше двух, то можно воспользоваться методом сечений.

Метод сечений (метод Риттера).

Этим методом удобно пользоваться для определения усилий в отдельных стержнях фермы, в ча­стности, для проверочных расчетов. Идея метода состоит в том, что ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в одном из которых) требуется определить усилие, и рассматривают равновесие одной из этих частей. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, т. е. считая стержни растянутыми (как и в методе вырезания узлов). Затем составляют уравнения равновесия, беря центры моментов (или ось проекций) так, чтобы в каждое уравнение вошло только одно неизвестное усилие.

Дата добавления: 2015-06-04