Графический расчет плоских ферм

Расчет фермы мето­дом вырезания узлов может производиться графически. Для этого сначала, определяют опорные реакции. Затем, последовательно отсекая от фермы каждый из ее узлов, нахо­дят усилия в стержнях, сходящихся в этих узлах, строя соответствую­щие замкнутые силовые многоугольники. Все построения проводятся в масштабе, который должен быть заранее выбран. Рас­чет начинают с узла, в котором сходятся два стержня (иначе не удастся определить неизвест­ные усилия).

Рис.24

В качестве примера рассмотрим ферму, изображенную на рис. 24, а. В этой ферме число узлов n = 6, а число стержней k = 9. Следовательно, соотношение выполняется и ферма является жесткой, без лишних стержней. Опорные реакции и для рассматри­ваемой фермы, изображаем на­ряду с силам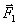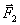и , и , как известные.

Определение усилий в стержнях начинаем с рас­смотрения стержней, сходящихся в узле I (узлы нумеруем римскими цифрами, а стержни - арабскими). Мысленно отрезав от этих стержней остальную часть фермы, отбрасываем ее действие отброшенной части также мысленно заменяем силами и 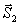, которые должны быть направлены вдоль стержней 1 и 2. Из сходящихся в узле I сил , и 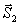строим замкнутый треугольник (рис. 24, б). Для этого изображаем сначала в выбранном масштабе известную силу , а затем проводим через ее начало и конец прямые, параллельные стерж­ням 1 и 2. Таким путем будут найдены силы и 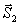, действующие на стержни 1 и 2. Затем рассматриваем равновесие стержней, сходящихся в узле II. Действие на эти стержни отброшенной части фермы мысленно заменяем силам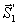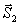и , , и 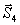, направленными вдоль соответствующих стержней; при этом сила нам известна, так как по равенству дей­ствия и противодействия 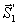= - . Построив из сил, сходящихся в узле II, замкнутый треугольник (начиная с силы 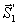), найдем вели­чины S ₃ и S ₄ (в данном случае S ₄ = 0). Аналогично находятся усилия в остальных стержнях. Соответствующие силовые многоугольники для всех узлов показаны на рис. 24, б. Последний много­угольник (для узла VI) строится для про­верки, так как все входящие в него силы уже найдены.

Из построенных многоугольников, зная масштаб, находим величины всех усилий. Знак усилия в каждом стержне опреде­ляется следующим образом. Мысленно вы­резав узел по сходящимся в нем стержням (например, узел III), прикладываем к обрезам стержней найденные силы (рис. 25); сила, направленная от узла (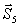 на рис. 25), растягивает стержень, а си­ла, направленная к узлу ( 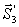и 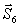на рис. 25) сжимает его.

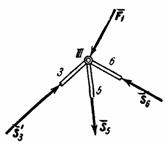
Рис.25

Согласно принятому условию растягивающим усилиям приписываем знак «+», а сжимающим - знак «-». В рассмотренном примере (pиc. 25) стержни 1, 2, 3, 6, 7, 9 сжаты, а стержни 5, 8 растянуты.

Дата добавления: 2015-06-04