Генетические операторы

Особые процедуры репродукции

В качестве особых процедур репродукции можно рассматри­вать так называемую элитарную стратегию и генетический алго­ритм с частичной заменой популяции.

Элитарная стратегия (elitist strategy) заключается в защите наилучших хромосом на последующих итерациях. В классическом ге­нетическом алгоритме самые приспособленные особи не всегда пе­реходят в следующее поколение. Это означает, что новая популяция Р(к + 1) не всегда содержит хромосому с наибольшим значением функции приспособленности из популяции Р(к). Элитарная стратегия применяется для предотвращения потери такой особи. Эта особь га­рантированно включается в новую популяцию.

Генетический алгоритм с частичной заменой популяции, ина­че называемый генетическим алгоритмом с зафиксированным со­стоянием (steady-state), характеризуется тем, что часть популяции переходит в следующее поколение без каких-либо изменений. Это означает, что входящие в эту часть хромосомы не подвергаются опе­рациям скрещивания и мутации. Часто в конкретных реализациях ал­горитма данного типа на каждой итерации заменяются только одна или две особи вместо скрещивания и мутации в масштабе всей попу­ляции. Именно такой подход принят, например, в программе Evolver [49]. В других программах, в частности, во FlexTool [48], пользователь

может сам установить - какая часть популяции (в соответствии со значениями функции приспособленности) должна передаваться без изменений в следующее поколение. Это подмножество хромосом не подвергается регулярной селекции и без изменений включается в но­вую популяцию

В классическом генетическом алгоритме операция скрещива­ния представляет собой так называемое точечное скрещивание, рас­смотренное в разд. 4.4 и в примерах 4.4 и 4.5. Также применяются и другие виды скрещивания: двухточечное, многоточечное и равно­мерное [9, 15].

Двухточечное скрещивание (two-point crossover), как следует из его названия, отличается от точечного скрещивания тем, что по­томки наследуют фрагменты родительских хромосом, определяемые двумя случайно выбранными точками скрещивания. Для пары хромо­сом из примера 4.4 скрещивание в точках 4 и 6 показано на рис. 4.12. Обратим внимание, что такое скрещивание не приводит к уничтоже­нию схемы -|**********1, которую представляет родитель 2.

Многоточечное скрещивание (multiple-point crossover) пред­ставляет собой обобщение предыдущих операций и характеризуется соответственно большим количеством точек скрещивания. Например, для трех точек скрещивания, равных 4, 6 и 9, и такого же количества родителей, как на рис. 4.12, результаты скрещивания показаны на рис. 4.13.

Аналогично производится скрещивание для пяти или больше­го нечетного количества точек. Очевидно, что одноточечное скрещи­вание может считаться частным случаем многоточечного скрещива­ния.

Пример двухточечного скрещивания, представленный на рис. 4 12 можно проиллюстрировать способом, показанным на рис. 4.14.

Многоточечное скрещивание для четырех точек, равных 1,4,6, 9 и 4, 6, 9, 11 для той же пары родителей из предыдущих примеров иллюстрируется на рис. 4.15.

Многоточечное скрещивание с большим четным количеством точек скрещивания протекает аналогично показанному на рис. 4.15.

Скрещивание с нечетным количеством точек можно предста­вить таким же образом, если добавить еще одну точку скрещивания в позиции, равной 0. Приведенный выше пример для трех точек можно представить также, как на рис. 4.15, с точками скрещивания 0, 4, 6, 9. При четном количестве точек хромосома рассматривается как замк­нутое кольцо (см. рис. 4.14 и 4.15), а точки скрещивания выбираются с равной вероятностью по всей его окружности.

Равномерное скрещивание (uniform crossover), иначе называе­мое монолитным или одностадийным, выполняется в соответствии со случайно выбранным эталоном, который указывает, какие гены долж ны наследоваться от первого родителя (остальные гены берут­ся от второго родителя). Допустим, что для пары родителей из приме-

4.8. Модификации классического генетического алгоритма

		эва 4. Генетическш	> алгоритмы
родител родител	ь 1: [001100111010] | ^CKP^aH"^Bf°^Kь 2: [101011011011] } 1к.4 6	[001111111010] пот [101000011011]: пот	OMOKl
Рис. 4.12. Пример двухточечного скрещивания.
родите родите	ль1:[001100Ш010] 1 скрещиваш ль2: [101011011011] | 1к:4 6 9	[001111111010]: по [101000011011]: по

Рис. 4.13. Пример трехточечного скрещивания

скрещивания 4 и 6.

Рис. 4.14. Двухточечное скрещивание

ров на рис. 4.12 - 4.15 выбран эталон 010110111011, в котором 1 оз­начает принятие гена на соответствующей позиции (locus) от родите­ля 1, а 0 - от родителя 2. Таким образом формируется первый пото­мок. Для второго потомка эталон необходимо считывать аналогично, причем 1 означает принятие гена на соответствующей позиции от ро­дителя 2, а 0 - от родителя 1. В этом случае равномерное скрещива­ние протекает так, как показано на рис. 4.16.

Оператор инверсии. Холланд [21] предложил три технологии для получения потомков, отличающихся от родительских хромосом. Это уже известные нам операции скрещивания и мутации, а также операция инверсии. Инверсия выполняется на одиночной хромосоме; при ее осуществлении изменяется последовательность аллелей меж­ду двумя случайно выбираемыми позициями (locus) в хромосоме. Не­смотря на то, что этот оператор был определен по аналогии с биоло­гическим процессом хромосомной инверсии, он не слишком часто применяется в генетических алгоритмах. В качестве примера выпол­нения инверсии рассмотрим хромосому [001100111010] и допустим, что выбраны позиции 4 и 10. Тогда в результате инверсии получим [001101110010].

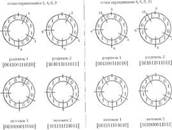
Рис. 4.15. Многоточечное скрещивание с четыры\ равными 1,4, 6, 9 и 4, 6, 9, 11.

[101101111010]: г [001010011011]: г

родитель 1: [001100111010] 1 родитель2: [101011011011] J

Рис. 4.16. Пример равномерного скрещивания.

4.8.4. Методы кодирования

В классическом генетическом алгоритме применяется двоич­ное кодирование хромосом. Оно основано на известном способе за­писи десятичных чисел в двоичной системе, где каждый бит двоично­го кода соответствует очередной степени цифры 2. Например, двоич­ная последовательность [10011] представляет собой код числа 19, по­скольку 1*2⁴ + 0*2³ + 0*2² + 1*2¹ + 1*2° = 19. Такой способ кодирова­ния применялся в примерах 4.1 и 4.5. Для кодирования действитель­ных чисел х, е [a,-, b] e R реализуется отображение (4.5) так, как это делалось в примерах 4.2 и 4.6.

В генетических алгоритмах можно, например, использовать код Грея, который характеризуется тем, что двоичные последовательное-

а 4. Генетические алгоритмы

4.8. Модификации классического генетического алгоритма

ти, соответствующие двум последовательным целым числам, отлича­ются только одним битом. Такой способ кодирования хромосом может оказаться оправданным при использовании операции мутации [8].

Логарифмическое кодирование (logarithmic coding) применяет­ся в генетических алгоритмах для уменьшения длины хромосом. Оно используется, главным образом, в задачах многомерной оптимизации с большими пространствами поиска решений.

При логарифмическом кодировании первый бит (а) кодовой по­следовательности - это бит знака показательной функции, второй бит Q3) - бит знака степени этой функции, а остальные биты (bin) пред­ставляют значение самой степени:

где [bm]₁₀ означает десятичное значение числа, закодированного в виде двоичной последовательности bin. Например,

[10110]

представляет собой кодовую последовательность числа х₁ = (-1)^о_е<-¹)¹[^11О]ю _{= е}-«₌ 0,002478752,

[01010] представляет собой кодовую последовательность числа

х₂ =(-i)¹e^M)°^[010li° =-e² =-7,389056099

Заметим, что таким образом с помощью пяти битов можно за­кодировать числа из интервала [-е⁷, е⁷]. Это значительно больший интервал, чем [0, 31] из примера 4.5. Логарифмическое кодирование было реализовано в программе FlexTool [48] в качестве дополнитель­ной опции для задач повышенной сложности.

Еще одна модификация классического генетического алгорит­ма основана на кодировании действительными, а не двоичными чис­лами. Это означает, что гены хромосом принимают действительные значения (аллели являются действительными числами). Такой спо­соб кодирования применяется, в частности, в программе Evolver [49].

Дата добавления: 2015-06-04