Приклади виконання завдання

Приклад1. Дано: G=2 кН; Q₁=20 кН; f_зч.=0,1; a=20°, а=10см; в=20см (рис.6.11). Визначити критичне значення сили Р і реакції опор О, А, В і С.

Рисунок 6.11

Розв’язання. Розглянемо систему врівноважених сил, що прикла-

дені до тіла вагою (рис.6.12). На тіло діють сила ваги , реакція Т і нормальна реакція .

Нехтуючи розмірами, розглянемо досліджуване тіло як матеріальну точку і складемо рівняння рівноваги вказаних сил:

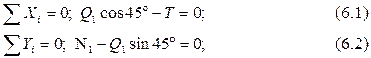
Звідси

Рисунок 6.12

Потім розглянемо рівновагу сил, прикладених до барабана (рис.6.13);

де 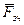– сила зчеплення (сила тертя спокою); (блок С –ідеальний).

Рисунок 6.13 Рисунок 6.14

Рисунок 6.1

Рисунок 6.2

Рисунок 6.3

Рисунок 6.4

Рисунок 6.5

Рисунок 6.6

Рисунок 6.7

Рисунок 6.8

Рисунок 6.9

Рисунок 6.10

В стані граничної рівноваги сила Р мінімальна, а сила зчеплення (тертя спокою) між гальмівною колодою і барабаном визначається рівністю

. (6.6)

З рівнянь (6.3)– (6.6) отримаємо:

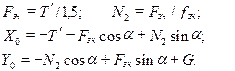
Для визначення мінімального значення сили P і реакцій опори А і В (ці реакції перпендикулярні направляючим А і В, тому що тертям в точках А і В нехтуємо) розглянемо рівновагу сил, прикладених до штока гальмівного пристрою (рис. 6.14):

Розв’язуючи отримані рівняння, маємо

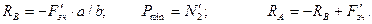
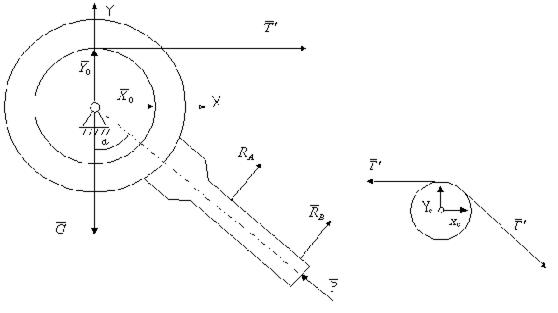
Рисунок6.15 Рисунок 6.16

Враховуючи задані в умові числові значення, отримаємо:

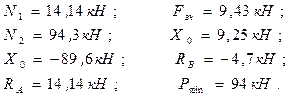
Для перевірки достовірності розв’язку розглянемо рівновагу сил, прикладених до барабана та штока як єдиної механічної системи (рис.6.15)

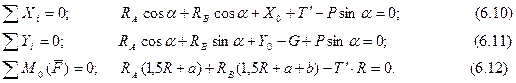
Так, наприклад, з врахуванням знайдених значень R_A, R_B і X₀ з формули (6.10) маємо:

14,1cos20^о-4,72cos20^о+9,25+14,14-94sin20^о=-0,01.

Для визначення реакції опори С достатньо скласти рівняння рівноваги сил, прикладених до блока (рис.6.16)

Розв’язуючи рівняння (6.13) і (6.14), знаходимо:

Приклад 2. Дано G=1кН; f_зч=0,4; a=6м; в=2м (рис.6.17). Визначити значення сили Р і реакції в точках А,В,D і Е при критичній рівновазі конструкції.

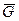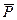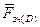Розв’язання. Розглянемо спочатку систему врівноважених сил, прикладених до тіла вагою G (рис.6.18). До тіла прикладена сила ваги , сила , нормальні складові реакції і , а також дотичні складові сили зчеплення і 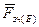(сили тертя спокою).

Рисунок 6.17 Рисунок 6.18

Складемо три рівняння рівноваги вказаних сил (рис 6.18):

У випадку граничної рівноваги 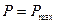. У цьому випадку сили зчеплення (сили тертя спокою) приймають екстремальні значення, а система рівнянь (6.15)-(6.17) доповнюється рівностями:

Розв’язуючи систему рівнянь (6.15)-(6.19), отримаємо:

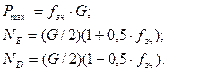
Звідки, з врахуванням числових даних маємо:

Сукупність і , і 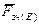створюють відповідно опорні реакції в точках D і Е.

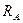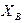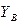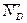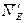Розглянемо рівновагу тіла АВ (рис.6.19). До нього прикладені реакції в’язей , , , нормальні складові реакції і , а також дотичні складові сили зчеплення і

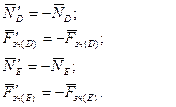
Складемо три рівняння рівноваги вказаних сил:

Розв’язуючи (6.20)-(6.22), отримаємо:

Звідки:

Для того, щоб впевнитись в достовірності розв’язку, розглянемо рівновагу системи сил 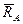, , , , 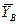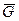і 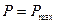прикладених до всієї системи (рис 6.10):

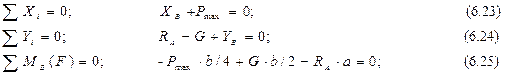
Розв’язуючи рівняння (6.23)-(6.25)отримаємо:

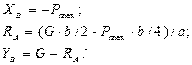
Звідки впевнюємось у вірності отримання числових значень для , 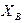та .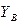

З наведених прикладів можна зробити висновок, що розв’язання задачі можна проводити за допомогою різних підходів. Тобто можна розглядати рівновагу окремих складових конструкції або рівновагу однієї частини конструкції і всієї конструкції.

Дата добавления: 2015-06-04