Приклад виконання завдання. На рис. 8.6 задана плоска фігура з розмірами в сантиметрах :a=4, b = 4, c = 6, d = 5, m = 3, n = 2, 5

На рис. 8.6 задана плоска фігура з розмірами в сантиметрах:a=4, b = 4, c = 6, d = 5, m = 3, n = 2, 5, h = 3, 6, l = 2, 4, з якої вирізано отвір у вигляді півкруга радіусом R = 1, а видалений контур L має форму квадратичної параболи y = A₁ x ² + A₂ x + A₃ з вершиною в точці K.

Визначити положення центра ваги заданої фігури згідно з пунктами 1 - 4, що містяться в умові завдання.

Рисунок 8.6

Розв’язання

: Розташовуємо задану фігуру в системі координат x Oy, як показано на рис. 8.7 Виділяємо в фігурі прості елементи і на кожному з них ставимо його номер: 1 - параболічний контур, 2 і 3 - прямокутники, 4 - трикутник, 5 - півкруг.

Рисунок 8.7

Визначаємо аналітичний вигляд параболи контуру L, який покажемо на рис. 8.8.

Рисунок 8.8

Положення крайніх точок параболи визначається розмірами:

OK = l, ON = h.

Знайдемо коефіцієнти A₁, A₂ i A₃ для параболи загального вигляду

y = A₁ x² + A₂ x + A₃. (8.1)

Для параболи (8.1) виконуються умови:

1) y = h при x = 0,
2) y = 0 при x = l,
3) dx / dy = 0 при x = l.

Звідки отримуємо систему рівнянь

h = A₁ 0 + A₂ 0 + A₃,
0 = A₁ l ² + A₂ l + A₃,
0 = 2 A₁ l + A₂ .

Яка дає розв’язки: A₁ = h / l ², A₂ = - 2 h / l, A₃ = h.

Тоді контур L має такий аналітичний вигляд

y = h x ² / l ² - 2 h x / l + h = h (x / l - 1)². (8.2)

Знайдемо площу і координати центра ваги фігури, що обмежена координатними осями і контуром L. Площа фігури визначиться інтегралом

. (8.3)

Центр ваги фігури знаходиться в точці С₁ з координатами x ₁ i y₁, які визначаються формулами:

x ₁ = I_x / S₁, y ₁ = I _y / S₁ , (8.4)

де інтеграли I_x i I_y рівні:

,

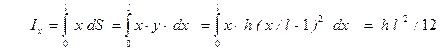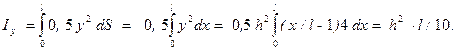
Тоді x ₁ = I_x / S ₁ = l / 4, y ₁ = I_y / S ₁ = 0, 3 h. (8.5)

Визначаємо площі і координати центра ваги прямокутників під номерами 2 і 3

S₂ = (l + m)·(a + h), (8.6)

x ₂ = (l + m) / 2,

y ₂ = (a + h) / 2.

S ₃ = n· d,

x ₃ = l + m + n / 2, (8.7)

y₃ = a + h - d / 2.

Визначаємо площу і координати центра ваги трикутника 4

S₄ = 0, 5·d·(b + c - l - m - n),

x ₄ = l + m + n + (b + c - l - m - n) / 3, (8.8)

y ₄ = a + h - d / 3.

Визначаємо площу і координати центра ваги півкруга 5

S₅ = 0, 5·p×R², (8.9)

x ₅ = b - O ₅ C ₅.

Величину відрізка О₅ С ₅, див. рис. 8.7, знаходимо як центр ваги півкруга, що є сектором з центральним кутом рівним p

O ₅ C ₅ = 4 R / (3 p), (8.10)

y ₅ = a + h - h = a.

Координати центра ваги заданої фігури знайдемо за формулами:

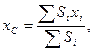
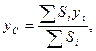(8.11)

– де вилучені площі S ₁ i S ₅ ставимо з від’ємним знаком.

В формули (8.2), (8.3), (8.5)–(8.11) підставляємо дані задачі і знаходимо координати центра ваги пластини.

Площа S ₁ і координати центра X₁,Y₁ фігури 1

,

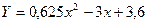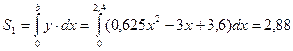см²,

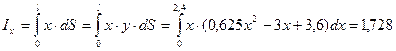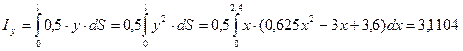см³,

см³,

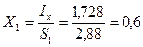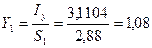см,

см.

Площі і координати центра ваги прямокутників під номерами 2 і 3

S₂ =(l+m)·(a+h)=(2,4+3)·(4+ 3, 6) = 41, 04 см ²,

x ₂ = (l + m) / 2 = (2, 4 + 3) / 2 = 2, 7 см,

y ₂ = (a + h) / 2 = (4 + 3, 6) / 2 = 3, 8 см,

S ₃ = n d = 2, 5 5 = 12, 5 см ²,

x ₃ = l + m + n / 2 = 2, 4 + 3 + 2, 5 / 2 = 6, 65 см,

y₃ = a + h - d / 2 = 4 + 3, 6 - 5 / 2 = 5, 1 см.

Площу і координати центра ваги трикутника 4

S₄ = 0,5·d(b+c-l-m-n)=0,5·5(4+6-2,4-3-2,5)=5,25 см ²,

x ₄ = l+m+n+(b+c-l-m-n)/3=2,4+3+2,5+(4+6-2,4-3-2,5)/3=8,6 см,

y ₄ = a + h - d / 3 = 4+3,6-5/3 =5, 93 см.

Площу і координати центра ваги півкруга 5

S₅ = 0,5·p R² = 0,5·3,14·1=1,57 см ²,

x ₅ = b - O ₅ C ₅.

O ₅ C ₅ = 4 R / (3 p) = 4 1 / (3 3, 14) = 0, 42 см,

x ₅ = b - O ₅ C ₅ = 4 - 0, 42 = 3, 58 см,

y ₅ = a + h - h = a = 4 см.

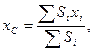
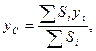
x _C = (-2,88·0,6+41,04·2,7+12,5·6,65+5,25·8,6 -1,57·3,58) /(-2,88+

+ 41,04+12,5+5,25-1,57)=231,73/54,34=4,26 см,

y _C = (-2,88·1,08+41,04·3,8+12,5·5,1+5,25·5,93-1,57·4)/54,34=

= 241, 4441 / 54, 34 = 4, 44 см.

Для обчислень контуру L і координат центра ваги заданої фігури за формулами (8.2), (8.3), (8.5) -(8.11) можна використати ПЕОМ. Для цього необхідно скласти програму. Приводимо приклад програми під назвою “CENTR” на мові “BASIC ” і результати розрахунків.

10 REM “ CENTR “

20 PI=3.14

30 A=4

40 B=4

50 C=6

60 D=5

70 M=3

80 N=2.5

90 H=3.6

100 LPRINT “ CONTUR “

110 L=2.4

120 FOR X=0 TO L STEP.3

130 Y=H*(X/L-1)^2

140 LPRINT “X=”X, “Y=”Y

150 NEXT X

160 S1=H*L/3

170 S2=(L+M)*(A+:

180 S3=N*D

190 S4=D*(B+C-L-M-N)/2

200 S5=PI*R^2/2

210 X1=L/4

220 X2=(L+M)/2

230 X3=L+M+N/2

240 X4=L+M+N+(B+C-L-M-N)/3

250 OG=4*R/(3*PI)

260 X5=B-OC

270 Y1=. 3*H

280 Y2=(A+H)/2

290 Y3=A+H-D/2

300 Y4=A+H-D/3

310 Y5=A

320 SX=-S1*X1+S2*X2+S3*X3+S4*X4-S5*X5

330 SY=-S1*Y1+S2*Y2+S3*Y3+S4*Y4-S5*Y5

340 S=-S1+S2+S3+S4-S5

350 XC=SX/S

360 YC=SY/S

370 LPRINT “--------------------------------------------------------“

380 LPRINT “XC=”XC, “YC=”YC

390 LPRINT “--------------------------------------------------------“

Дата добавления: 2015-06-04