Диссипация акустической энергии, обусловленная вязкостью и теплопроводностью среды

Тогда

Волновое уравнение для твёрдых тел

.

Откуда

Изучение динамики упругих волн в твердых телах начнем с продольных волн в стержнях. Будем описывать движение стержня при помощи неподвижной системы координат, ось X которой параллельна длине стержня (предполагается, что стержень не изгибается, а поперечное сечение его остается постоянным).

Применим 2-ой закон Ньютона к движению куска стержня, заключенного между двумя плоскостями с координатами x и 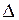x+ x.

Масса этого куска равна

m = r₀S₀ Dx,

где r₀ и S₀ – соответственно плотность и поперечное сечение стержня в отсутствии деформации (стержень считаем однородным по плотности).

Пусть x - смещение центра масс рассматриваемого куска, а s(x) и s(x+Dx) – механические напряжения (т.е. силы растяжения, приходящиеся на единицу площади поперечного сечения стержня).

.

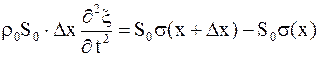Слева стоит произведение массы куска на ускорение его центра масс, справа – результирующая внешних сил, действующих на кусок. Разделим обе части уравнения на S₀×Dx:

Перейдя к пределу при Dx®0, получим

.

Растяжение куска приводит к его удлинению, т.е. к деформации. Средней продольной деформацией называют отношение удлинения Dx_xx к первоначальной длине Dx:

.

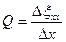Продольной деформацией в данной точке называется предел, к которому стремится это отношение при Dx®0, т.е.

.

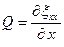Связь между напряжением и деформацией в линейном приближении описывается законом Гука

s=EQ,

где E – константа, характеризующая материал. Её называют модулем упругости (модулем Юнга).

Подставляя получим:

.

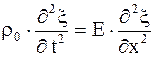Поделив обе части этого равенства на r₀, находим волновое уравнение

.

Скорость распространения упругих волн в стержне:

.

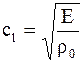Смещение частиц распространяется по стержню в виде волн:

.

Колебательную скорость частиц 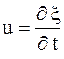, деформацию S и напряжение s получим, дифференцируя выражения по t и по x:

;

;

.

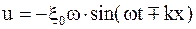Таким образом, смещение, колебательная скорость, деформация и напряжение распространяются в стержне в виде волн с одной и той же скоростью.

В твердых телах могут распространяться звуковые волны нескольких типов (мод). В безграничном изотропном твердом теле возможны продольные волны того же типа, что и в жидкости или газе и поперечные (сдвиговые волны). В твердых телах ограниченных размеров возможны волны и других мод (поверхностные, изгибные). Возможность распространения в веществе волн того или иного типа непосредственно связана с существованием определенного типа упругости (модуля упругости).

Если нижнюю грань куба зафиксировать, то, чтобы деформировать его в направлении оси x (т.е. сместить верхнюю грань на Dx_xy) необходимо к его верхней грани приложить тангенциальную силу (напряжение s_xy) (рисунок 1).

В пределах упругой деформации выполняется закон Гука:

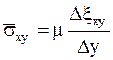
или при Dy®0:

.

Коэффициент m представляет собой модуль сдвига. Для жидкостей и газов m = 0, отсюда следует невозможность распространенения в этих средах поперечных звуковых волн.

Скорость распространения сдвиговых волн, как известно [ ], вычисляется по формуле

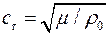. (19)

Модули Е и m для твердых тел численно отличаются друг от друга, причем Е > m, поэтому скорость распространения продольной волны больше скорости распространения сдвиговой волны. Если на одном конце стержня одновременно возбуждаются импульсы продольной и сдвиговой волн, то приходят они к другому концу стержня в различные моменты времени.

В ограниченных твёрдых телах могут распространяться также волны других типов. Из них основное значение имеют: поверхностные волны (волны Рэлея), нормальные волны в слоях (волны Лэмба), изгибные волны.

Поверхностные волны – упругие волны, распространяющиеся вдоль поверхности твёрдого тела или вдоль границы твердого с другими средами и затухающие при удалении от границ. Физическое объяснение природы поверхностных волн состоит в том, что тонкий приповерхностный слой твёрдого тела имеет модули упругости, отличающиеся от модулей упругости внутренних участков. Молекулы, находящиеся на поверхности кристаллической решетки и внутри её испытывают различное силовое воздействие со стороны ближайших соседей.

Поверхностные волны бывают двух классов: с вертикальной поляризацией, у которых частицы колеблются в плоскости, перпендикулярной к граничной поверхности, и с горизонтальной поляризацией, у которых вектор смещения частиц среды параллелен граничной поверхности.

Волны с вертикальной поляризацией называются волнами Рэлея. Они распространяются вдоль границы твёрдого тела. Энергия их локализована в приповерхностном слое толщиной от λ до 2λ. Частицы в волне движутся по эллипсам, большая полуось которых перпендикулярна к границе, а малая – параллельна направлению распространению волны. Фазовая скорость Рэлея c_R ≈ 0,9c_τ, где c_τ – фазовая скорость плоской поперечной волны.

В слоях-листах, стенках труб возбуждаются нормальные моды, их называют волны Лэмба. Волны Лэмба имеют волновидный механизм распространения. Т.е. распространяются в виде нормальных волн, образующихся в результате последовательных отражений от стенок. Скорость распространения этих волн зависит от толщины слоя и частоты.

Дата добавления: 2015-06-25