Скорость звука в системе абсолютно-твердые наночастицы в жидкой сжимаемой матрице. Аддитивная модель упругости микро- и нано- дисперсных систем

Распространение звука в микро- и нанодисперсной системе

Для получения функциональной зависимости скорости распространения звуковых волн в дисперсной среде с твердыми наночастицами дисперсной фазы (для определенности – в магнитной жидкости (МЖ)) от объемной концентрации частиц j используется известная для дисперсных сред «аддитивная» модель формирования упругости [ ].

Вывод расчетной формулы проведем предполагая, что теплообмен между компонентами гипотетической дисперсной системы отсутствует, найдем выражение для с_SS, а затем, учитывая межфазный («внутренний») теплообмен в МЖ, получим выражение для расчета с_ST.

Будем полагать, что плотности стабилизатора и жидкости-носителя приблизительно равны друг другу, поэтому воспользуемся соотношением: r=r₁(1–j)+r₂j.

Малость линейных размеров частиц дисперсной фазы по сравнению с длиной ультразвуковых волн позволяет применить к МЖ некоторые выводы механики сплошных сред и, в частности, воспользоваться формулой для скорости звука:

c=(rb_S)^-0,5, (3.1)

где r – плотность жидкости; b_S – ее адиабатная сжимаемость.

Объем МЖ состоит из объемов жидкости-носителя V₁, твердой фазы V₂ и стабилизатора V_α. Для достижения наилучшей устойчивости системы концентрация стабилизатора должна иметь оптимальное значение. Пусть величина α≡V_α/V₂ удовлетворяет этому требованию и остается постоянной для некоторого класса МЖ.

При квазистатическом возрастании внешнего давления на Δр произойдет изменение объема системы на ΔV, причем ΔV=-b_ТV×Δр, где b_Т – изотермическая сжимаемость системы.

Приращение объема системы должно быть равно сумме приращений объемов каждого компонента:

ΔV=ΔV₁+ΔV₂+ΔV_a,

где ΔV₁ , ΔV₂ , ΔV_α – приращение объема дисперсной среды, жидкости-носителя и стабилизатора.

На основании этого найдем:

b_Т=(1–j–aj)b_Т1+ajb_Тα+jb_Т2, (3.2)

где b_Т1, b_Тα, b_Т2 – изотермические сжимаемости дисперсионной среды, стабилизатора и твердой фазы; j≡V₂/V – объемная концентрация твердой фазы.

Учитывая относительно малую сжимаемость твердых тел, примем b_Т2=0. В отношении параметров b_Тa и b_Т1 сделаны два различных допущения: b_Тa<<b_Т1 и b_Тa≈b_{Т1 .} Первый случай реализуется при наличии достаточно жесткой связи молекул стабилизатора с поверхностью частиц, а второй – при отсутствии такой связи. Было бы более правильным считать b_Тa=g΄b_Т1, тогда выражение (3.2) принимает следующий вид:

β_Т=[1–j–(1–g΄)aj]b_Т1. (3.3)

При быстропеременных процессах изотермические сжимаемости b_Т1, b_Т2 и b_Тa переходят в адиабатные – b_S1, b_S2 и b_Sa, имеющие при отсутствии диссипативных процессов действительное значение.

Адиабатная сжимаемость дисперсной системы равна сумме удельных сжимаемостей компонент, входящих в систему.

Если пренебречь взаимным влиянием компонентов, то адиабатная сжимаемость системы представляет сумму удельных адиабатных сжимаемостей:

b_S=[1–j–(1–g΄)aj] b_S1. (3.4)

При достижении удовлетворительного согласия с опытом, найденное значение параметра γ΄ может дать представление об относительной сжимаемости компонентов реальной МЖ.

Подстановка (3.4) в (3.1) позволяет записать скорость распространения звука в МЖ в виде

с_SS=с₁r₁^0,5{r [1–j–(1–g΄)aj]}^-0,5, (3.5)

где с₁≡(r₁b_S1)^-0,5 – скорость звука в чистой дисперсионной среде.

Концентрация твердой фазы в МЖ рассчитывается по формуле:

j=(r–r₁)/(r₂–r₁). (3.6)

Поэтому

с_SS=с₁{(1–j+jr₂/r₁)[1–j–(1–g΄)aj]}^-0,5. (3.7)

Заменяя в соотношении (3.5) j по формуле (3.6), получим

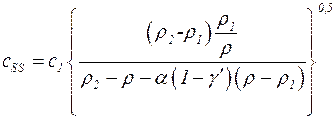(3.8)

Среду с малыми неоднородностями и расстояниями между ними в сравнении с длиной волны принято называть микронеоднородной [93, 94]. МЖ представляет уникальный пример микронеоднородной среды [9]. Диспергированные в жидкости-носителе магнитные частицы имеют столь малые размеры, что данное условие выполняется во всем ультразвуковом диапазоне.

При прохождении звуковой волны происходят периодические сжатия и растяжения компонент МЖ, причем «макроскопически» этот процесс, как и для большинства однородных жидкостей, протекает адиабатно. Однако изменение температуры компонент системы, обусловленное переменным звуковым давлением, различно. Благодаря малости и относительно высокой теплопроводности ФЧ их температура будет успевать выравниваться с температурой жидкости-носителя, поэтому процесс будет «микроскопически» изотермичен. Критическая частота, ниже которой простирается область частот, соответствующая данному процессу, находится из выражения [94]:

,

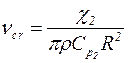где c₂ и С_р2 – теплопроводность и удельная теплоемкость при постоянном давлении твердых частиц; R – их радиус; r – плотность МЖ.

Для малоконцентрированной МЖ 1-го типа n_cr ≈10¹¹ Гц. В обычных эмульсиях процесс распространения звука может быть «микроскопически» и адиабатным, и изотермическим [94]. В дальнейшем будем обозначать скорость звука в случае адиабатного «макроскопически» и адиабатного «микроскопически» процесса с_SS, а в случае адиабатно-изотермического процесса – с_ST.

Механизм выравнивания температуры между компонентами МЖ оказывает влияние на величину адиабатной сжимаемости и скорости распространения звука. Для разбавленных дисперсных систем при выполнении условия n<<n_cr имеет место выражение, полученное М.А. Исаковичем [94]:

. (3.9)

где ρ — плотность МЖ; С_р1 и С_р2 – удельные теплоемкости; q₁ и q₂ – коэффициенты теплового расширения дисперсионной среды и дисперсной фазы.

При j <<1 приращение скорости звука в МЖ может быть записано в виде суммы:

Δс_ST=Δс_r+Δс_b+Δс_Т,

в которой отдельные слагаемые представляют вклад каждого из перечисленных факторов:

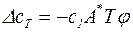; ; , (3.10)

где .

Численное значение А* можно найти из выражения А*Тj= 0,026, полученного для МЖ с параметрами: r =1230 кг/м³, с₁ =1200 м/с, С_р1 =2 кДж/(кг·К), С_р2 =0,655 кДж/(кг·К), q₁ =9,5·10^-4 К^-1, q₂ =11,4·10^-6 К^-1, r₂ =5,21·10³ кг/м³, j =0,1, Т =300 К.

Из формулы (3.10) для j =0,05 следует Δс_r =-184 м/с, Δс_b =75 м/с и Δс_Т =-17 м/с.

Агрегаты и кластеры в МЖ будут иметь термодинамические параметры, несколько отличные от параметров окружающей среды, что могло бы отразиться на упругих свойствах нанодисперсной системы.

В дисперсных системах может наблюдаться и гравитационная диффузия (бародиффузия). Отношение магнитной силы, действующей на частицу, к гравитационной не зависит от размеров частиц: . При 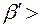1 магнитная сила преобладает над гравитационной, при 1 – гравитационная над магнитной. Характер магнитного воздействия радикально отличается от воздействия гравитации благодаря тому, что с его помощью можно получить переменный по интенсивности и направлению массоперенос магнитного материала в конечном объеме, например в акустической кювете, что в свою очередь позволяет создать требуемую геометрию распределения концентрации и скорости звука по объему, управлять сечением и направленностью звуковых пучков.

Дата добавления: 2015-06-25