Коэффициенты отражения и прохождения звуковых волн

Отражение и прохождение звука через границу раздела двух сред

Акустические измерения широко используются в научных исследованиях и различных технологических процессах. Измерения такого рода сводятся главным образом к измерению скорости распространения и коэффициента поглощения акустических волн в исследуемых средах. Они применяются в молекулярной акустике [1], теоретическую основу которой составляет релаксационная теория. На основе данных о дисперсии звука и об особенностях его поглощения получают сведения о различных молекулярных процессах в газах, жидкостях, полимерах. Результаты измерений в диапазоне частот от 0,1 МГц до 10 ГГц позволяют выяснить особенности молекулярной структуры вещества, определить энергию взаимодействия молекул, проверить гипотезы о тех или иных моделях молекулярной структуры вещества. Ультразвуковые методы, основанные на измерениях скорости и затухания звука, используются также в технике для определения свойств и состава веществ. Ультраакустические измерения позволяют выявить дисперсный состав гетерогенных сред, устойчивость системы, осуществлять контроль различных физических и химических процессов, протекающих при получении полимеров, в том числе синтетического каучука, в пищевой промышленности, в производстве минеральных удобрений, в нефтедобывающей промышленности и т.п. В реальной среде, характеризуемой определенной сдвиговой и объемной вязкостью, теплопроводностью, различного рода включениями, амплитуда бегущей волны убывает с расстоянием, т.е. упругая энергия рассеивается (диссипирует), превращаясь в конечном итоге в тепловую энергию [1]. Если интенсивность плоской звуковой волны на расстоянии x от источника равна. То вследствие диссипации упругой энергии в плоскопараллельном слое среды толщиной dx происходит убыль интенсивности dI на величину

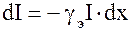, (17.1)

где - энергетический коэффициент поглощения.

Разделив переменные в уравнении (17.1) имеем

.

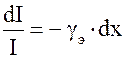Интегрируя это уравнение в пределах от источника (x = 0, ) до произвольной точки x, получим закон уменьшения интенсивности звука с расстоянием

. (17.2)

Согласно (3.12) , поэтому после извлечения из обеих частей выражения (17.2) квадратного корня, получим

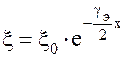
или

, (17.3)

где - коэффициент поглощения звуковой волны.

Из (17.3) следует, что в результате диссипации звуковой энергии амплитуда смещения частиц убывает с расстоянием по экспоненциальному закону, причем энергетический коэффициент поглощения равен удвоенному амплитудному коэффициенту поглощения.

Рассмотрим вклад в диссипацию звуковой энергии механизмов, связанных с вязкостью и теплопроводимостью сред.

Выражение для энергии dI, которая превращается в тепло в объеме из-за действия вязких сил, выражается формулой:

. (17.8)

Сравнивая правые части (17.7) и (17.1), находим для коэффициента поглощения по энергии γ_э и по амплитуде звуковой волны α выражения:

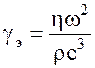; (17.9)

. (17.10)

Следует отметить, что в выражениях (17.9) и (17.10) под коэффициентом понимают эффективную вязкость. Для продольных волн

, (17.11)

где - сдвиговая вязкость;

- объемная вязкость.

Объемная вязкость определяет диссипативные силы, возникающие при всестороннем расширении или сжатии реальной среды.

Таким образом, коэффициент поглощения, обусловленный эффективной вязкостью, прямо пропорционален квадрату частоты. Однако этот вывод на практике подтверждается лишь в области относительно низких частот, что связано с релаксационными свойствами вязкости и относится к предмету изучения молекулярной акустики.

Вклад теплопроводности в поглощение звука впервые был учтен Кирхгофом в 1868 г.

Звуковые волны представляют собой адиабатный процесс. При распространении звука в фазе сжатия происходит нагревание, а в фазе разряжения – охлаждение среды. В результате теплообмена между местами с различной температурой будет происходить обмен энергией, так что процесс деформации оказывается не строго адиабатным. Теплообмен между соседними полуволнами влечет за собой уменьшение амплитуды звукового давления (возмущение плотности) и способствует превращению упругой энергии в тепловую энергию.

Поглощение звука, вызванное теплообменом, для не слишком высоких частот, пропорционально квадрату частоты

, (17.12)

где – коэффициент теплопроводности среды;

С_P и C_V - молярные теплоемкости.

Суммарный коэффициент поглощения звука имеет вид:

. (17.13)

Формула (17.13) при носит название формулы Стокса-Кирхгофа.

Полезно оценить сравнительную роль разных членов в выражении (17.13). Вопрос о роли объемной вязкости мы рассмотрим отдельно. Вклад сдвиговой вязкости и теплопроводности в поглощение оказывается различным. В случае газов вязкость и теплопроводность примерно одинаково влияют на поглощение. Для большинства жидкостей (за исключением жидких металлов) член с теплопроводностью составляет несколько процессов и его можно не учитывать. В жидких (расплавленных) металлах большая часть поглощения вызвана теплопроводностью.

ЗАДАЧИ:

1. Наночастицы, диспергированные в жидкости, при распространении в ней упругой (звуковой, ультразвуковой, гиперзвуковой) волны оказываются под воздействием переменного по знаку всестороннего давления:

.

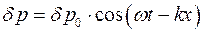Перепад давления в звуковой волне на расстоянии, равном диаметру магнитной наночастицы D:

Δp = .

Получить численное значение отношения Δp/δp₀= kD=2πνD/cпри D= 10^{-8 м, ν= 20 · 103} Гц, c= 10³ м/с. (~ 10^-6)

2. В звуковой волне в результате адиабатности процесса колебаний среды наблюдаются колебания температуры δТ:

;

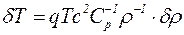где 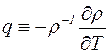– температурный коэффициент расширения;

– плотность жидкости;

с – скорость распространения звука в МЖ в отсутствие магнитного поля;

С_p – удельная теплоемкость при постоянном давлении и постоянной напряженности магнитного поля;

δρ/ρ – деформация среды.

Оценку «сверху» колебаний температуры выполним в предположении, что амплитуда деформации в звуковой волне составляет 10^-4. При таком значении амплитуды деформации в магнитной жидкости могут появляться отдельные воздушные пузырьки – предвестники ультразвуковой кавитации и другие нелинейные эффекты.

Пусть C_p= 2·10³ Дж/кг·К, c =1120 м/с, q =0,53·10^-3 К^-1, Т = 300 К, тогда δТ ≈ 10^-2 К.

9.. Пренебрегая массой элемента трубы и принимая в расчет только его упругость, получена следующая формула, связывающая с и с₀:

,

где R₁ – внешний радиус трубы, R₂ - внутренний радиус трубы, 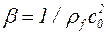- сжимаемость жидкости.

Рассчитать скорость звука в жидкости, заполняющей стеклянную трубу. Параметры стекла: модуль Юнга Е =7,26·10¹⁰ Па, плотность стекла r_t =2400 кг/м³, скорость продольных волн в стекле с =5500 м/с. Скорость звука в «неограниченной» жидкости с₀ =1200 м/с. ρ_f = 1000 м/с. Стенки трубы: R₁ =7 мм; R₂ =6мм.

3. Для оценки относительного приращения намагниченности МЖ 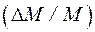за счет деформации среды в отсутствие тепловых колебаний, т.е. при q = 0, имеем:

,

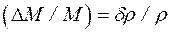где М и ρ – намагниченность и плотность среды в невозмущенном состоянии.

Пусть C_p= 2·10³ Дж/кг·К [35], c =1120 м/с [64], q =0,53·10^-3 К^-1, тогда 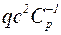=0,33.

При сделанных выше допущениях 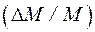≤10^-4.

С учетом тепловых колебаний в звуковой волне:

≤0,5·10^-4.

Таким образом, ультрамалые тепловые колебания, сопровождающие звуковую волну, вносят в возмущение намагниченности МЖ вклад, соизмеримый со вкладом колебаний концентрации наночастиц дисперсной фазы.

ДРУГИЕ ЗАДАЧИ ПО АКУСТИКЕ

1. Найти длину волны звука с частотой 435 Гц, распространяющегося в воздухе. Скорость звука принять равной 340 м/с. (0,78 м)

2. Человеческое ухо может воспринимать звуки с чостотой от 20 Гц до 20 кГц. Найти соответствующий диапазон длин волн. Скорость звука принять равной 340 м/с. (17мм – 17м)

3. Найти скорость распространения звука в воздухе при температурах: -20^оС; 0 ^оС; +20 ^оС.

4. Во сколько раз скорость распространения звука в воздухе летом (+20 ^оС) больше скорости звука зимой (-25 0 ^оС).

5. Зная, что средняя квадратичная скорость молекул двухатомного газа была равна 461 м/с, найти скорость распространения звука в газе при этих условиях.

6. Найти скорость распространения звука в двухатомном газе, если известно, что плотность этого газа при давлении 760 мм рт. ст.равна 1,29 кг/м³.

7. Зная, что средняя кинетическая энергия поступательного движения молекул одного киломоля азота равна 3,4 10³ кДж, найти скорость распространения звука в азоте при этих условиях. (336 м/с)

8. При образовании стоячей волны в трубе, заполненной воздухом, образовалось 5 пучностей. Какова длина трубки? Скорость звука в воздухе принять равной 340 м/с, частота звуковых колебаний 100 Гц, на торцах трубы расположены пучности.

9. Скорость звука в керосине 1330 м/с. Плотность ρ=800 кг/м³. Найти адиабатную сжимаемость керосина.

10. Найти скорость распространения звука в алюминии. Е=6,9 10¹⁰Н/м², ρ=2600 кг/м³.

11. Найти скорость распространения звука в меди Е=11,8 10¹⁰Н/м², ρ=8600 кг/м³.

12: В результате взрыва, произведенного геологами, в земной коре распространилась волна со скоростью 4,5 км/с. На какой глубине залегает порода другой плотности, если отраженная от нее волна была зафиксирована на поверхности через 20 с после взрыва?

13: Из орудия произвели выстрел под углом 26° к горизонту. Артиллерист услышал звук разрыва снаряда через 44 с после выстрела. Какова горизонтальная дальность полёта снаряда, если его начальная скорость 800 м/с?

ПРИМЕЧАНИЕ. Формулы кинетической энергии молекул газа в зависимости от числа степеней свободы

Таблица 12.1

i = 3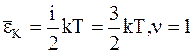
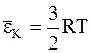
i = 5
i = 6

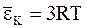
R=8,31∙10³ Дж/кмоль∙К

При падении звуковой волны на границу раздела двух сред в общем случае появляются две волны — отраженная и прошедшая (преломленная). Мы рассмотрим лишь случай нормального падения плоской монохроматической волны на плоскую границу раздела сред. Сформулируем граничные условия.

При одновременном существовании на границе трех волн (падающая, отраженная и прошедшая) должны быть выполнены условия непрерывности сплошности среды и равенство сил по обеим сторонам границы раздела.

Допустим, что две среды разделены плоскостью х = 0 так, что по обеим сторонам имеются среды со значениями плотности и скорости звука r₁c₁ и r₂c₂. На границе раздела при х = 0 смещение частиц первой и второй сред вследствие неразрывности среды равны:

. (16.14)

Поэтому равны и производные по времени:

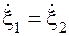; (16.15)

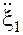= . (16.16)

Вследствие третьего закона Ньютона должны быть одинаковыми и звуковые давления

p₁ = p₂. (16.17)

Запишем уравнение движения двух сред в виде:

;

.

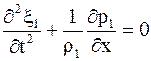Учитывая (16.16), получим:

.

Откуда

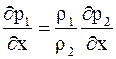. (16.18)

Таким образом, на границе раздела двух сред отношение градиентов давления равно отношению плотностей.

Расположим ось X так, чтобы ее положительное направление было противоположно направлению падающей волны. Первая среда находится в области отрицательных значений х, вторая – в области положительных (рис. 16.4).

Плоская волна в первой среде состоит из отраженной волны и падающей волны.

Воспользовавшись экспоненциальной формой представления уравнения волны, запишем для первой среды:

;

.

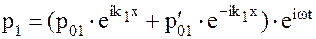Во второй среде имеется только проходящая волна

;

.

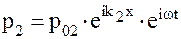На границе раздела (х = 0) имеем:

;

. (16.18^/)

Между давлением и колебательной скоростью существует соотношение:

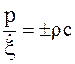, (16.18^//)

где знак "плюс" берут для волны, распространяющейся в положительном направлении оси х, а знак "минус" для волны, распространяющейся в противоположном направлении.

Используя эти соотношения, имеем:

;

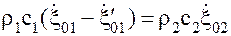. (16.19)

Поделив первое уравнение на , а второе - на получим:

; , (16.20)

где 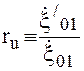коэффициент отражения волны скорости;

 - коэффициент прохождения;

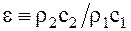-отношение волновых сопротивлений.

Решая уравнения (16.20), находим:

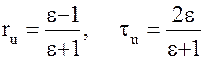. (16.21)

Исключив из (16.18^/) с учетом (16.18^//) можно получить уравнение для давления

;

.

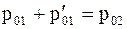Обозначив, перепишем эти уравнения в виде:

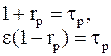. (16.22)

Решая систему уравнений (16.22) относительно и 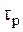, находим:

(16.23)

Так как между давлением и интенсивностью имеются соотношения

,

то коэффициент отражения и прохождения звука по интенсивности определяется по формулам:

(16.24)

Через приведенное волновое сопротивление e эти коэффициенты выражаются по формулам:

. (16.25)

Рассмотрим применение формул прохождения и отражения для крайнего случая, когда e<<1. Это практически получается, если звук проходит из твердого тела в воздух.

При распространении звука из акустически жесткой среды в мягкую (r₁с₁>>r₂с₂) коэффициент отражения волны давления имеет значение r_p» -1.

Это значит, что при прохождении волны давления из твердого тела в воздух амплитуда отраженной волны давления приблизительно равна амплитуде падающей волны, но имеет противоположный знак. Иными словами, фаза волны давления при отражении от акустически мягкой среды изменяется на p (можно сказать, что происходит потеря полуволны). Коэффициент прохождения t_p в этом случае приблизительно равен 0, то есть волна практически не проходит во вторую среду. То же самое происходит, если взять коэффициент прохождения по интенсивности:

.

Если же среды отличаются по своим волновым сопротивлениям не столь резко, то возможно наряду с отражением и частичное прохождение волны во вторую среду.

Дата добавления: 2015-06-25