Операторные методы в теории автоматического регулирования

План лекции –

1. Цели и сущность операторных методов.

2. Преобразования Лапласа для временных функций

3. Передаточная функция

Литература: [1], [2], [3].

1. Целью рассмотрения системы автоматического регулирования может быть решение одной из двух задач – задачи анализа системы или задача ее синтеза.

В первом случае исследуется система с заданными значениями параметров, и требуется определить ее свойства. Во втором случае, наоборот, задаются свойства, которыми должна обладать система, т.е. требования к ней, и необходимо создать структуру системы, удовлетворяющую этим требованиям. В самом общем виде порядок исследования САУ в обоих случаях включает математическое описание системы или математической модели. Математические модели системы представляют собой уравнения динамики, записанные в виде дифференциальных уравнений различных порядков. В общем случае дифференциальное уравнение автоматической системы имеет вид:

где все коэффициенты – величины постоянные.

С целью упрощения методов расчета САУ уравнения динамики записывают не через оригиналы функций, а в виде изображений функций (операторов), полученных с помощью прямого преобразования Лапласа. Этот метод заключается в том, что с одной стороны, изменяется форма записи дифференциальных уравнений (они становятся алгебраическими), а с другой – функция времени заменяется, или как говорят, изображается функцией комплексного аргумента . Принцип перехода от оригиналов каких-либо функций к ее изображениям не является новым и широко используется не только в теории автоматического регулирования. Например, с понятием изображения сталкиваются, когда изучают логарифмы. Так, если число 3,5 нужно возвести в степень 2,5, то находят логарифмы числа 3,5 и умножают его на 2,5. Полученный логарифм переводят в число, которое и будет ответом на поставленный вопрос. Таким образом, схема возведения числа в степень имеет вид:

число ® его изображение (логарифмы) ® действие над этим изображением (умножение, деление) ® число (оригинал) ® ответ.

Схема решения дифференциального уравнения операторным методом ничем не отличается от только что приведенной схемы для возведения в степень числа, только здесь изображаются не числа, а функции времени.

2. Соответствие между изображением F(p) и функцией времени (оригиналом) f(t) обозначается символом преобразования L (прямое преобразование) или L^-1 (обратное преобразование): F(p)=L[f(t)] или
f(t)=L^-1[F(p)].

Формально изображение F(p) находится через оригинал с помощью интегрального преобразования Лапласа:

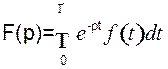
Например, найти изображение постоянной y(t)=A. Тогда в соответствии с (2), получим.

F(p)=L[A]= e^-ptf(t)dt = – 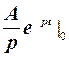= – 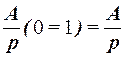(2)

Составлены таблицы прямых и обратных преобразований оригиналов в изображения и наоборот.

Таблица 1

№п/п	Оригинал f(t)	Изображение по Лапласу F(p)

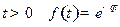
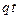
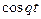
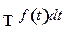
Здесь значение функции при .

Преобразование Лапласа имеет ряд важных свойств:

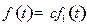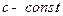а) Преобразование Лапласа является линейным. Если , где , то

.

Изображение суммы оригиналов равно сумме изображений. Если 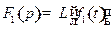и , то

.

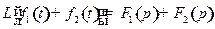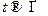б) Теорема о предельном значении. Если имеет предел при , то это предельное значение может быть найдено по формуле

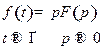(3)

Приведем пример использования операционного исчисления для решения дифференциальных уравнений.

Пример. Найти решение уравнения

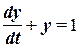при и

Находим изображения членов исходного уравнения, воспользовавшись табл.1.

,

откуда

.

Далее переходя к оригиналам, получим решение:

.

3. Операторный метод дает удобный способ анализа линейных устройств и систем с помощью их передаточных функций.

Передаточной функцией системы называется отношение выходной величины системы к входной, записанное в операторной форме при нулевых начальных условиях. Если динамика системы описывается обыкновенным дифференциальным уравнением вида:

то определив изображение по Лапласу правой и левой части уравнения при нулевых начальных условиях:

,

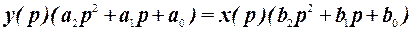получим следующую передаточную функцию системы:

(4)

Если выходной, а входной сигнал автоматической системы, то функции показывает в операторной форме, какое преобразование производит система над входным воздействием , с тем, чтобы на ее выходе получалась величина .

Дата добавления: 2015-06-25