Статистическая оценка числовых характеристик 3 страница

4. Контрольная работа состоит из 6 задач, причём для успешного её выполнения необходимо решить любые четыре задачи. Если студент будет решать в течение отведённого времени лишь 4 задачи, то вероятность правильного решения любой из них равна 0.8. Если он попробует решить 5 задач, то вероятность правильного решения любой из них равна 0,7, а если он возьмётся за решение всех шести задач, то эта вероятность снизится до 0,6. Какой тактики должен придерживаться студент, чтобы иметь наибольшие шансы успешно выполнить работу?

5. Предполагается, что вероятность выздоровления больного в результате применения нового способа лечения равна 0,8. Сколько вылечившихся из 100 больных можно ожидать с вероятностью 0,75?

6. Из колоды в 36 карт извлекают три. Найти распределение вероятности числа тузов. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.

7. Случайная величина Х задана функцией распределения:

F(x)=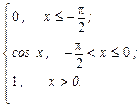

Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины. Вычислить вероятность того, что случайная величина Х примет значение в интервале .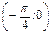

8. Известны математическое ожидание m и среднее квадратическое отклонение s нормально распределённой случайной величины Х. Найти вероятность попадания этой величины в заданный интервал (a, b). Изобразить на графике функции плотности найденную вероятность.

m=5, s=1, a=1, b=12.

1. Шесть хоккеистов сложили свои клюшки в одно место. После перерыва они разобрали клюшки случайным образом. Сколько существует вариантов, при которых только трое хоккеистов взяли свои клюшки?

2. В экзаменационные билеты включено по два теоретических вопроса и одной задаче. Всего составлено 28 билетов, содержащих разные вопросы и задачи. Студент подготовил только 50 теоретических вопросов и сможет решить задачи к 22 билетам. Какова вероятность того, что вынув наудачу один билет, студент ответит на все вопросы?

3. По самолёту производится три выстрела. Вероятность попадания при первом выстреле равна 0,5, при втором – 0,6, при третьем – 0,8. При одном попадании самолёт сбивается с вероятностью 0,3, при двух - с вероятностью 0,6 и при трёх сбивается наверняка. Какова вероятность сбить самолёт?

4. Вероятность попадания в мишень одним выстрелом равна 1/8. Какова вероятность того, что из 12 выстрелов не будет ни одного попадания?

5. Прядильщица обслуживает 1000 веретён. Вероятность обрыва нити на одном веретене в течение одной минуты равна 0,004. Какова вероятность того, что в течение одной минуты обрыв произойдёт на пяти веретенах?

6. Производится стрельба по цели до первого попадания. Вероятность попадания при каждом выстреле равна 0,25. Найдите математическое ожидание и дисперсию случайного числа произведённых выстрелов.

7. Случайная величина Х задана функцией распределения:

F(x)=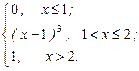

Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины. Вычислить вероятность того, что случайная величина Х примет значение в интервале (1,5; 3,5).

8. Известны математическое ожидание m и среднее квадратическое отклонение s нормально распределённой случайной величины Х. Найти вероятность попадания этой величины в заданный интервал (a, b). Изобразить на графике функции плотности найденную вероятность.

m=1, s=1, a=0, b=3.

1. В кафе позвонили 4 человека и заказали по одной пицце. Каждая пицца должна была иметь свою особенность. Разносчик перепутал их и доставил не так, как они были заказаны. Сколько имеется вариантов распределения пицц, в которых только одному заказчику попала своя пицца?

2. Из колоды в 36 карт наугад одну за другой вынимают две карты. Найти вероятность того, что:

а) вынуты два валета;

б) вынут валет и дама.

3. В продажу поступают телевизоры трёх заводов. Продукция первого завода содержит 20% телевизоров со скрытым дефектом, второго – 10% и третьего – 5%. Определить вероятность приобретения исправленного телевизора, если в магазин поступили 30 телевизоров с первого завода, 20 –со второго и 50 – с третьего.

4. По цели производится шесть независимых выстрелов. Вероятность попадания при каждом выстреле р=0,75. Вычислите:

а) вероятность ровно пяти попаданий;

б) вероятность не менее пяти попаданий;

в) вероятность менее пяти попаданий.

5. Вероятность выпуска бракованного сверла равна 0,015. Сверла укладывают в коробки по 100 штук. Найти вероятность того, что в коробке, выбранной наудачу, не окажется ни одного бракованного сверла.

6. Рассматривается работа трёх независимо работающих технических устройств (ТУ). Вероятность нормальной работы первого ТУ равна 0.2, второго – 0.4, третьего – 0,5. Постройте закон распределения числа работающих ТУ. Найдите .

7. Случайная величина Х задана функцией распределения:

F(x)=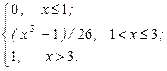

Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины. Вычислить вероятность того, что случайная величина Х примет значение в интервале (1,5; 3,2).

8. Известны математическое ожидание m и среднее квадратическое отклонение s нормально распределённой случайной величины Х. Найти вероятность попадания этой величины в заданный интервал (a, b). Изобразить на графике функции плотности найденную вероятность.

m=1.5, s=1, a=0.5, b=2.5.
Приложение Н

Семестровая работа по предмету «математическая статистика»

Наблюдаемые значения случайных величин Х, У определяются по правилу: X = Z_i, У = Z_j, где индексы i, j определяются номером варианта с помощью табл. 1. Например, для варианта № 10 выбираем клетку в таблице 1 с цифрой 10. Соответствующие индексы i =1, j =5 – номера столбца и строки, проходящей через рассматриваемую клетку.

Таблица Н. 1 – Выбор варианта

j	i

Значения Z_i, Z_j приведены в таблице Н. 2. Необходимо с помощью пакета программ “STATISTICA”:

1. Построить облако данных на плоскости Х,У и выполнить графически группировку наблюдений величин.

2. Составить корреляционную таблицу и вычислить выборочные средние, дисперсии, асимметрии и эксцессы, коэффициент корреляции случайных величин Х, У с помощью метода произведений и пакета программ “STATISTICA”.

3. Построить гистограммы относительных частот, кумуляты и проверить гипотезу о нормальном распределении величин Х, У с уровнем значимости 0,05.

4. с помощью метода произведений и пакета программ “STATISTICA” найти выборочное уравнение прямой линии регрессии У на Х, изобразить линию регрессии на облаке данных и проверить гипотезу об отсутствии корреляционной связи между величинами Х, У.

5. Найти выборочное уравнение связи х = ay + bZ ₇ + cZ ₈ + dZ ₉ + + e, сравнить эмпирические и расчетные значения функции х. Определить, какие независимые переменные этой связи являются значимыми, и найти выборочное уравнение только с этими переменными.

Таблица Н. 2. Статистические данные

Z 1	Z 2	Z 3	Z 4	Z 5	Z 6	Z 7	Z 8	Z 9
24,82	16,15	41,79	21,6	36,32	21,47	44,91	18,67	20,28
16,6	33,42	45,39	17,89	42,13	29,93	45,48	32,85	18,76
28,05	14,47	42,53	18,41	34,8	24,23	55,06	35,16	16,17
19,31	12,83	37,65	17,73	35,67	20,52	53,39	33,62	18,78
27,25	23,05	27,59	17,49	36,59	15,82	46,96	23,79	16,32
19,56	7,28	34,82	15,57	30,89	18,9	27,11	18,96	18,37
20,45	33,94	30,84	18,9	36,21	24,13	29,24	24,11	16,48
15,46	15,01	30,58	18,43	36,42	18,12	31,25	19,41	17,57
20,77	20,1	37,31	23,57	37,59	25,67	35,26	27,39	13,21
21,95	18,55	29,47	11,31	34,48	31,75	25,3	22,14	16,9
25,6	17,68	53,67	21,56	40,37	25,47	32,7	29,71	17,92
28,27	21,2	54,85	12,57	34,19	24,14	57,62	32,24	10,63
19,7	28,69	35,75	14,44	38,61	19,85	18,02	33,67	11,56
18,09	8,21	30,48	13,31	35,6	18,53	19,46	23,43	15,32
13,28	14,92	28,71	12,07	33,51	16,41	41,89	32,51	13,84
33,17	17,92	60,19	21,54	20,76	29,95	50,27	21,34	42,73
30,93	28,55	48,22	22,04	16,7	38,45	61,9	22,24	26,07
27,66	26,99	52,96	18,42	27,65	31,41	32,38	20,02	11,45
28,21	30,93	39,99	20,66	31,83	29,54	31,64	16,46	29,24
34,15	23,68	70,26	18,08	32,19	26,01	50,78	27,29	23,93
26,79	25,77	61,73	18,67	19,63	34,61	40,43	18,31	37,17
26,31	12,04	41,59	16,89	21,29	28,64	46,61	18,04	30,55
25,44	14,29	47,74	23,42	24,96	22,32	23,01	22,9	21,99
32,01	18,23	30,94	20,42	32,05	30,07	43,17	16,82	39,68
31,43	25,86	69,48	15,7	20,5	32,4	37,49	20,21	36,66
32,54	29,25	81,55	23,96	31,21	37,03	55,72	29,16	51,35
31,25	27,31	69,16	20,71	26,04	35,18	40,14	20,51	31,58
34,97	24,43	67,96	25,58	28,77	28,78	49,12	24,9	34,92
30,12	23,96	50,6	28,68	32,08	28,71	36,74	24,39	21,89
38,48	28,3	71,92	25,58	23,08	24,67	32,09	25,79	18,76
33,34	26,62	66,99	27,3	26,64	21,32	23,93	17,78	39,84
28,64	32,03	55,27	31,93	31,08	34,03	36,02	23,66	29,23
32,64	25,54	53,74	19,43	35,65	23,74	17,85	23,12	24,36
22,87	20,18	26,67	18,17	22,94	21,46	36,29	15,35	21,16
28,94	30,72	62,33	20,67	38,82	31,17	41,5		37,62

Продолжение таблицы Н. 2

Z 1	Z 2	Z 3	Z 4	Z 5	Z 6	Z 7	Z 8	Z 9
34,9	22,46	48,67	29,56	32,27	29,95	38,19	19,45	25,11
32,2	30,77	71,91	20,54	33,65	41,91	28,62	22,11	28,74
34,54	28,88	35,67	21,38	31,79	30,66	66,97	23,48	30,04
22,28	16,34	49,72	16,14	21,82	27,1	41,56	17,92	22,99
40,06	17,01	72,94	30,66	26,52	30,25	67,33	17,06	34,48
24,72	29,77	46,69	22,69	32,67	28,14	48,01	20,8	18,45
27,85	18,64	55,97	11,28	26,75	20,05	26,91	18,61	26,39
34,67	18,71	62,15	16,68	32,01	29,24	43,37	18,34	36,38
26,77	24,29	52,72	17,18	28,25	36,81	45,36	21,89	23,76
37,41	37,33	83,81	23,92	38,12	35,28	57,47	29,01	48,8
30,77	19,9	29,83	20,44	34,46	25,73	41,51	21,84	25,04
32,21	24,81	49,88	16,81	29,89	23,83	15,5	21,81	25,31
26,9	19,04	46,02		13,28	22,72	24,51	18,65	27,06
28,97	23,97	44,86	22,23	33,16	32,64	31,23	17,81	24,87
29,96	15,46	67,43	20,06	33,72		35,33	26,04	21,17
28,03	15,21	29,18	15,84	18,91	30,78	29,35	18,06	30,22
32,5	24,32	36,14		29,8	35,65	34,94	21,59	40,48
28,67	16,6	20,35	24,02	25,86	21,13	31,62	17,93	14,81
32,97	25,84	50,7	28,05	31,86	36,09	58,02	22,67	27,98
29,1	16,56	54,01	15,49	20,18	31,13	27,67	18,71	40,35
35,62	20,28	55,15	22,85	30,38	32,06	22,49	29,69	26,72
26,97	26,55	40,13	9,2	28,38	32,69	32,91	22,99	23,89
34,78	26,83	27,58	24,3	28,53	31,84	41,19	21,56	16,61
27,97		59,34	18,31	27,3	20,07	39,56	25,4	10,09
	18,12	18,18	16,85	33,01	25,2	38,23	21,7	11,27
28,63	28,09	60,99	22,02	25,93	26,24	57,79	23,55	29,95
27,05	27,97	42,98	20,78	23,65	30,97	58,97	18,54	40,03
32,19	22,13	76,33	25,88	36,01	23,95	63,53	26,14	19,83
31,17	13,66	72,15	16,97	33,15	26,95	38,74	21,36	39,13
25,57	14,96	27,73	20,98	34,25	34,9	44,15	22,03	14,25
17,93	16,92	24,07	25,8	30,84	27,05	41,28	16,68	31,64
27,73	21,48	66,77	25,5	34,66	32,19	39,54	18,99	37,07
35,05	23,22	52,39	32,85	43,38	34,19	35,6	18,42	39,75
27,38	25,18	70,58	25,45	27,96	36,38	44,08	24,06	12,51
31,7	26,76	59,88	22,09	25,66	28,58	30,05	22,82	40,04

Продолжение таблицы Н. 2

Z 1	Z 2	Z 3	Z 4	Z 5	Z 6	Z 7	Z 8	Z 9
28,43	19,59	54,44	11,25	23,95	21,62	33,71	21,27	11,4
30,85	18,87	41,31	25,3	26,81	29,8	45,37	19,56	30,62
32,22	23,13	36,84	21,44	27,39	23,24	46,92	20,84	27,34
33,96	21,92	66,23	17,12	30,32	28,84	59,08	23,47	18,04
30,81	21,05	61,97	20,03	34,65	30,18	45,67	15,05	29,29
31,35	22,66	52,32	15,05	29,67	27,5	39,26	19,69	29,2
32,32	21,79	63,24	22,79	35,97	40,36	33,36	20,69	30,6
26,98	23,15	34,08	28,46	36,78	33,25	36,47	15,03	16,03
33,02	16,36	47,65	19,37	27,02	20,33	39,66	17,99	23,3
35,71	22,24	80,98	17,11	35,56	35,59	47,63	24,77	28,02
31,76	15,92	69,93	20,6	19,8	25,38	42,51	23,7	17,99
31,27	23,26	47,82	22,7	18,15	19,52	18,32	16,84	29,12
27,43	30,1	59,33	26,86	29,6	26,49	23,73	30,04	37,86
24,73	18,56	29,82	12,85	22,93	32,49	38,32	21,6	11,91
33,76	14,85	38,82	21,94	32,35	25,25	45,85	20,02	22,4
29,59	30,56	56,89	28,96	29,3	30,33	38,59	26,82	40,43
29,46	26,6	80,41	15,53	35,22	30,43	28,75	21,87	17,02
39,89	34,55	71,77	16,44	39,42	37,59	41,04	23,67	34,89
27,75	26,36	46,16	18,02	28,83	22,73	20,05	21,76	32,24
26,8	20,52	38,9	24,66	26,82	36,21	47,95	21,19	10,97
31,5	27,8	70,25	24,49	36,12	35,47	29,1	20,04	32,7
39,09	27,61	41,65	31,17	41,43	35,5	40,66	25,17	27,59
30,65	16,76	69,96	25,86	32,92	38,5	42,65	16,03	37,32
31,44	26,9	72,32	15,38	33,91	35,89	28,13	22,06	31,97
29,35	19,07	33,83	26,01	37,01	33,71	45,63	24,44	32,26
23,4	23,14	53,51	22,85	26,54	21,92	47,02	17,97	18,96
28,49	15,35	32,62	22,16	24,64	35,98	40,32	15,27	18,82
30,97	20,25	59,31	20,69	22,68	33,18	43,88	24,31	35,23
39,5	28,42	75,67	22,28	36,07	24,65	72,47	23,08	25,18
24,88	55,51	15,54	27,62	29,05	54,94	18,65	16,88	29,79

Статистический анализ данных с помощью пакета программ “STATISTICA”

Статистический анализ крупных баз данных связан с большими вычислительными затратами. В этом анализе полезно использовать пакет программ “STATISTICA”, который позволяет найти статистические оценки всех числовых характеристик генеральной совокупности, проверить статистическую гипотезу о нормальном распределении генеральной совокупности, построить соответствующую гистограмму распределения частот.

В случае двумерной выборки из нормальной генеральной совокупности пакет помогает построить облако данных, сгруппировать данные в виде корреляционной таблицы, найти выборочное уравнение регрессии и проверить гипотезу об отсутствии корреляционной связи компонент выборки.

Если закон распределения двумерной генеральной совокупности неизвестен, а выборка имеет малый объем, то пакет программ “STATISTICA” позволяет проверить гипотезу об отсутствии ранговой корреляции Спирмена и Кендалла.

В случае многомерной выборки можно найти уравнение множественной регрессии и выяснить значимость каждой из независимых переменных. С помощью коэффициента ранговой конкордации Кендалла можно проверить гипотезу об отсутствии корреляции многомерной выборки в целом.

С помощью критериев Вальда-Вольфовица, Манна-Уитни и Колмогорова-Смирнова можно проверить гипотезу о совпадении законов распределения двух выборок малого объема.

Пакет программ “STATISTICA” позволяет провести кластерный анализ многомерных объектов в различных метриках, построить дерево классификаций, содержащее необходимое количество вершин ветвления и т.д.

Для оценки числовых характеристик генеральной совокупности: средней, среднего квадратического отклонения, асимметрии и эксцесса используются соответствующие исправленные выборочные оценки: средняя, среднее квадратическое отклонение, асимметрия и эксцесс

,

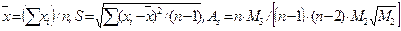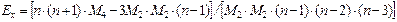, где М _к – центральные выборочные моменты к-го порядка. Все эти оценки можно найти в закладках “Statistics” ® “Basic Statistics” ® “Descriptive statistics” и в открывшемся окне необходимо поставить флажки около отмеченных оценок: “Mean”, “Standard Division”, “Skewness”, “Kurtosis”.

Для понимания процесса статистического оценивания важно провести расчеты «вручную» методом произведений (пример 3, тема 8 анонсированного практикума на стр. 75), сгруппировав предварительно данные, и сравнить полученные результаты с расчетами на ЭВМ.

Дата добавления: 2015-06-25