Вейвлет-анализ геофизических полей

Вейвлет-анализ представляет разложение исходных данных по системе заданных по форме сигналов и реализуется путем линейной свертки входных значений поля с весовыми функциями, в качестве которых выступают заданные по форме сигналы. Система заданных по форме сигналов или вейвлетов («вейвлет» - всплеск или небольшая волна, этот термин возник из применения вейвлет-анализа в самом начале его развития при обработке данных сейсморазведки) представляет совокупность таких функций (сигналов), каждая из которых является сдвинутой (по времени) и масштабируемой, т.е. сжатой или растянутой копией одной и той же функции, так называемого порождающего вейвлета. Для того, чтобы функция (сигнал) 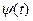называлась вейвлетом должны выполняться два условия: среднее значение 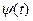равно нулю и 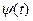должна быстро убывать при 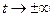, т.е. говорят, что всплеск (вейвлет) компактен в пространстве и локализован по частоте.

Вейвлет-анализ является обозначением большого класса разложений, поскольку существующие виды порождающих вейвлетов достаточно сильно отличаются друг от друга своими определениями, свойствами и приложениями. В определенном смысле вейвлет-анализ подобен Фурье-анализу с его разложением исходных значений по системе синусов и косинусов. Однако вейвлет-анализ имеет два существенных отличия от Фурье-анализа. Во-первых, Фурье-анализ не различает сигналы из двух синусоид с разными частотами, один из которых является суммой синусоид, а второй представляет следующие друг за другом последовательно синусоиды. В обоих случаях спектры таких сигналов представлены двумя пиками на фиксированных частотах этих синусоид. Во-вторых, Фурье-анализ слабо приспособлен для обработки нестационарных сигналов, в том числе локализованных на некотором временном интервале, поскольку в спектре теряется информация о временных характеристиках сигнала, т.е. вейвлет-анализ реализует спектральный анализ одновременно и по частоте и по времени. Порождающие или базисные функции вейвлет-анализа в отличие от Фурье-анализа обладают частотно-временной локализацией. Базисной функцией в Фурье-анализе является 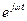. Масштабирование базисной функции по времени осуществляется в вейвлет-анализе умножением (или делением) ее абсциссы на число, т.е. 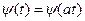, что приводит к сжатию или растяжению базисной функции, т.е. заданного по форме сигнала, то же самое касается масштабирования спектра по частоте.

В практике обработки геофизических данных получил применение непрерывный вейвлет-анализ. Непрерывным вейвлет-анализом (преобразованием) исходной функции f(t) называют функцию двух переменных 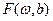. При этом вводится базис (порождающий вейвлет), отвечающий условиям равенства его среднего значения нулю и быстрого затухания по времени в виде

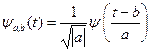(5.18),

где множитель 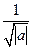требуется для сохранения масштабов. Если a и b – произвольные вещественные значения, тогда пара преобразований непрерывного вейвлет-анализа принимает вид:

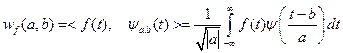(5.19)

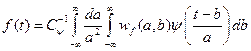, где 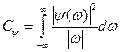- нормализующий множитель, 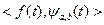- скалярное произведение исходного сигнала 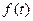с материнским вейвлетом 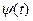, представленное их линейной сверткой.

Сравнивая формулы (6.9) с парой преобразований Фурье (5.15), легко видеть, что в преобразованиях Фурье роль функции 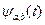играет функция 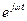, а 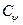аналогичен коэффициенту 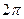, роль частоты играет масштабный множитель 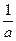. Но базисная функция 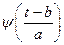зависит еще от параметра ее сдвига по времени b. Следовательно, для каждой пары значений a и b функция 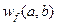определяет амплитуду соответствующего вейвлета. В Фурье-анализе каждой частоте соответствует всего одна гармоническая составляющая, а для вейвлет-анализа каждой частоте соответствует множество сдвинутых друг относительно друга функций.

В геофизике широко используются порождающие вейвлеты на основе производных функции Гаусса: 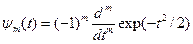, как хорошо локализованной и по частоте и по времени.

На рис.5.2. приведены WAVE-вейвлет при m =1 (а), MHAT-вейвлет при m=2 (б), DOG-вейвлет, как разность двух гауссиан (в), Morlet-вейвлет: 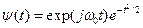(г)

Слева от этих вейвлетов представлены их Фурье-образы. Морле-вейвлет наиболее распространен при обработке данных сейсморазведки. МНАТ-вейвлет – при обработке данных электромагнитных зондирований.

.  

Рис.5.2. Основные типы вейвлетов и их Фурье-образы.

ГЛАВА VI. ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ ГЕОФИЗИЧЕСКИХ ПОЛЕЙ.

Одной из основных задач обработки геофизических полей является выделение сигналов (аномалий) на фоне помех. С этой целью используется большое разнообразие приемов преобразования исходного поля, которые сводятся к линейной или нелинейной фильтрации.

Под фильтрацией понимается преобразование экспериментальных данных для разделения сигналов и помех. Сигнал – это форма проявления поля, в которую облечена полезная информация. Помеха – любое возмущение поля, препятствующее выделению полезной информации. Для потенциальных полей употребляется термин аномалия, в сейсморазведке – сигнал, в электромагнитных методах используются оба термина.

В настоящее время наиболее широкое распространение получили линейные фильтры, построение которых осуществляется обычно в рамках аддитивной модели поля, т.е. когда результаты наблюдений 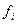представлены в виде суммы сигнала 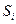и 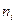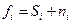. Следует отметить, что понятия сигнала и помехи в разведочной геофизике носят не абсолютный, а относительный характер. Так, при выделении локальной аномалии в гравиразведке помехами являются региональная аномалия и погрешности наблюдений, а при выделении региональной аномалии в качестве помех выступают уже локальные аномалии.

Сигнал (аномалия) может быть представлен либо детерминированной, т.е. аналитически заданной функцией, либо случайным процессом. Помеха чаще всего описывается случайным стационарным процессом с известными или неизвестными корреляционными (спектральными) свойствами. Помехи могут быть геологического (влияние фундамента, верхней части разреза, рельефа местности и т.д.) и негеологического (временные вариации полей, блуждающие токи, погрешности измерений и т.д.) происхождения.

Дата добавления: 2015-06-26