
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Одномерная адаптивная фильтрация
|
|
|
|
Начнем с рассмотрения самого простого, профильного варианта адаптивного фильтра, учитывающего нарушение стационарности поля вдоль профиля наблюдений. Алгоритм построения обычного одномерного линейного оптимального фильтра сводится к следующей процедуре:
§ по значениям поля на профиле наблюдений оценивается автокорреляционная функция R(m).
§ выбирается размер окна фильтрации n по значению радиуса корреляции r0.
§ в зависимости от критерия оптимальности фильтра, на основе имеющийся информации о параметрах корреляционных свойствах) полезного сигнала и помех, или на основе их оценок по значениям поля на профиле, вычисляются весовые коэффициенты конкретного оптимального фильтра 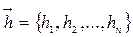 .
.
§ далее осуществляется свертка значений поля на профиле с весовыми коэффициентами фильтра в скользящем окне фиксированного размера.
Очевидно, что оценки параметров сигнала и помехи, полученные по данным всего профиля, для нестационарных полей не являются состоятельными, и соответственно весовые коэффициенты линейного фильтра, вычисленные на их основе, не будут адекватными конкретному критерию оптимальности. Так, структура автокорреляционной функции, рассчитанной по всему профилю наблюдений, отражает корреляционные характеристики наиболее энергоемких аномалий на профиле. Соответственно, в результате энергетической фильтрации, базирующейся на оценки автокорреляционных функции входного сигнала при некоррелируемой помехе, оптимальным образом будут оценены параметры именно этих аномалий. Для оценки параметров менее энергоемких аномалий, то есть аномалий с другими спектрально- корреляционными характеристиками, необходима повторная фильтрация остаточного поля, за которое принимается разность между исходным полем и результатом первой фильтрации.
Отметим, что для стационарных процессов вообще невозможно механическое перенесение понятий, разработанных для стационарных процессов. Такие понятия, как автокорреляция и спектр, имеющие определенный смысл для стационарных наблюдений, нуждаются в определении для нестационарных.

|
| Рис.6.1. Иллюстрация изменения формы автокорреляционной функции наблюденного поля вдоль профиля. |
Пример, наглядно иллюстрирующий изменение корреляционных характеристик магнитного поля вдоль профиля, приведен на рисунке 1.1.
Здесь число точек наблюдения на профиле составляет 250. В верхней части рисунка изображены три автокорреляционные функции, рассчитанные по трем выборкам из 100 точек, расположенных соответственно в левой, центральной и правой частях профиля. Характер автокорреляционных функций свидетельствует о наличии существенных различий между ними.
Рассмотрим алгоритм построения одномерного энергетического фильтра, настраивающегося на изменение спектрально- корреляционных характеристик поля вдоль профиля непосредственно в процессе фильтрации и позволяющего оценить форму аномалий на профиле с различными спектрально- корреляционными характеристиками, не прибегая к повторной фильтрации остаточного поля (адаптивный фильтр). Существо алгоритма заключается в следующем:
1. Как и в случае обычной энергетической фильтрации с целью оценки корреляционных характеристик наиболее энергоемких (как правило наиболее протяженных) аномалий на профиле рассчитывается автокорреляционная функция R(m) по всему профилю наблюдения.
2. По значению радиуса корреляции r0 выбирается размер так называемого базового окна[7] адаптивного фильтра 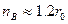
 ,который заведомо больше ширины наиболее энергоемкой (чаще всего и протяженной) составляющей поля на профиле.
,который заведомо больше ширины наиболее энергоемкой (чаще всего и протяженной) составляющей поля на профиле.
3. Базовое окно размещается в левой части профиля и в его окрестностях выполняется процедура обыкновенной энергетической фильтрации, которая сводится к оценке автокорреляционной функции R(m) (по значениям поля в базовом окне), определению длинны текущего окна фильтрации nT и весовых коэффициентов фильтра 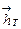 из уравнения [Rs-
из уравнения [Rs- 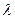 max I]
max I] 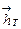 =0 (здесь Rs - оценка корреляционной матрицы аномалии размерности nT ,
=0 (здесь Rs - оценка корреляционной матрицы аномалии размерности nT , 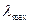 -максимальное собственное значение матрицы Rs I – единичная матрица).
-максимальное собственное значение матрицы Rs I – единичная матрица).
4. Затем осуществляется свертка исходного поля с весовыми коэффициентами фильтра 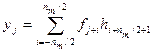 , результат которой относится к центральной точке базового окна.
, результат которой относится к центральной точке базового окна.
5. Базовое окно сдвигается на пикет вдоль профиля наблюдений, и процедура повторяется, начиная с третьего пункта.
Таким образом, в предложенном алгоритме для получения профильтрованного значения поля в каждой точке профиля выбираются собственные параметры фильтра - длина окна фильтрации и весовые коэффициенты фильтра. При этом характеристики фильтра настраиваются на оценки параметра наиболее энергоемких аномалий в окрестностях базового окна в отдельной точке наблюдений. Так, если в окрестностях точки отсутствуют аномалии, то ширина окна фильтрации будет минимальной, и весовые коэффициенты фильтра будут определятся спектрально-корреляционными характеристиками помехи. При наличии в окрестности точки самых протяженных аномалий ширина окна фильтрации будет максимальной и, соответственно, весовые коэффициенты фильтра будут определяться спектрально-корреляционными характеристиками этих аномалий.
Покажем преимущества адаптивного энергетического фильтра на примере обработки конкретных данных. На рисунке 6.2(а) изображен график вертикальной составляющей магнитного поля 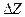 . В левой части графика присутствует протяженная положительная аномалия, а в правой - две положительные аномалии меньших размеров.
. В левой части графика присутствует протяженная положительная аномалия, а в правой - две положительные аномалии меньших размеров.
1 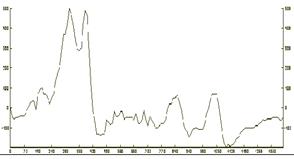 Рис.6.2(a). Наблюденное магнитное поле dZ.
Рис.6.2(a). Наблюденное магнитное поле dZ.
|
 Рис.6.2(b). Результат первой фильтрации исходного поля. Рис.6.2(b). Результат первой фильтрации исходного поля.
| |||
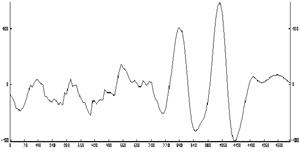 2Рис.6.2(c). Результат фильтрации остаточного поля. 2Рис.6.2(c). Результат фильтрации остаточного поля.
|
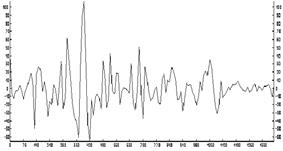 3Рис.6.2(d). Остаточное поле после второй фильтрации. 3Рис.6.2(d). Остаточное поле после второй фильтрации.
| |||
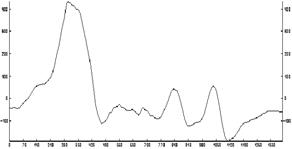 Рис.6.2(e). Результат адаптивной фильтрации исходного поля.
Рис.6.2(e). Результат адаптивной фильтрации исходного поля.
|  4Рис.6.2(g). Остаточное поле после адаптивной фильтрации. 4Рис.6.2(g). Остаточное поле после адаптивной фильтрации.
| |||
На рисунках 6.2(b), 6.2(c), 6.2(d) приведены результаты фильтрации исходного поля обычным энергетическим фильтром соответственно: результат фильтрации исходного поля, остаточного поля после первой фильтрации и остаточное поле после второй фильтрации. На рисунках 6.2(e) и 6.2(g) изображены соответственно результат фильтрации поля адаптивным энергетическим фильтром и остаточное поле. Анализ полученных результатов показывает, что после первой обычной фильтрации представляется возможным оценить лишь форму наиболее энергоемкой аномалии в левой части профиля (рис. 6.2(b)).
Параметры менее энергоемких аномалий, расположенных в правой части профиля, определяются лишь после повторной фильтрации остаточного поля рис.6.2(c). В то же время, с помощью алгоритма адаптивной энергетической фильтрации, возможна корректная оценка параметров сразу двух типов аномалий рис.6.2(e). Совпадение остаточных составляющих на рисунках рис.6.2(d) и рис.6.2(g) является подтверждением правильности основных принципов построения адаптивного алгоритма.
Рассмотренный алгоритм адаптивной одномерной энергетической фильтрации профильных наблюдений можно легко модифицировать для реализации других оптимальных линейных фильтров, для чего необходимо изменить лишь способ расчета весовых коэффициентов фильтра.
|
|
|
|
|
Дата добавления: 2015-06-26; Просмотров: 784; Нарушение авторских прав?; Мы поможем в написании вашей работы!