Понятие о линейном фильтре. Оператор свертки

Преобразование экспериментальных данных 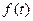в некоторую функцию 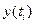производится путем применения оператора фильтра L: 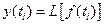, где 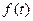- вход фильтра, 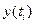- выход фильтра. Линейным оператором или линейным фильтром называется оператор, удовлетворяющий двум условиям:

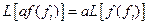
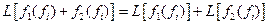
Воздействие линейного фильтра на входной сигнал f(t) задается выражением 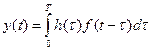, где 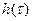- весовая функция фильтра, которое называется интегралом свертки. Дискретным аналогом свертки является ее представление в виде

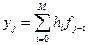(6.1),

где 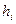- дискретные значения весовой функции фильтра (весовые коэффициенты) i =0,1,…, M. f_j – входные (исходные) значения, т.е. результаты фильтрации j =0,1,….., n. (M << n).

Основная задача линейной фильтрации состоит в определении весовой функции фильтра h_i. Заметим, что если в качестве весовых коэффициентов используются непосредственно сами исходные данные f_i, то выражение (6.1) приводит к реализации нелинейного фильтра. Так, если 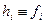, то (6.1) представляет автокорреляционную функцию, и, таким образом, расчет АКФ является нелинейной процедурой.

Суть операции свертки (6.1) легко пояснить на следующем примере. Пусть входная функция, т.е. исходные данные заданы тремя дискретными значениями f₀, f₁ и f₂, а весовая функция – двумя дискретными значениями h₀, h₁. В соответствии с выражением свертки (6.1) получаем:

при j =0 y₀ = h₀f₀

при j =1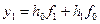

при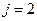

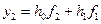
при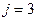

Процесс вычисления выходных значений свертки можно представить в виде следующей схемы

f₀ f₁ f₂

→ h₁ h₀

h₁ h₀

h h₀

h₁ h₀ →

Таким образом, операция свертки выполняется в четыре этапа: обращение во времени весовой функции, ее перемещение вдоль исходных (входных) значений поля, перемножение весовых коэффициентов с входными значениями и суммирование полученных произведений.

Общее число выходных значений 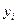равно n + M -1. Крайние члены выходных значений (для рассмотренного примера 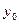и 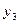) получаются при неполном перекрытии входного сигнала и весовой функции, т.е. их значения обычно искажены. Это – так называемые краевые эффекты. При обработке обычно их не учитывают, т.е. отбрасывают.

Проблема построения фильтра состоит в нахождении весовой функции, исходя из выбранной модели экстремальных данным, цели обработки и априорной информации о сигнале и помехах.

Используя свойство преобразований Фурье о свертке, можно перейти к частотному аналогу уравнения свертки, т.е.

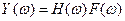(6.2)

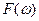где и 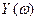- спектры входного и выходного сигналов, а 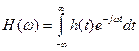- есть частотная характеристика линейного фильтра.

При дискретном задании весовой функции ее частотная характеристика определяется дискретным преобразованием Фурье. Обратное преобразование Фурье позволяет найти весовую функцию фильтра 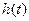, если задана его частотная характеристика .

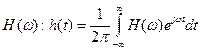При этом амплитудный спектр выходного сигнала 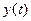равен произведению амплитудных спектров 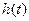и 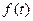, а фазовый спектр – сумме их фазовых спектров, т.е.

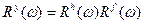
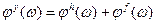
В общем случае частотная характеристика 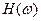является комплексным спектром, т.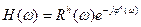е. , где 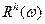есть амплитудно-частотная характеристика фильтра, называемая также коэффициентом передачи линейной системы, 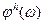- частотно-фазовая характеристика фильтра.

Амплитудно-частотная характеристика определяет величину усиления для составляющих сигнала определенной частоты при ее прохождении через линейный фильтр. Частотно-фазовая характеристика определяет временную задержку для составляющих, создаваемую фильтром на заданной частоте.

Фильтры, построение которых проводится в частотной области, делятся на

1.Низкочастотные, амплитудно-частотная характеристика 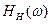которых имеет постоянное усиление в полосе частот 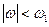и нулевое вне этой полосы.

2.Высокочастотные, амплитудно-частотная характеристика 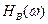которых постоянна в полосе 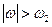и равна нулю вне этой полосы.

3.Полосовые, обеспечивающие равномерное усиление в полосе частот 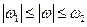и нулевое усиление за пределами этой полосы.

Частоты 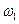и 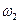являются граничными частотами или частотами среза фильтра.

Основой построения (или синтеза) фильтров любого типа является низкочастотный фильтр, поскольку через его амплитудно-частотную характеристику выражаются другие типы фильтров. Так, для высокочастотного фильтра 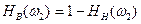, а для полосового фильтра .

Дата добавления: 2015-06-26