Искусство производить измерения

Предметное поле	Математика, литература, история, русский язык, черчение, воспитательная работа
Класс	9-11
Типология	Обучающая
Личностно-значимый познавательный вопрос	По своему правы те, кто говорит, что тригонометрия в реальной жизни не нужна. Ну, каковы ее обычные прикладные задачи? Измерять расстояние между недоступными объектами. С помощью тригонометрии составляют карты, измеряют высоту гор или деревьев, ширину рек и озер, расстояния до звезд. Простому дворнику все эти измерения и не нужны. Но однажды у нас сломался старенький бабушкин телевизор со стеклянным экраном и электронно-лучевой трубкой. И решили мы купить новый, жидкокристаллический. Старый телевизор был 29 дюймов по диагонали. Идем мы в магазин и покупаем бабушке новый телевизор. 29 дюймов сейчас не делают, возьмем 32, пусть бабушка порадуется. Приносим подарок, включаем, а бабушка нам и говорит: «Чой-то маленький какой-то телевизор, мой-то больше был, милые!» Можно было бы эти бабушкины высказывания пропустить мимо ушей, но мы знаем тригонометрию (!) и решили разобраться в этом вопросе. У старого телевизора отношение сторон – 4:5, а у нового – 9:16. Высота экрана бабушкиного телевизора была чуть больше 18 дюймов, а мы ей купили экран с высотой менее 16 дюймов. Вот он ей и кажется маленьким. Интернет-блогер Матвей Павлов Как мы это посчитали? Давайте разбираться в этой ситуации вместе. А где ещё в реальной жизни Вам могут пригодиться знания из тригонометрии?
Информация по данному вопросу	Текст 1. Определение синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника: Синусом α острого угла прямоугольного треугольника называется отношение AB/OB (противолежащего катета к гипотенузе). 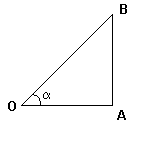Косинусом α острого угла прямоугольного треугольника называется отношение ОА/OB (прилежащего катета к гипотенузе). Тангенсом α острого угла прямоугольного треугольника называется отношение AB/OA (отношение противолежащего катета к прилежащему). Учебник «Геометрия 7-9 класс» Текст 2 . В строительстве очень важно знать площадь участка, отведённого на застройку. Для измерения площади древние египтяне использовали особый треугольник, у которого были фиксированные длины сторон. Занимались измерениями особые специалисты, которые назывались «натягивателями каната» (гарпедонаптай). Они брали длинную верёвку, делили её на 12 равных частей узелками или какими – то другими метками, а концы верёвки связывали. На направлении север – юг они устанавливали два кола на расстоянии четырёх частей, отмеченных на верёвке. Затем при помощи третьего кола натягивали связанную верёвку так, чтобы образовался треугольник, у которого одна сторона имела три части, другая – четыре, а третья пять частей. Получался прямоугольный треугольник, площадь которого могла быть принята за эталон, если ремесленники пользовались верёвкой всегда одной и той же строго определённой длины. При этом одна сторона, имеющая три части, указывала восточно-западное направление. История математики, 2012 год Текст 3. «- Сегодня нам надо измерить высоту площади далёкого Вида, – сказал инженер. – Вам понадобится для этого инструмент? – спросил Герберт. - Нет, не понадобится. Мы будем действовать несколько иначе, обратившись к не менее простому и точному способу. Юноша, стараясь научиться возможно большему, последовал за инженером, который спустился с гранитной стены до окраины берега. Взяв прямой шест, футов 12 длиною, инженер измерил его возможно точнее, сравнивая со своим ростом, который был ему хорошо известен. Герберт же нес за ним отвес, вручённый ему инженером: просто камень, привязанный к концу веревки. Не доходя футов 500 до гранитной стены, поднимавшейся отвесно, инженер воткнул шест в песок фута на 2 и, прочно укрепив его, поставил вертикально с помощью отвеса. Затем он отошёл от шеста на такое расстояние, чтобы, лёжа на песке, можно было на одной прямой линии видеть и конец шеста, и край гребня. Эту точку он тщательно пометил колышком. - Тебе знакомы начатки геометрии? – спросил он Герберта, поднимаясь с земли. - Да. - Помнишь свойства подобных треугольников? - Их сходственные стороны пропорциональны. - Правильно. Так вот, сейчас я построю два подобных прямоугольных треугольника. У меньшего одним из катетов будет отвесный шест, другим – расстояние от колышка до основания шеста; гипотенуза же – мой луч зрения. У другого треугольника катетами будут отвесная стена, высоту которой мы хотим определить, и расстояние от колышка до основания этой стены; гипотенуза же – мой луч зрения, совпадающий с направлением гипотенузы первого треугольника. - Понял! – воскликнул юноша. – Расстояние от колышка до шеста так относится к расстоянию от колышка до основания стены, как высота шеста к высоте стены. - Да. И следовательно, если мы измерим два первых расстояния, то зная высоту шеста, сможем вычислить четвёртый, неизвестный член пропорции, то есть высоту стены. - Оба горизонтальных расстояния были измерены: меньшее равнялось 15 футам, большее – 500 футам. По окончании измерений инженер составил следующую запись: 15: 500 = 10: х, 500 × 10 = 5000, 5000: 15 = 333,8. Значит, высота гранитной стены равнялась 333 футам». Ж.Верн «Таинственный остров» Текст 4. Наибольшее внимание ученых привлекали тригонометрические соотношения на сферических поверхностях. Это было продиктовано нуждами астрономии и географии. Дело в том, что преобладающей гипотезой о строении вселенной была геоцентристская. Согласно этой гипотезе земля есть шар, расположенный в центре небесной сферы, которая равномерно вращается вокруг своей оси. Светила расположены на этой сфере. Их движения и подвергаются изучению. При этом большое значение приобретают математические задачи о расположении точек и фигур на сферах и об их движениях (перемещениях). Работы, в которых подобные задачи решаются, получили название сферики. В сферику включались теоремы об окружностях и сферах, графические приемы построения сферических треугольников, сферопея или объединение кинематических моделей, изображающих мир (армиллы), и др. В сферике, таким образом, сочетались элементы практической астрономии, географии (определение места наблюдения, направления пути по положению небесных светил) и геометрии на сферах. Плоская тригонометрия при таких условиях отнюдь не играла лишь второстепенную роль по сравнению с тригонометрией сферической. У нее была своя область приложений. Кроме того, она являлась частью практической астрономии, так как в последней широко используются ортогональные проектирования. Фигуры, находящиеся или передвигающиеся на сфере, проектируются на плоскости, избранные для отсчетов: плоскости горизонта, меридиана или др. Тем самым многие задачи сводятся к плоским случаям. Измерительные операции при этом чаще всего прилагаются к хордам. Многократное применение подобных операций неизбежно порождало стремление табулировать значения хорд, составлять таблицы их значений. Сипливец Алексей, г. Нежина Текст 5. Синус – одна из тригонометрических функций, обозначение sin. Синус острого угла в прямоугольном треугольнике называется отношение катета, лежащего против этого угла, к гипотенузе. Индийские математики Синус обозначали словом «джива» (буквально — тетива лука). Арабы переделали этот термин в «джиба», который в дальнейшем превратился в «джайб» — обиходное слово арабского языка, означающее изгиб, пазуха, складка одежды, что соответствует латинскому слову sinus. Большая советская энциклопедия, 1969—1978
	Задания для работы и информацией
Ознакомление	Дайте лексическое толкование слова «Джайб».
Понимание	Постройте египетский треугольник с помощью циркуля и линейки без шкалы. Опишите шаги, необходимые для его построения. Предложите Герберту способ измерения высоты гранитной стены, позволяющий использовать определение синуса угла.
Применение	Проанализируйте особенности построения углов в 30°, 60°, 45° на основе определения синуса, косинуса и тангенса углов. Предложите дизайнеру несколько способов построения таких элементов в дизайне помещений.
Анализ	Разработайте план (эскиз) комнаты школьника, позволяющий показать применение нестандартных элементов дизайна интерьера.
Синтез	Проведите экспертизу ситуации с телевизором. Сделайте расчёты, доказывающие праводу рассуждений Матвея Павлова.
Оценка	Оцените значимость тригонометрических знаний для реальной жизни. Запишите свои рассуждения в форме связного текста.

Предметное поле	Математика, география, ОБЖ
Класс
Типология	Обучающая
Личностно–значимый познавательный вопрос	В современном мире мы определяем значения различных величин (длину, массу, температуру и т. п.) с помощью различных инструментов и приборов. Так, в своей профессиональной деятельности строители, архитекторы, лесоводы, военные для определения высоты объекта используют специальные сложные и дорогостоящие приборы – высотомеры. Можете ли Вы определить высоту здания или дерева без использования технических средств, полагаясь только на то, что есть «под руками»? Такое умение необходимо многим людям, находящимся в лесу: туристам, охотникам, лесникам.
Информация по данному вопросу	Текст 1. С пропорциями имели дело древние строители. Правильные соотношения, возводимых ими дворцов и храмов придавало этим зданиям ту необыкновенную красоту, которая восхищает нас и сегодня. Древнегреческие математики очень искусно преобразовывали пропорции, доказывали с их помощью самые сложные утверждения, решали самые сложные задачи. Говорят, что отрезки AB и СD пропорциональны отрезкам A₁B₁ и C₁D₁, если 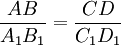. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. Коэффициентом подобия называется число k, равное отношению сходственных сторон. Признаки подобия треугольников: I. Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого. II. Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, лежащие между ними, равны. III. Два треугольника подобны, если три стороны одного треугольника пропорциональны трём сторонам другого треугольника. Отношение периметров двух подобных треугольников равно коэффициенту подобия. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. Источник: Атанасян Л. С., Геометрия 7-9 класс Текст 2. Измерение высоты дерева с помощью лужи можно удачно применять после дождя (в случае, когда луж нет, можно использовать зеркало). Измерение производят таким образом: находят невдалеке от измеряемого предмета лужицу и становятся около неё так, чтобы она помещалась между вами и предметом. После этого находят точку, из которой видна отражённая в воде вершинка предмета. Измеряемый предмет, например дерево, будет во столько раз выше вас, во сколько расстояние от него до лужицы больше, чем расстояние от лужицы до вас. Источник: http://piterhunt.ru Текст 3. Притча о Фалесе. Усталый пришел северный чужеземец в страну Великого Хапи. Солнце уже садилось, когда он подошел к великолепному дворцу фараона, что-то сказал слугам. Те мгновенно распахнули перед ним двери и провели его в приемную залу. И вот он стоит в запыленном походном плаще, а перед ним на золоченном троне сидит фараон. Рядом стоят высокомерные жрецы, хранители вечных тайн природы. – Кто ты? – спросил верховный жрец? – Зовут меня Фалес. Родом я из Милета. Жрец надменно продолжал: – Так это ты похвалялся, что сможешь измерить высоту пирамиды, не взбираясь на нее? – жрецы согнулись от хохота. – Будет хорошо, – насмешливо продолжал жрец, – если ты ошибешься не более, чем на сто локтей. – Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра. Лица жрецов потемнели. Какая наглость! Этот чужестранец утверждает, что может вычислить то, чего не могут они – жрецы Великого Египта. – Хорошо, сказал фараон. – Около дворца стоит пирамида, мы знаем ее высоту. Завтра проверим твое искусство. На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Провёл некоторые измерения и назвал высоту пирамиды. Источник: http://www.myshared.ru
Задания на работу с данной информацией
Ознакомление	1. Отрезки AB,CD и EF,MN пропорциональны друг другу. Найти EF,если AB= 5 см, CD= 80 мм, MN= 1 дм. 2. Что показывает коэффициент подобия? 3. Если в определении подобных треугольников поменять условие и заключение, будет ли оно верным? 4. Площадь одного подобного треугольника в четыре раза больше площади другого. Найдите коэффициент подобия. 5. Подобны ли треугольники ABC и A₁B₁C₁, если известно, что: AB=10 см, BC=8 см, A₁B₁=5 см, A₁C₁=3 см, ÐC=ÐC1=90⁰?
Понимание	Короткое плечо шлагбаума имеет длину 1м, а длинное плечо 4м. На какую высоту (в метрах) поднимается конец длинного плеча, когда конец короткого опускается на 0,5м?
Применение	В деревне у бабушки растёт старый тополь, который Вам необходимо спилить. В 10 м от тополя стоит забор. Определите, упадёт ли тополь на забор, если в 8 м от дерева находится лужа, отойдя от которой на 1,5 м вы видите верхушку тополя (рост человека 1м 70 см).
Анализ	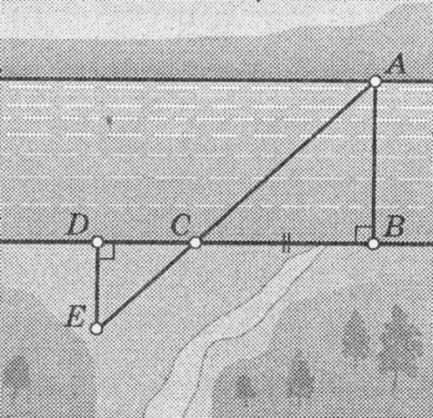Из воспоминаний участника Великой Отечественной войны: «Нашему отделению было приказано измерить ширину реки, через которую предстояло организовать переправу. Подобравшись к кустарнику вблизи реки, отделение залегло, а я вместе с другим солдатом выдвинулся ближе к реке, откуда был хорошо виден противоположный берег. В таких условиях измерить ширину реки можно было и на глаз. Но мы поступили следующим образом...» На рисунке показано, как можно определить ширину реки АВ, построив на местности подобные треугольники. Проанализируйте: какие построения выполнены; чем мы пользуемся для определения ширины реки? Выполните необходимые измерения и определите ширину реки (масштаб рисунка 1: 1000).
Синтез	Как, по Вашему мнению, Фалес вычислил высоту египетской пирамиды? Найдите её высоту, если высота шеста – 4 локтя; длина тени шеста – 6 локтей; длина тени пирамиды – 200 локтей.
Оценка	На каком оптимальном расстоянни от грядок необходимо построить домик высотой 6 м, чтобы грядки как можно больше времени были освещены солнцем.

учитель математики, МОАУ СОШ с УИОП №10, г. Киров