Непрерывность функции нескольких переменных

Введем важное вспомогательное понятие – понятие окрестности данной точки.

Окрестностью радиуса r точки М ₀(х ₀, у ₀) называется совокупность всех точек (х, у), удовлетворяющих неравенству 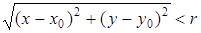, т.е. совокупность всех точек, лежащих внутри круга радиуса r с центром в точке М ₀(х ₀, у ₀).

Если мы говорим, что функция f (х, у) обладает каким-либо свойством «вблизи точки (х ₀, у ₀)» или «в окрестности точки (х ₀, у ₀)», то под этим подразумеваем, что найдется такой круг с центром (х ₀, у ₀), во всех точках которого данная функция обладает указанным свойством.

Прежде чем рассматривать понятие непрерывности функции нескольких переменных, рассмотрим понятие предела функции нескольких переменных.

Пусть дана функция

z = f (х, у),

y

определенная в некоторой области G плоскости Оху. Рассмотрим некоторую определенную точку М ₀(х ₀, у ₀), лежащую в области G или на ее границе (рис. 3).

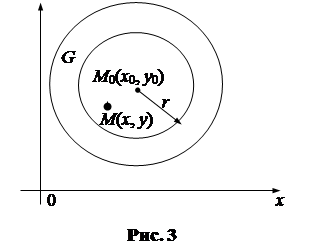Определение 4. Число А называется пределом функции f (х, у) при стремлении М (х, у) к точке М ₀(х ₀, у ₀), если для каждого число e > 0 найдется такое число r > 0, что для всех точек М (х, у), для которых выполняется неравенство 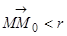, имеет место неравенство

.

Если число А является предел функции f (х, у) при М (х, у) ® М ₀(х ₀, у ₀), то пишут

.

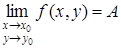Определение 5. Пусть точка М ₀(х ₀, у ₀) принадлежит области определения функции f (х, у). Функция z = f (х, у) называется непрерывной в точке М ₀(х ₀, у ₀), если имеет место равенство

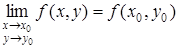, (2)

причем тоска М (х, у) стремится к точке М ₀(х ₀, у ₀) произвольным образом, оставаясь в области определения функции.

Если обозначим х = х ₀ + D х, у = у ₀ + D у, то равенство (2) можно переписать так:

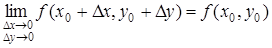(3)

или

. (4)

Обозначим 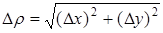. При D х ® 0 и D у ® 0 Dr ® 0, и обратно, если Dr ® 0, то D х ® 0 и D у ® 0.

Замечая, далее, что выражение, стоящее в квадратных скобках в равенстве (4), есть полное приращение функции D z, равенство (4) можно переписать в форме

.

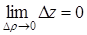Функция, непрерывная в каждой точке некоторой области, называется непрерывной в области.

Если в некоторой точке N (х ₀, у ₀) не выполняется условие (2), то точка N (х ₀, у ₀) называется точкой разрыва функции z = f (х, у). Условие (3) может не выполняться, например, в случаях:

1) z = f (х, у) определена во всех точках некоторой окрестности N (х ₀, у ₀), за исключением самой точки N (х ₀, у ₀);

2) функция z = f (х, у) определена во всех точках окрестности точки N (х ₀, у ₀), но не существует предел ;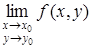

3) функция определена во всех точках окрестности N (х ₀, у ₀) и существует предел 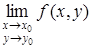, но .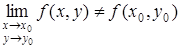

Пример 12. Функция z = х ² + у ² непрерывна при любых значениях х и у, т.е. в любой точке плоскости Оху.

Действительно, каковы бы ни были числа х и у, D х и D у, имеем

,

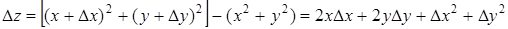следовательно, .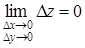

Приведем пример разрывной функции.

Пример 13. Функция 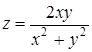определена всюду, кроме точки х = 0, у = 0.

Рассмотрим значения z вдоль прямой y = kx (k = const). Очевидно, вдоль этой прямой

,

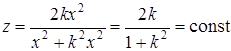т.е. функция z вдоль всякой прямой, проходящей через начало координат, сохраняет постоянное значение, зависящее от углового коэффициента k прямой. Поэтому, подходя к началу координат по различным путям, мы будем получать различные предельные значения, а это значит, что функция f (х, у) не имеет предела, когда точка (х, у) на плоскости Оху стремится к началу координат. Следовательно, функция разрывна в этой точке. Эту функцию нельзя доопределить в начале координат так, чтобы она стала непрерывной. Легко видеть, с другой стороны, что в остальных точках эта функция непрерывна.

Укажем некоторые важные свойства функции многих переменных, непрерывной в замкнутой и ограниченной области. Эти свойства аналогичны свойствам непрерывной на отрезке функции одной переменной.

Свойство 1. Если функция f (х, у, …) определена и непрерывна в замкнутой и ограниченной области D, то в области D найдется по крайней мере одна точка N (х ₀, у ₀, …) такая, что для всех других точек области будет выполняться соотношение

f (х ₀, у ₀, …) ³ f (х, у, …),

и по крайней мере одна точка Р (х ₁, у ₁, …) такая, что для всех других точек области будет выполняться соотношение

f (х ₁, у ₁, …) £ f (х, у, …).

Значение функции f (х ₀, у ₀, …) = М будем называть наибольшим значением функции f (х, у, …) в области D, а значение f (х ₁, у ₁, …) = т – наименьшим значением.

Это свойство формулируется и так. Непрерывная функция в замкнутой ограниченной области D достигает по крайней мере один раз наибольшего значения М и наименьшего значения т.

Свойство 2. Если функция f (х, у, …) непрерывна в замкнутой и ограниченной области D и если М и т – наибольшее и наименьшее значения функции f (х, у, …) в области, то для любого числа m, удовлетворяющего условию т < m < М, найдется в области такая точка Р^* (х ^*, у ^*, …), что будет выполняться равенство f (х ^*, у ^*, …) = m.

Следствие свойства 2. Если функция f (х, у, …) непрерывна в замкнутой ограниченной области и принимает как положительные, так и отрицательные значения, то внутри области найдутся точки, в которых функция f (х, у, …) обращается в нуль.

Задание для самостоятельной работы.

Найти точки разрыва следующих функций:

23. 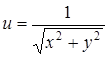.	24. .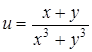
25. 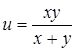.	26. .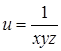
27. 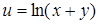.	28. .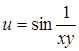

29. Показать, что функция 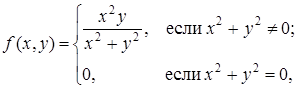вточке М (0; 0) непрерывна вдоль каждого луча 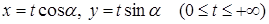, проходящего через эту точку, т.е. существует 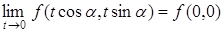; однако эта функция не является непрерывной в точке (0; 0).

30. Является ли функция 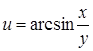непрерывной в своей области определения?

Дата добавления: 2015-06-04