Полное приращение и полный дифференциал

Функции двух переменных

Геометрическая интерпретация частных производных

Частная производная 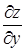численно равна тангенсу угла наклона касательной к кривой, получающейся в сечении поверхности z = f (х, у) плоскостью x = const.

Аналогично частная производная 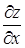численно равна тангенсу угла наклона касательной к сечению поверхности z = f (х, у) плоскостью у = const.

Задания для самостоятельной работы.

Найти частные производные , , :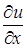

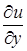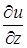31. 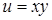.	32. .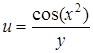
33. u = x^y.	34. .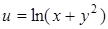
35. 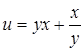.	36. .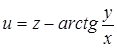
37. 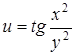.	38. .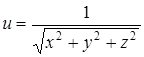
39. 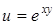.	40. .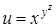

По определению полного приращения функции z = f (х, у) имеем

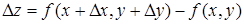. (5)

Предположим, что f (х, у) в рассматриваемой точке (х, у) имеет непрерывные частные производные.

Выразим D z через частные производные. Для этого в правой части равенства (5) прибавим и вычтем f (х, у + D у):

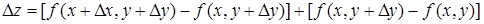. (6)

Выражение

f (х, у + D у) – f (х, у),

стоящее во второй квадратной скобке, можно рассматривать как разность двух значений функции одной переменной у (значение х остается постоянным). Применяя к этой разности теорему Лагранжа, получим

, (7)

где 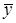заключено между у и у + D у.

Точно так же выражение, стоящее в первой квадратной скобке равенства (6), можно рассматривать как разность двух значений функции одной переменной х (второй аргумент сохраняет одно и то же значение у + D у). Применяя к этой разности теорему Лагранжа, получим

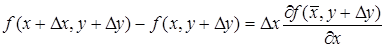, (8)

где 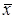заключено между х и х + D х.

Внося выражения (7) и (8) в равенство (2), получим

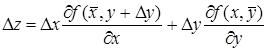. (9)

Так как, по предположению, частные производные непрерывны, то

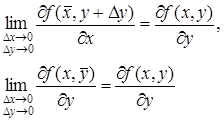(10)

(так как 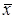и 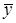заключены соответственно между х и х + D х, у и у + D у, то при D х ® 0 и D у ® 0 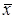и 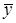стремятся соответственно к х и у). Равенство (10) можно переписать в виде

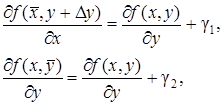(11)

где величины g₁ и g₂ стремятся к нулю, когда D х и D у стремятся к нулю (т.е. когда ).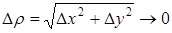

В силу равенства (11) соотношение (9) принимает вид

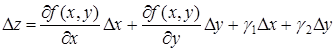. (12)

Сумма двух последних слагаемых правой части является бесконечно малой высшего порядка относительно 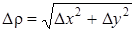. Действительно, отношение 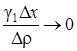при Dr ® 0, так как g₁ является бесконечно малой величиной, а 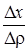- ограниченной 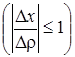. Аналогично проверяется, что .

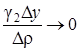Сумма первых двух слагаемых есть выражение, линейное относительно D х и D у. Пр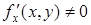и и 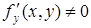это выражение представляет собой главную часть приращения, отличаясь от D z на бесконечно малую высшего порядка относительно .

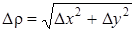Определение 7. Функция z = f (х, у), полное приращение D z которой в данной точке (х, у) может быть представлена в виде суммы двух слагаемых: выражения, линейного относительно D х и D у, и величины, бесконечно малой высшего порядка относительно Dr, называется дифференцируемой в данной точке, а линейная часть приращения называется полным дифференциалом и обозначается через dz или df.

Из равенства (12) следует, что если функция f (х, у) имеет непрерывные частные производные в данной точке, то она дифференцируема в этой точке и имеет полный дифференциал

.

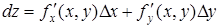Равенство (12) можно переписать в виде 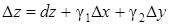и с точностью до бесконечно малых высшего порядка относительно Dr можно написать следующее приближенное равенство:

D z» dz. (13)

Приращения независимых переменных D х и D у мы будем называть дифференциалами независимых переменных х и у и обозначать соответственно через dx и dy. Тогда выражение полного дифференциала примет вид

. (14)

Таким образом, если функция z = f (х, у) имеет непрерывные частные производные, то она дифференцируема в точке (х, у), и ее полный дифференциал равен сумме произведений частных производных на дифференциалы соответствующих независимых переменных.

Пример 17. Найти полный дифференциал и полное приращение функции z = ху в точке (2; 3) при D х = 0.1, D у = 0.2.

Решение.

D z = (х + D х)(у + D у) – ху = у D х + х D у + D х D у,

.

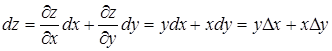Следовательно,

D z = 3×0.1 + 2×0.2 + 0.1×0.2 = 0.72, dz = 3×0.1 + 2×0.2 = 0.7.

Предыдущие рассуждения и определения соответственным образом обобщаются на функции любого числа аргументов.

Если имеем функцию любого числа переменных

w = f (x, y, z, u, …, t),

причем все частные производные 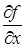, , 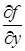…, 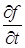непрерывны в точке (x, y, z, u, …, t), то выражение

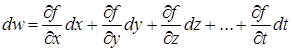
является главной частью полного приращения функции и называется полным дифференциалом. Доказательство того, что разность D w - dw является бесконечно малой более высокого порядка, чем 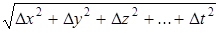, проводится совершенно так же, как и для функции двух переменных.

Пример 18. Найти полный дифференциал функции 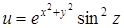трех переменных х, у, z.

Решение. Заметив, что частные производные

, ,

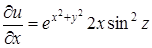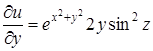непрерывны при всех значениях х, у, z, находим

.

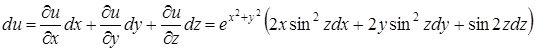Дата добавления: 2015-06-04