Применение полного дифференциала в приближенных вычислениях

Пусть функция z = f (х, у) дифференцируема в точке (х, у). Найдем полное приращение этой функции

,

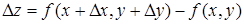откуда

. (15)

Подставляя в формулу (15) вместо D z, согласно (13), развернутое выражение для dz (14), получим приближенную формулу

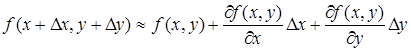(16)

верную с точностью до бесконечно малых высшего порядка относительно D х и D у.

Покажем, как используются формулы (13) и (16) для приближенных вычислений.

Пример 19. Вычислить объем материала, нужного для изготовления цилиндрического стакана следующих размеров (рис. 14): радиус внутреннего цилиндра R, высота внутреннего цилиндра Н, толщина стенок и дна стакана k.

		Рис. 4

Решение. Дадим два решения этой задачи: точное и приближенное.

Точное решение. Искомый объем v равен разности объемов внешнего цилиндра и внутреннего цилиндра. Так как радиус внешнего цилиндра равен R + k, а высота H + k, то

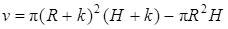или . (17)

Приближенное решение. Обозначим через f объем внутреннего цилиндра, тогда 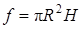. Это – функция двух переменных R и Н. Если увеличим R и Н на k, то функция f получит приращение D f; но это и будет искомый объем v, т.е. v = D f.

На основании соотношения (15) имеем приближенное равенство v» df, или 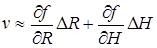. Но так как 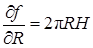, , 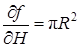D R = D Н = k, то получаем

. (18)

Сравнивая результаты (17) и (18), видим, что они отличаются на величину , состоящую из членов второго и третьего порядка малости относительно k.

Применим эти формулы к числовым примерам.

Пусть R = 4 см, Н = 20 см, k = 0.1 см.

Применяя (17), получим точно

.

Применяя формулу (18), получим приближенно

.

Следовательно, приближенная формула (18) дает ответ с погрешностью, меньшей 0.3p, что составляет 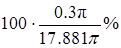, т.е. менее 2% измеренной величины.

Приложение дифференциала к оценке погрешности при вычислениях

Пусть некоторая величина и является функцией величин х, у, z, …, t:

и = f (x, y, z, …, t),

причем, определяя каким-то способом значения величин х, у, z, …, t, мы допускаем погрешности D х, D у, …, D t. Тогда значение и, вычисленное по неточным значениям аргументов, получится с погрешностью

D и = f (x + D х, y + D у, z + D z, …, t + D t) - f (x, y, z, …, t).

Ниже мы займемся оценкой погрешности D и, если известны погрешности D х, D у, …, D t.

При достаточно малых абсолютных значениях величин D х, D у, …, D t можем приближенно заменить полное приращение полным дифференциалом:

.

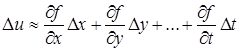Здесь значения частных производных и значения погрешностей аргументов могут быть как положительными, так и отрицательными. Заменяя их абсолютными величинами, получим неравенство

.

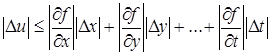Если через |D^* x |, |D^* y |, …, |D^* t |, |D^* u | обозначим максимальные абсолютные погрешности соответствующих величин (границы для абсолютных величин значений погрешностей), то можно, очевидно, принять

. (19)

Отношение погрешности D х некоторой величины к приближенному значению х этой величины называется относительной погрешностью величины. Будем его обозначать d х:

.

Максимальной относительной погрешностью величины х называется отношение максимальной абсолютной погрешности к абсолютной величине х и обозначается ½d^* х ½:

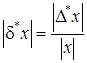. (20)

Для оценки максимальной относительной погрешности функции и разделим все числа равенства (19) на ½ и ½=½ f (x, y, z, …, t ½:

,

но

, , …, .

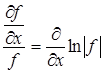Поэтому равенство (20) можно переписать так:

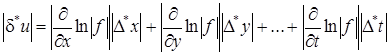, (21)

или коротко

.

Из формул как (20), так и (21) следует, что максимальная относительная погрешность функции равняется максимальной абсолютной погрешности логарифма этой функции.

Замечание. Если и = х – у, то 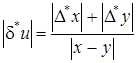. Если х и у близки, то может оказаться, что 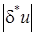будет очень велика по сравнению с определяемой величиной х – у. Это обстоятельство следует учитывать при производстве вычислений.

Задания для самостоятельной работы

Найти полный дифференциал и полное приращение функции u (x,y) в точке (2; 1) при D х = 0.1, D у = 0.1.

41. u = x+y.	42. .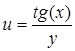
43. 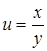.	44. .

Найти полный дифференциал функции трех переменных х, у, z.

45. 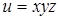.	46. .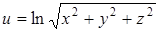
47. 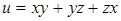.	48. .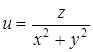

Заменяя приращение функции дифференциалом, приближенно вычислить:

49. 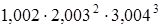.	50. .
51. 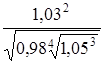.	52. .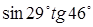

53. На сколько изменятся диагональ и площадь прямоугольника со сторонами

x = 6 м и y = 8 м, если первая сторона увеличится на 2 мм, а вторая сторона уменьшится на 5 мм?

54. При измерении радиуса основания R и высоты H цилиндра были получены следующие результаты:R=2,5±0,1 мм;Н=4,0±0,2 мм. Скакой абсолютной погрешностью D и относительной погрешностью d может быть вычислен объем цилиндра?

55. Стороны треугольника a =200 м ± 2 м, b =300 м ± 5 м и угол между ними

С = 60^о±1^о. С какой абсолютной погрешностью может быть вычислена третья сторона?

7. Производная сложной функции. Полная производная.

Полный дифференциал сложной функции

Дата добавления: 2015-06-04