Предположим, что в уравнении

z = F (u, v) (22)

и и v являются функциями независимых переменных х и у:

и = j(х, у), v = y(х, у). (23)

В этом случае z есть сложная функция от аргументов х и у.

Конечно, z можно выразить и непосредственно через х и у, а именно:

z = F (j(х, у), y(х, у)) (24)

Пример 20. Пусть z = u ³ v ³ + u + 1, u = x ² + y ², v = e^x+y + 1, тогда

z = (х ² + у ²)³(е^х+у + 1)³ +(х ² + у ²) + 1.

Предположим, что функции F (u, v), j(х, у), y(х, у) имеют непрерывные частные производные по всем аргументам и поставим задачу: вычислить 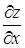, , 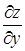исходя из уравнений (22) и (23) и не используя уравнение (24).

Дадим аргументу х приращение D х, сохраняя значение у неизменным. Тогда в силу уравнения (23) u и v получат приращения и .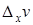

Но если u и v получают приращения и 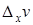, то и функция z = F (u, v) получит приращение D z, определяемое формулой (12):

.

Разделим все члены этого равенства на D х:

.

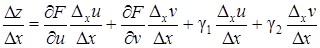Если D х ® 0, то ® 0 и 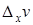® 0 (в силу непрерывности функций u и v). Но тогда g₁ и g₂ тоже стремятся к кулю. Переходя к пределу при D х ® 0, получим

, , , ,

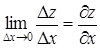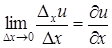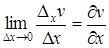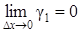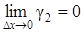
и, следовательно,

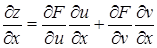. (25)

Если бы мы дали приращение D у переменной у, а х оставили неизменным, то с помощью аналогичных рассуждений нашли бы

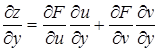. (26)

Пример 21. , , .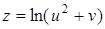

, , , , , .

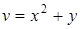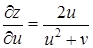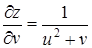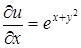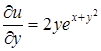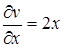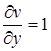Используя формулы (25) и (26), находим

,

.

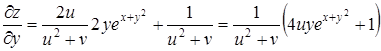В последнем выражении вместо u и v необходимо подставить 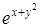и 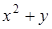соответственно.

Для случая большего числа переменных формулы (25) и (26) естественным образом обобщаются.

Например, если w = F (z, u, v, s) есть функция четырех аргументов z, u, v, s, а каждый из них зависит от х и у, то формулы (25) и (26) принимают вид

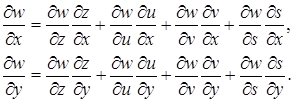(27)

Если задана функция z = F (x, y, u, v), где y, u, v в свою очередь зависят от одного аргумента х:

у = f (x), u = j(x), v = y(х),

то, по сути дела, z является функцией только одной переменной х и можно ставить вопрос о нахождении производной .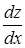

Эта производная вычисляется по первой из формул (27)

;

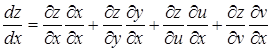но так как y, u, v – функции только одного х, то частные производные обращаются в обыкновенные, кроме того, 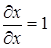; поэтому

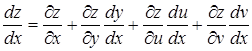. (28)

Эта формула носит название формулы для вычисления полной производной 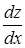(в отличие от частной производной ).

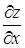Пример 22. , .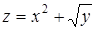

, , .

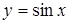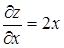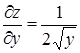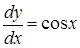Формула (28) дает в этом случае следующий результат:

.

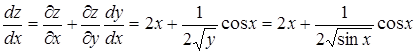Найдем далее полный дифференциал сложной функции, определенной равенствами (22) и (23).

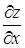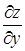Подставляя выражения и , определенные равенствами (25) и (26), в формулу полного дифференциала

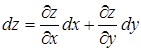. (29)

Дата добавления: 2015-06-04