
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Динамика. Формула Название формулы Расшифровка обозначений I–й закон Ньютона – ускорение тела;
|
|
|
|
| Формула | Название формулы | Расшифровка обозначений | ||

| I–й закон Ньютона |  – ускорение тела; – ускорение тела; 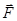 – равнодействующая сил, приложенных к телу. – равнодействующая сил, приложенных к телу.
| ||

| П–й закон Ньютона. |  – ускорение, с которым движется тело; – ускорение, с которым движется тело; 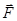 – равнодействующая сил, приложенных к телу; т – масса тела. – равнодействующая сил, приложенных к телу; т – масса тела.
| ||

| III–й закон Ньютона. |  – сила, с которой первое тело действует на второе; – сила, с которой первое тело действует на второе;  – сила, с которой второе тело действует на первое тело. – сила, с которой второе тело действует на первое тело.
| ||

| Закон Гука (1–й вид) |  – проекция силы упругости на ось X; k – жёсткость тела; х – величина деформации тела. – проекция силы упругости на ось X; k – жёсткость тела; х – величина деформации тела.
| ||

| Абсолютное удлинение | 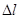 – абсолютное удлинение; l – конечная длина тела; – абсолютное удлинение; l – конечная длина тела;  – начальная длина тела – начальная длина тела
| ||

| Закон всемирного тяготения | F – модуль силы гравитационного взаимодействия двух тел; G – гравитационная постоянная;  – масса первого тела; – масса первого тела;  – масса второго тела: l – расстояние между центрами тел. – масса второго тела: l – расстояние между центрами тел.
| ||

| Сила тяжести |  – сила тяжести, действующая на тело; т – масса тела;. – сила тяжести, действующая на тело; т – масса тела;.  – ускорение свободного падения. – ускорение свободного падения.
| ||
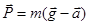
| Вес тела, движущегося с ускорением |  – вес тела; т – масса тела; – вес тела; т – масса тела;  – ускорение свободного падения; – ускорение свободного падения;  – ускорение, с которым движется тело. – ускорение, с которым движется тело.
| ||
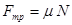
| Сила трения | Fmp – модуль силы трения, действующей на тело; 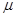 – коэффициент трения; N – модуль нормальной реакции опоры. – коэффициент трения; N – модуль нормальной реакции опоры.
| ||
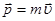
| Импульс тела | 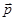 – импульс тела; т – масса тела; – импульс тела; т – масса тела;  – скорость тела. – скорость тела.
| ||

| Связь импульса силы и изменения импульса тела | 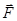 – сила, действующая на тело; t – время действия силы; – сила, действующая на тело; t – время действия силы;  – изменение импульса тела ( – изменение импульса тела ( = =  ) )
| ||

| Закон сохранения импульса | 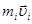 – импульс одного из взаимодействующих тел (под номером i) – импульс одного из взаимодействующих тел (под номером i)
| ||

| Механическая работа | А – работа силы; F – модуль силы, совершающей работу; s – модуль перемещения тела под действием силы; cos α – косинус угла между вектором силы и вектором перемещения | ||

| Кинетическая энергия | Ek – кинетическая энергия тела; т – масса тела; 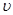 – модуль скорости тела. – модуль скорости тела.
| ||
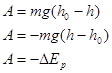
| Работа силы тяжести | А – работа силы тяжести; m – масса тела; g – ускорение свободного падения; h0 – высота начального положения тела над нулевым уровнем потенциальной энергии; h – высота конечного положения тела над нулевым уровнем потенциальной энергии. | ||

| Потенциальная энергия тела, поднятого над землёй | Еp – потенциальная энергия тела, поднятого над землёй; т – масса тела; g – ускорение свободного падения; h – высота тела над уровнем земли. | ||

| Теорема о потенциальной энергии | А – работа (силы тяжести, силы упругости); Δ Ep – изменение потенциальной энергии тела. | ||

| Потенциальная энергия упруго деформированного тела | Ер – потенциальная энергия упруго деформированного тела; k – жёсткость тела; х – величина деформации. | ||
 
| Работа силы упругости | А – работа силы упругости; х1 – величина деформации в исходном состоянии; х2 – величина деформации в конечном состоянии; k – жёсткость тела. | ||

| Закон сохранения механической энергии | Ek1, Epl – кинетическая и потенциальная энергия в начальном состоянии системы; Ek2, Еp2 – кинетическая и потенциальная энергия в конечном состоянии системы. | ||

| Мощность | N – мощность; А – работа; t – время совершения работы | ||
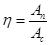
| Коэффициент полезного действия | η – коэффициент полезного действия; А„ – полезная работа; Аc – совершённая работа. | ||

| Момент силы | M – момент силы; F – сила, приложенная к телу; l – плечо силы. | ||

| (*)Условия равновесия твердого тела | 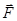 – равнодействующая сил, приложенных к телу; – равнодействующая сил, приложенных к телу;  – алгебраическая сумма моментов всех приложенных сил. – алгебраическая сумма моментов всех приложенных сил.
| ||

| Закон Архимеда | FA – сила Архимеда; 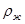 – плотность жидкости; g – ускорение свободного падения; Vж –объём жидкости, вытесненной телом – плотность жидкости; g – ускорение свободного падения; Vж –объём жидкости, вытесненной телом
| ||
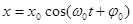
| Уравнение механических колебаний тела. | х – координата колеблющегося тела; х0 – амплитуда колебаний координаты;  – собственная циклическая частота; t – текущее время; – собственная циклическая частота; t – текущее время;  –начальная фаза колебаний. –начальная фаза колебаний.
| ||
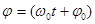
| Фаза колебаний | 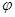 – фаза колебаний; – фаза колебаний;  – собственная циклическая частота; t – текущее время; – собственная циклическая частота; t – текущее время;  – начальная фаза колебаний – начальная фаза колебаний
| ||

| Собственная циклическая частота груза на пружине |  – собственная циклическая частота; k – жёсткость; т – масса груза – собственная циклическая частота; k – жёсткость; т – масса груза
| ||
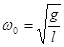
| Собственная циклическая частота математического маятника |  –собственная циклическая частота; g – ускорение свободного падения; l – длина математического маятника. –собственная циклическая частота; g – ускорение свободного падения; l – длина математического маятника.
| ||
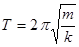
| Период колебаний тела под действием силы упругости | Т – период колебаний; k – жёсткость; т – масса груза. | ||

| Период колебаний математического маятника (формула Гюйгенса) | Т – период колебаний; l – длина математического маятника; g – ускорение свободного падения | ||
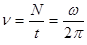
| Частота колебаний. |  – частота колебаний; N – число колебаний; t – время колебаний; – частота колебаний; N – число колебаний; t – время колебаний; 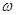 – циклическая частота. – циклическая частота.
| ||

| Связь периода и частоты колебаний | T – период колебаний;  – частота колебаний – частота колебаний
| ||

| Амплитуда скорости при колебаниях | 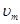 – амплитуда скорости колеблющегося тела; хm – амплитуда координаты; – амплитуда скорости колеблющегося тела; хm – амплитуда координаты;  – собственная циклическая частота колебательной системы. – собственная циклическая частота колебательной системы.
| ||
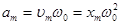
| Амплитуда ускорения при колебаниях | am – амплитуда ускорения колеблющегося тела; 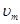 – амплитуда скорости колеблющегося тела; хm – амплитуда координаты; – амплитуда скорости колеблющегося тела; хm – амплитуда координаты;  – собственная циклическая частота колебательной системы. – собственная циклическая частота колебательной системы.
| ||

| Энергия механических колебаний | Е – полная энергия колебательной системы; Еp – потенциальная энергия взаимодействия тел колебательной системы; Ek – кинетическая энергия колебательной системы; Ерт– максимальная потенциальная энергия; Ekm– максимальная кинетическая энергия | ||

| Потенциальная энергия механической колебательной системы | Ер – потенциальная энергия механической колебательной системы; k – жёсткость; х – координата колеблющегося тела;  – собственная циклическая частота колебательной системы; хт – амплитуда координаты; t – текущее время. – собственная циклическая частота колебательной системы; хт – амплитуда координаты; t – текущее время.
| ||
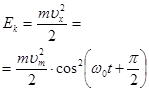
| Кинетическая энергия колебательной системы. | Ek – кинетическая энергия колебательной системы;  – проекция скорости колеблющегося тела на ось X; т – масса груза; – проекция скорости колеблющегося тела на ось X; т – масса груза;  – собственная циклическая частота колебательной системы. – собственная циклическая частота колебательной системы.
| ||
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 613; Нарушение авторских прав?; Мы поможем в написании вашей работы!