
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оценка параметров генеральной совокупности
|
|
|
|
Существуют точечные и интервальные оценки генеральных параметров.
Точечной называют оценку, которая определяется одним числом. К таким оценкам относятся, например,
– выборочная средняя 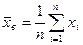 , или для сгруппированного вариационного ряда
, или для сгруппированного вариационного ряда  ;
;
– выборочная дисперсия  , или для сгруппированного вариационного ряда
, или для сгруппированного вариационного ряда  , или
, или  ;
;
– выборочное среднее квадратическое отклонение  и др.
и др.
Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны быть:
– несмещенными;
– эффективными;
– состоятельными.
Оценка называется несмещенной, если математическое ожидание ее выборочного распределения совпадает со значением генерального параметра.
Точечная оценка называется эффективной, если она имеет наименьшую дисперсию выборочного распределения по сравнению с другими аналогичными оценками, т.е. обнаруживает наименьшую случайную вариацию.
Точечная оценка называется состоятельной, если при увеличении объема выборочной совокупности  она стремиться к величине генерального параметра.
она стремиться к величине генерального параметра.
Например, выборочная средняя 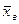 есть состоятельная, несмещённая оценка генеральной средней
есть состоятельная, несмещённая оценка генеральной средней  . Для выборки из нормальной генеральной совокупности эта оценка является также и эффективной.
. Для выборки из нормальной генеральной совокупности эта оценка является также и эффективной.
При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
Интервальной называют оценку, которая определяется двумя числами – концами интервала – доверительного интервала.
Интервальные оценки позволяют установить точность и надежность оценок.
Для оценки генерального параметра с помощью доверительного интервала необходимы три величины:
– значение выборочного показателя;
– критерий надежности  , или показатель безошибочных прогнозов, значение которого определяется заранее, при планировании исследования, исходя из представления о большей или меньшей ответственности возможных результатов работы;
, или показатель безошибочных прогнозов, значение которого определяется заранее, при планировании исследования, исходя из представления о большей или меньшей ответственности возможных результатов работы;
– ошибка репрезентативности  или показатель точности выборочного параметра определяется на основе выборочных данных по формулам математической статистики.
или показатель точности выборочного параметра определяется на основе выборочных данных по формулам математической статистики.
Например, доверительный интервал для генеральной средней 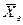 находится по формуле:
находится по формуле:  при уровне значимости
при уровне значимости 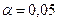 .
.
Пример 1. Частота пульса по данным медицинского осмотра 17 девочек – первоклассниц: 76, 70, 66, 68, 70, 72, 74, 76, 78, 70, 82, 68, 74, 70, 70, 70. Найти точечные оценки выборки и построить полигон относительных частот.
Решение:
1) Выполним ранжирование выборочных данных: 661, 682, 706, 721, 742, 763, 781,821.
2) Вероятность попадания в интервал вычисляется по следующей формуле 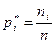 , где n – объем выборки, а ni – частота встречаемости i – го признака. Вычисления pi выполним в таблице:
, где n – объем выборки, а ni – частота встречаемости i – го признака. Вычисления pi выполним в таблице:
| X | 
| ||||||||
| ni | |||||||||
| pi | 0,06 | 0,12 | 0,35 | 0,06 | 0,12 | 0,18 | 0,06 | 0,06 |
3) Построим полигон относительных частот. Для построения на координатной плоскости отметим точки с координатами (xi, pi).

4) Вычислим точечные оценки:
– выборочную среднюю:

– выборочную дисперсию:
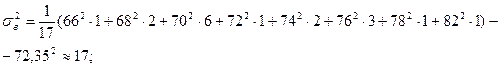
– выборочное среднее квадратическое отклонение:
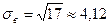 .
.
Пример 2. Пусть даны следующие результаты измерений: 82, 104, 85, 79, 87, 102, 91, 77, 88, 74, 96, 84, 63, 68, 88, 71, 85, 86, 96, 72, 77, 95, 74, 81, 85, 95, 87, 77, 82, 79, 83, 85, 93, 84, 88, 84, 86, 86, 91, 91 и выполните статистическую обработку данных по следующей схеме:
1) выполнить ранжирование признака и составить безинтервальный вариационный ряд распределения, выбрав  его значений (согласно своему варианту);
его значений (согласно своему варианту);
2) составить равноинтервальный вариационный ряд, разбив всю вариацию на 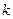 интервалов;
интервалов;
3) построить гистограмму распределения;
4) найти числовые характеристики выборочной совокупности. Для упрощения вычислений перейдите к новой варианте – 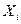 , значениями которой будут являться середы интервалов;
, значениями которой будут являться середы интервалов;
5) по результатам обработки выборочных данных выдвинуть гипотезу о нормальном распределении генеральной совокупности, например, по виду гистограммы, и выполнить ее проверку, используя правило « »;
»;
6) построить кривую нормального распределения по опытным данным, приняв в формуле Гаусса математическое ожидание 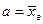 и
и  ;
;
7) найти доверительный интервал для генеральной средней 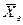 . Принять уровень значимости
. Принять уровень значимости 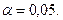
Решение:
1) В качестве выборочных данных взяли числа, находящиеся в двух первых столбцах таблицы. Выполним ранжирование выборочных данных:
 Таким образом, имеем:
Таким образом, имеем: 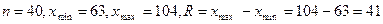 .
.
2) Для построения равноинтервального вариационного ряда:
– найдем по формуле Стерджеса число интервалов 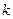 :
:  ;
;
– вычислим ширину интервала  ;
;
– вычисления границ интервалов и пр. выполним в таблице:
| Границы интервалов | [63; 69,83) | [69,83; 76,66) | [76,66; 83,49) | [83,49; 90,32) | [90,32; 97,15) | [97,15; 104) | 
|
Число попаданий в интервал, 
| |||||||
Вероятность попадания в интервал, 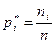
| 0,05 | 0,1 | 0,225 | 0,375 | 0,2 | 0,05 | |
Плотность вероятности, 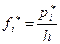
| 0,007 | 0,015 | 0,033 | 0,055 | 0,029 | 0,007 | – |
Середина интервала, 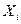
| 66,425 | 73,235 | 80,085 | 86,915 | 93,745 | 100,575 | – |
3) Построим гистограмму распределения:

4) вычислим основные числовые характеристики выборки:
– выборочную среднюю:

– выборочную дисперсию:

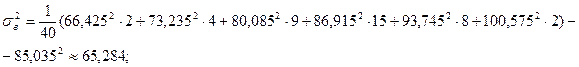
– выборочное среднее квадратическое отклонение:  .
.
5) Выдвигаем гипотезу: данная выборка сделана из нормально распределенной генеральной совокупности, о чем свидетельствует вид гистограммы распределения.
Для проверки выдвинутой гипотезы воспользуемся правилом « », согласно которому при нормальном распределении признака все его значения принадлежат интервалу (
», согласно которому при нормальном распределении признака все его значения принадлежат интервалу ( ), а значит
), а значит 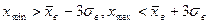 . Проверим это:
. Проверим это:
 ;
;
 .
.
Таким образом, при уровне значимости 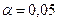 принимаем выдвинутую гипотезу: выборка принадлежит нормально распределенной генеральной совокупности.
принимаем выдвинутую гипотезу: выборка принадлежит нормально распределенной генеральной совокупности.
6) Для построения кривой нормального распределения по опытным данным примем в формуле Гаусса математическое ожидание 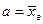 и
и  .
.
Кривая распределения представляет собой график функции плотности вероятности.
Плотность вероятности нормального распределения вычисляется по формуле Гаусса:
 ,
,
где x- значение варианты,
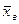 - значение выборочной средней,
- значение выборочной средней,
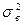 - значение выборочной дисперсии,
- значение выборочной дисперсии,
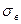 - выборочное среднее квадратическое отклонение.
- выборочное среднее квадратическое отклонение.
Для построения кривой Гаусса достаточно вычислить координаты 7 точек:
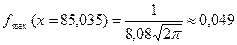 ;
;  ;
; 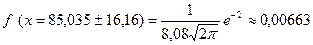 ;
;  .
.

7) найдем доверительный интервал для генеральной средней. Для этого вычислим:
–  ;
;
– 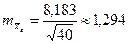 ;
;
–  , здесь
, здесь  найдено по заданным значениям
найдено по заданным значениям  и
и  (или
(или  по таблице Приложения 3;
по таблице Приложения 3;
Таким образом, получаем, что  или
или  при уровне значимости
при уровне значимости 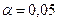 .
.
Упражнения:
1. Представить в виде статистического дискретного ряда данные о длине листьев садовой земляники (в см) и построить полигон частот: 8.2, 9.7, 6.6, 7.4, 6.4, 6.6, 8.4, 7.1, 8.0, 9.0, 6.0, 7.6, 8.1, 5.8, 7.3, 8.2, 6.4, 7.7.
2. Построить полигон частот о относительных частот по распределению выборки
| X | ||||
| m |
- Построить гистограмму относительных частот по распределению выборки
| X | 10-15 | 15-20 | 20-25 | 25-30 | 30-35 |
| m | |||||
- Построить гистограмму изменения кровяного давления у 200 практически здоровых женщин в возрасте 60-65 лет по данным статистического распределения:
| X, мм рт.ст. | m | X, мм рт.ст. | m | X, мм рт.ст. | m |
| 70-80 | 100-110 | 130-140 | |||
| 80-90 | 110-120 | 140-150 | |||
| 90-100 | 120-130 | 150-160 |
- По данным задач 2 - 4 построить эмпирическую функцию распределения.
- Построить график эмпирической функции распределения по данным выборки xi: 2,0; 2,8; 2,3; 3,4; 2,9; 2,8; 3,0; 3,2; 3,0;2,8.
- Из продукции, произведенной фармацевтической фабрикой за месяц, случайным образом отобраны 15 коробочек некоторого гомеопатического препарата, количество таблеток в которых оказалось равным соответственно 50, 51, 48, 52, 51, 50, 49, 50, 47, 50, 51, 49, 50, 52, 48. Представить эти данные в виде дискретного статистического ряда распределения, построить полигон частот, найти точечные и интервальную (с доверительной вероятностью, равной 0,95) оценки.
- При 12-кратном измерении температуры раствора серной кислоты получены следующие значения: 20,0; 20,3; 20,0; 20,2; 19,5; 20,5; 19,7; 20,0; 20,4; 20,0; 19,6; 19,8. Дать точечную и интервальную (с доверительной вероятностью, равной 0,95) оценки истинной концентрации раствора, а также вычислить относительную погрешность измерения концентрации.
- Длительность лечения больных пневмонией в стационаре (в днях): 15, 20, 18, 20, 25, 11, 12, 13, 24, 23, 24, 21, 22, 23, 23, 22, 21, 14, 14, 22, 15, 16, 20, 20, 16, 16, 20, 17, 17, 19, 19, 19, 18, 18, 18, 19, 19, 17, 17, 18. Выполните статистическую обработку данных по следующей схеме: 1) выполнить ранжирование признака и составить безинтервальный вариационный ряд распределения, выбрав
 его значений (согласно своему варианту); 2) составить равноинтервальный вариационный ряд, разбив всю вариацию на
его значений (согласно своему варианту); 2) составить равноинтервальный вариационный ряд, разбив всю вариацию на 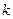 интервалов; 3) построить гистограмму распределения; 4) найти числовые характеристики выборочной совокупности. Для упрощения вычислений перейдите к новой варианте –
интервалов; 3) построить гистограмму распределения; 4) найти числовые характеристики выборочной совокупности. Для упрощения вычислений перейдите к новой варианте – 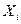 , значениями которой будут являться середы интервалов;5) по результатам обработки выборочных данных выдвинуть гипотезу о нормальном распределении генеральной совокупности, например, по виду гистограммы, и выполнить ее проверку, используя правило «
, значениями которой будут являться середы интервалов;5) по результатам обработки выборочных данных выдвинуть гипотезу о нормальном распределении генеральной совокупности, например, по виду гистограммы, и выполнить ее проверку, используя правило « »; 6) построить кривую нормального распределения по опытным данным, приняв в формуле Гаусса математическое ожидание
»; 6) построить кривую нормального распределения по опытным данным, приняв в формуле Гаусса математическое ожидание 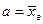 и
и  ; 7) найти доверительный интервал для генеральной средней
; 7) найти доверительный интервал для генеральной средней 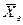 . Принять уровень значимости
. Принять уровень значимости 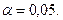
- Результаты динамометрии правой руки 40 студентов в кг: 44, 78, 47, 79, 54, 52, 56, 50, 55, 48, 51, 66, 74, 60, 42, 60, 76, 49, 45, 69, 51, 45, 46, 59, 61, 44, 62, 70, 45, 47, 44, 71, 46, 52, 43, 45, 70, 71, 53, 71. Выполните статистическую обработку данных по следующей схеме: 1) выполнить ранжирование признака и составить безинтервальный вариационный ряд распределения, выбрав
 его значений (согласно своему варианту); 2) составить равноинтервальный вариационный ряд, разбив всю вариацию на
его значений (согласно своему варианту); 2) составить равноинтервальный вариационный ряд, разбив всю вариацию на 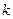 интервалов; 3) построить гистограмму распределения; 4) найти числовые характеристики выборочной совокупности. Для упрощения вычислений перейдите к новой варианте –
интервалов; 3) построить гистограмму распределения; 4) найти числовые характеристики выборочной совокупности. Для упрощения вычислений перейдите к новой варианте – 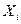 , значениями которой будут являться середы интервалов;5) по результатам обработки выборочных данных выдвинуть гипотезу о нормальном распределении генеральной совокупности, например, по виду гистограммы, и выполнить ее проверку, используя правило «
, значениями которой будут являться середы интервалов;5) по результатам обработки выборочных данных выдвинуть гипотезу о нормальном распределении генеральной совокупности, например, по виду гистограммы, и выполнить ее проверку, используя правило « »; 6) построить кривую нормального распределения по опытным данным, приняв в формуле Гаусса математическое ожидание
»; 6) построить кривую нормального распределения по опытным данным, приняв в формуле Гаусса математическое ожидание 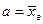 и
и  ; 7) найти доверительный интервал для генеральной средней
; 7) найти доверительный интервал для генеральной средней 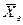 . Принять уровень значимости
. Принять уровень значимости 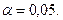
Приложение 1
 Таблица значений функции
Таблица значений функции 
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 | 0,3989 0,2420 0,0540 0,0044 |
Приложение 2
Таблица значений функции  =
= 
| x | Ф(x) | x | Ф(x) | X | Ф(x) | x | Ф(x) |
| 0,01 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,10 0,11 0,12 0,13 0,14 0,15 0,16 0,17 0,18 0,19 0,20 0,21 0,22 0,23 | 0,0000 0,0040 0,0080 0,0120 0,0160 0,0199 0,0239 0,0279 0,0319 0,0359 0,0398 0,0438 0,0478 0,0517 0,0557 0,0596 0,0636 0,0675 0,0714 0,0753 0,0793 0,0832 0,0871 0,0910 | 0,24 0,25 0,26 0,27 0,28 0,29 0,30 0,31 0,32 0,33 0,34 0,35 0,36 0,37 0,38 0,39 0,40 0,41 0,42 0,43 0,44 0,45 0,46 0,47 | 0,0948 0,0987 0,1026 0,1064 0,1103 0,1141 0,1179 0,1217 0,1255 0,1293 0,1331 0,1368 0,1406 0,1443 0,1480 0,1517 0,1554 0,1591 0,1628 0,1664 0,1700 0,1736 0,1772 0,1808 | 0,48 0,49 0,50 0,51 0,52 0,53 0,54 0,55 0,56 0,57 0,58 0,59 0,60 0,61 0,62 0,63 0,64 0,65 0,66 0,67 0,68 0,69 0,70 0,71 | 0,1844 0,1879 0,1915 0,1950 0,1985 0,2019 0,2054 0,2088 0,2123 0,2157 0,2190 0,2224 0,2257 0,2291 0,2324 0,2357 0,2389 0,2422 0,2454 0,2486 0,2517 0,2549 0,2580 0,2611 | 0,72 0,73 0,74 0,75 0,76 0,77 0,78 0,79 0,80 0,81 0,82 0,83 0,84 0,85 0,86 0,87 0,88 0,89 0,90 0,91 0,92 0,93 0,94 0,95 | 0,2642 0,2673 0,2703 0,2734 0,2764 0,2794 0,2823 0,2852 0,2881 0,2910 0,2939 0,2967 0,2995 0,3023 0,3051 0,3078 0,3106 0,3133 0,3159 0,3186 0,3212 0,3238 0,3264 0,3289 |
Приложение 2 (продолжение)
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 0,96 0,97 0,98 0,99 1,00 1,01 1,02 1,03 1,04 1,05 1,06 1,07 1,08 1,09 1,10 1,11 1,12 1,13 1,14 1,15 1,16 1,17 1,18 1,19 1,20 1,21 1,22 1,23 1,24 1,25 1,26 1,27 1,28 1,29 1,30 1,31 1,32 1,33 1,34 1,35 1,36 | 0,3315 0,3340 0,3365 0,3389 0,3413 0,3438 0,3401 0,3485 0,3508 0,3531 0,3554 0,3577 0,3599 0,3621 0,3643 0,3665 0,3686 0,3708 0,3729 0,3749 0,3770 0,3790 0,3810 0,3830 0,3849 0,3869 0,3883 0,3907 0,3925 0,3944 0,3962 0,3980 0,3997 0,4015 0,4032 0,4049 0,4066 0,4082 0,4099 0,4115 | 1,37 1,38 1,39 1,40 1,41 1,42 1,43 1,44 1,45 1,46 1,47 1,48 1,49 1,50 1,51 1,52 1,53 1,54 1,55 1,56 1,57 1,58 1,59 1,60 1,61 1,62 1,63 1,64 1,65 1,66 1,67 1,68 1,69 1,70 1,71 1,72 1,73 1,74 1,75 1,76 1,77 | 0,4147 0,4162 0,4177 0,4192 0,4207 0,4222 0,4236 0,4251 0,4265 0,4279 0,4292 0,4306 0,4319 0,4332 0,4345 0,4357 0,4370 0,4382 0,4394 0,4406 0,4418 0,4429 0,4441 0,4452 0,4463 0,4474 0,4484 0,4495 0,4505 0,4515 0,4525 0,4535 0,4545 0,4554 0,4564 0,4573 0,4582 0,4591 0,4599 0,4608 0,4616 | 1,78 1,79 1,80 1,81 1,82 1,83 1,84 1,85 1,86 1,87 1,88 1,89 1,90 1,91 1,92 1,93 1,94 1,95 1,96 1,97 1,98 1,99 2,00 2,02 2,04 2,06 2,08 2,10 2,12 2,14 2,16 2,18 2,20 2,22 2,24 2,26 2,28 2,30 2,32 2,34 | 0,4625 0,4633 0,4641 0,4649 0,4656 0,4664 0,4671 0,4678 0,4686 0,4693 0,4699 0,4706 0,4713 0,4719 0,4726 0,4732 0,4738 0,4744 0,4750 0,4756 0,4761 0,4767 0,4772 0,4783 0,4793 0,4803 0,4812 0,4821 0,4830 0,4838 0,4846 0,4854 0,4861 0,4868 0,4875 0,4881 0,4887 0,4893 0,4898 0,4904 | 2,36 2,38 2,40 2,42 2,44 2,46 2,48 2,50 2,52 2,54 2,56 2,58 2,60 2,62 2,64 2,66 2,68 2,70 2,72 2,74 2,76 2,78 2,80 2,82 2,84 2,86 2,88 2,90 2,92 2,94 2,96 2,98 3,00 3,20 3,40 3,60 3,80 4,00 4,50 5,00 | 0,4909 0,4913 0,4918 0,4922 0,4927 0,4931 0,4934 0,4938 0,4941 0,4945 0,4948 0,4951 0,4953 0,4956 0,4959 0,4961 0,4963 0,4965 0,4967 0,4969 0,4971 0,4973 0,4974 0,4976 0,4977 0,4979 0,4980 0,4981 0,4982 0,4984 0,4985 0,4985 0,49865 0,49931 0,49966 0,499841 0,499928 0,499968 0,499997 0,499997 |
Приложение 3
Таблица значений 
| n | γ | n | γ | ||||
| 0.95 | 0.99 | 0.999 | 0.95 | 0.99 | 0.999 | ||
| 2.78 2.57 2.45 2.37 2.31 2.26 2.23 2.20 2.18 2.16 2.15 2.13 2.12 2.11 2.10 | 4.60 4.03 3.71 3.50 3.36 3.25 3.17 3.11 3.06 3.01 2.98 2.95 2.92 2.90 2.88 | 8.61 6.86 5.96 5.41 5.04 4.78 4.59 4.44 4.32 4.22 4.14 4.07 4.02 3.97 3.92 | ∞ | 2.093 2.064 2.045 2.032 2.023 2.016 2.009 2.001 1.996 1.001 1.987 1.984 1.980 1.960 | 2.861 2.797 2.756 2.720 2.708 2.692 2.679 2.662 2.649 2.640 2.633 2.627 2.617 2.576 | 3.883 3.745 3.659 3.600 3.558 3.527 3.502 3.464 3.439 3.418 3.403 3.392 3.374 3.291 |
Приложение 4
Критические точки распределения Стьюдента
| Число степеней свободы V | Уровень значимости (двусторонняя критическая область) | |||||
| 0,10 | 0,05 | 0,02 | 0,01 | 0,002 | 0,001 | |
| ∞ | 6,31 2,92 2,35 2,13 2,01 1,94 1,89 1,86 1,83 1,81 1,80 1,78 1,77 1,76 1,75 1,75 1,74 1,73 1,73 1,73 1,72 1,72 1,71 1,71 1,71 1,71 1,71 1,70 1,70 1,70 1,68 1,67 1,66 1,64 | 12,7 4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26 2,23 2,20 2,18 2,16 2,14 2,13 2,12 2,11 2,10 2,09 2,09 2,08 2,07 2,07 2,06 2,06 2,06 2,05 2,05 2,05 2,04 2,02 2,00 1,98 1,96 | 31,82 6,97 4,54 3,75 3,37 3,14 3,00 2,90 2,82 2,76 2,72 2,68 2,65 2,62 2,60 2,58 2,57 2,55 2,54 2,53 2,52 2,51 2,50 2,49 2,49 2,48 2,47 2,46 2,46 2,46 2,42 2,39 2,36 2,33 | 63,7 9,92 5,84 4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,05 3,01 2,98 2,95 2,92 2,90 2,88 2,86 2,85 2,83 2,82 2,81 2,80 2,79 2,78 2,77 2,76 2,76 2,75 2,70 2,66 2,62 2,58 | 318,3 22,33 10,22 7,17 5,89 5,21 4,79 4,50 4,30 4,14 4,03 3,93 3,85 3,79 3,73 3,69 3,65 3,61 3,58 3,55 3,53 3,51 3,49 3,47 3,45 3,44 3,42 3,40 3,40 3,39 3,31 3,23 3,17 3,09 | 637,0 31,6 12,9 8,61 6,86 5,96 5,40 5,04 4,78 4,59 4,44 4,32 4,22 4,14 4,07 4,01 3,96 3,92 3,88 3,85 3,82 3,79 3,77 3,74 3,72 3,71 3,69 3,66 3,66 3,65 3,55 3,46 3,37 3,29 |
| 0,05 | 0,025 | 0,01 | 0,005 | 0,001 | 0,0005 | |
| Уровень значимости a (односторонняя критическая область) |
| Приложение 5 Критическое значение распределения Фишера-Снедекора | ||||||||||||
| f2 f1 | ||||||||||||
| При р=0,05 | ||||||||||||
| 18,51 | 19,16 | 19,25 | 19,3 | 19,33 | 19,36 | 19,37 | 19,38 | 19,39 | 19,4 | 19,41 | ||
| 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,88 | 8,84 | 8,81 | 8,78 | 8,76 | 8,74 | |
| 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,09 | 6,04 | 5,96 | 5,93 | 5,91 | ||
| 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,88 | 4,82 | 4,78 | 4,74 | 4,7 | 4,68 | |
| 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,21 | 4,15 | 4,1 | 4,06 | 4,03 | ||
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,79 | 3,73 | 3,68 | 3,63 | 3,6 | 3,57 | |
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,5 | 3,44 | 3,39 | 3,34 | 3,31 | 3,28 | |
| 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,29 | 3,23 | 3,18 | 3,13 | 3,1 | 3,07 | |
| 4,96 | 4,1 | 3,71 | 3,48 | 3,33 | 3,22 | 3,14 | 3,07 | 3,02 | 2,97 | 2,94 | 2,91 | |
| 4,84 | 3,98 | 3,59 | 3,36 | 3,2 | 3,09 | 3,01 | 2,95 | 2,9 | 2,86 | 2,82 | 2,79 | |
| 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 2,92 | 2,85 | 2,8 | 2,76 | 2,72 | 2,69 | ||
| 4,67 | 3,8 | 3,41 | 3,18 | 3,02 | 2,92 | 2,84 | 2,77 | 2,72 | 2,67 | 2,63 | 2,6 | |
| 4,6 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,77 | 2,7 | 2,65 | 2,6 | 2,56 | 2,53 | |
| 4,54 | 3,68 | 3,29 | 3,06 | 2,9 | 2,79 | 2,7 | 2,64 | 2,59 | 2,55 | 2,51 | 2,48 | |
| При р=0,025 | ||||||||||||
| 38,51 | 39,17 | 39,25 | 39,3 | 39,33 | 39,36 | 39,37 | 39,39 | 39,4 | 39,43 | 39,45 | ||
| 17,44 | 16,04 | 15,44 | 15,1 | 14,89 | 14,74 | 14,62 | 14,54 | 14,47 | 14,42 | 14,25 | 14,17 | |
| 12,22 | 10,65 | 9,98 | 9,6 | 9,36 | 9,2 | 9,07 | 8,98 | 8,9 | 8,84 | 8,66 | 8,56 | |
| 8,43 | 7,76 | 7,39 | 7,15 | 6,98 | 6,85 | 6,76 | 6,68 | 6,62 | 6,43 | 6,33 | ||
| 8,81 | 7,26 | 6,6 | 6,23 | 5,99 | 5,82 | 5,7 | 5,6 | 5,52 | 5,46 | 5,27 | 5,17 | |
| 8,07 | 6,54 | 5,89 | 5,52 | 5,29 | 5,12 | 4,9 | 4,82 | 4,76 | 4,57 | 4,47 | ||
| 7,57 | 6,06 | 5,42 | 5,05 | 4,82 | 4,65 | 4,53 | 4,43 | 4,36 | 4,3 | 4,1 | ||
| 7,21 | 5,71 | 5,08 | 4,72 | 4,48 | 4,32 | 4,2 | 4,1 | 4,03 | 3,96 | 3,77 | 3,67 | |
| 6,94 | 5,46 | 4,83 | 4,47 | 4,24 | 4,07 | 3,95 | 3,85 | 3,78 | 3,72 | 3,52 | 3,42 | |
| 6,72 | 5,26 | 4,63 | 4,28 | 4,04 | 3,88 | 3,76 | 3,66 | 3,59 | 3,53 | 3,33 | 3,23 | |
| 6,55 | 5,1 | 4,47 | 4,12 | 3,89 | 3,72 | 3,61 | 3,51 | 3,44 | 3,37 | 3,18 | 3,07 | |
| 6,41 | 4,97 | 4,35 | 3,77 | 3,6 | 3,48 | 3,39 | 3,31 | 3,25 | 3,05 | 2,95 | ||
| 6,3 | 4,86 | 4,24 | 3,89 | 3,66 | 3,5 | 3,38 | 3,89 | 3,21 | 3,15 | 2,95 | 2,84 | |
| 6,2 | 4,77 | 4,15 | 3,8 | 3,58 | 3,41 | 3,29 | 3,2 | 3,12 | 3,06 | 2,86 | 2,76 |
Приложение 6
Основные формулы дифференцирования функций
1. 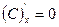
2. 
3. 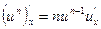

4. 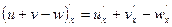
5. 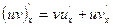
6. 

7. 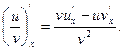
8. 
9. 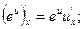
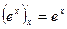
10. 
11. 
12. 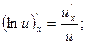

13. 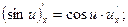

14.  ;
; 
15. 

16. 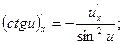
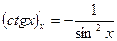
17. 

18. 
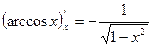
19. 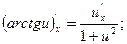

20. 
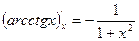
Приложение 7
Основные формулы интегрирования функций
1. 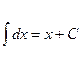 ;
;
2.  =
=  , n ¹ -1
, n ¹ -1
3.  ;
;
4.ò  ;
;
5.  ;
;
6. 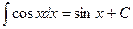 ;
;
7.  ;
;
8.  ;
;
9.  ;
;
10.  ;
;
11. 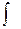
 ;
;
12. 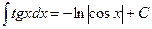 ;
;
13. 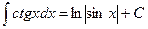 ;
;
14. 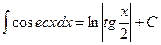 ;
;
15.  + C
+ C
16.  ;
;
17.  ;
;
18. 
 ;
;
19.  ;
;
20.  ;
;
21.  ;
;
22. 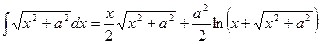 + C;
+ C;
23. 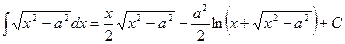 ;
;
24.  ;
;
25. 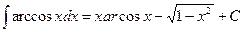 ;
;
26. 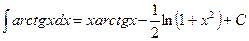 ;
;
27.  ;
;
28.  ;
;
29.  ;
;
ЛИТЕРАТУРА
1. Лобоцкая Н.Л., Морозов Ю. В., Дунаев А. А. Высшая математика.– Минск: Вышэйшая школа. 1978.
2. Основы математики и математической статистики: Учебник / И.В.Павлушков и др. – М.:ГЭОТАР-МЕД, 2003
3. Кудрявцев В.А., Демидович Б. П. Краткий курс высшей математикии. –
6-е изд. - М.:Наука, 1986.
4. Кильдишев Г. С., Френкель А. А. Анализ временных рядов и прогнозирование. - М.:Статистика,1973.
5. Гмурман В. Е. Теория вероятностей и математическая статистика. - М.: Высш. шк., 2000.
6. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. - М.:Высш. шк., 2000.
7. Гнеденко Б. В. Курс теории вероятностей. - 4-е изд. - М.: Наука. Гл. рeд. физ.–мат. лит., 1965.
8. Морозов Ю. В. Основы высшей математики и статистики: Учебник. – М.: Медицина, 1998. – 232 с.
9. Шипачев В. С. Высшая математика: Учеб. для вузов. – М.: Высшая школа, 1998. – 497с.
10. Острейковский В. А. Информатика: Учеб. пообие для тудентов ссузов. – М.: Высшая школа, 2000. – 319.
11. Информатика: Базовый курс/ С. Симонович и др. – СПб.: Питер, 2002 -640 с.
12. Гельман В. Я. Медицинская информатика: Практикум (2 – е издание). СПб.: Питер, 2002. – 480 с.
СОДЕРЖАНИЕ
| Пределы и их свойства | ||
| Дифференцирование функции одной переменной | ||
| Интегральное исчисление | ||
| 3.1. Первообразная и неопределенный интеграл | ||
| 3.2. Определенный интеграл | ||
| Дифференциальные уравнения и их применение в медицинской практике | ||
| Основы теории вероятностей | ||
| Случайные величины и их характеристики | ||
| 6.1. Дискретные случайные величины | ||
| 6.2. Непрерывные случайные величины | ||
| 6.3. Нормальное распределение непрерывной случайной величины (закон Гаусса) | ||
| Элементы математической статистики | ||
| Приложения | ||
| Литература | ||
| Содержание |
|
|
|
|
|
Дата добавления: 2015-06-26; Просмотров: 4917; Нарушение авторских прав?; Мы поможем в написании вашей работы!