Интегральная функция распределения

Непрерывная случайная величина

Случайная величина 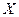называется непрерывной, если все её возможные значения полностью заполняют какой-либо конечный или бесконечный интервал числовой оси.

Для количественной характеристики распределения случайной величины 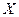вводится понятие интегральной функции pacпределения 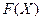случайной величины.

Интегральной функцией распределения называют функцию 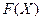, определяющую для каждого значения 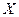вероятность того, что случайная величина 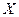примет значение меньше 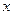, т. е. .

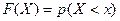Свойства функции распределения

1. Значения интегральной функции распределения принадлежат отрезку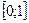

2. Функция распределения есть неубывающая функция, т. е. если .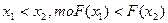

Следствие 1. Вероятность того, что случайная величина 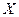попадёт в полуинтервал 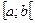, равна приращению её интегральной функции распределения на интервале : .

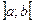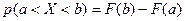Следствие 2. Вероятность того, что непрерывная случайная величина 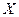примет одно определённое, заранее заданное значение равна нулю: .

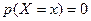3. Если возможные значения случайной величины 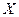принадлежат интервалу 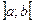, то

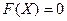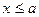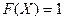при , при .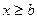

Следствие 3. Если возможные значения случайной величины 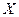расположены на всей числовой оси, то справедливы следующие предельные соотношения:

, .

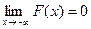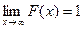Для дискретной случайной величины функция распределения определяется по формуле:

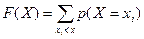, где неравенство 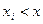под знаком суммы указывает, что суммирование распространяется на все значения 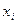, меньшие .

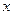Дата добавления: 2015-06-26