Закон Пуассона – закон редких событий

Пусть требуется найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность осуществления события 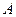очень мала, событие 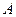наступит ровно 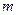раз.

В этом случае ни формула Бернулли, ни асимптотическая формула Лапласа не могут быть практически использованы для решения поставленной задачи.

При больших 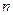и малых для вычисления искомой вероятности применяют формулу Пуассона (закон Пуассона): , где .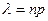

Формула Пуассона широко используется в теории массового обслуживания.

Пример 6. Вероятность заражения желудочно-кишечными заболеваниями при однократном приеме внутрь 250 мл не кипяченой речной воды составляет 0,1. Какова вероятность того, что из группы туристов, насчитывающей 6 человек, заболеет хотя бы один, если все они выпили по 250 мл не кипяченой речной воды?

Решение:

События – заражение желудочно-кишечными заболеваниями – относятся к повторным независимым испытаниям. Вероятность того, что некоторое событие 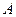произойдет ровно 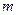раз в 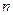испытаниях, вычисляется по формуле Бернулли:

.

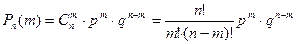По условию: 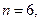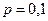, , 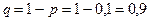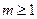(событие – «хотя бы один» – означает «один и более»), т.е. .

Известно, что сумма вероятностей событий, составляющих полную систему, равна 1, т.е. . Для данного случая имеем: или , тогда получаем, что .

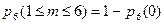Вычислим : .

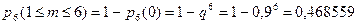Ответ: вероятность того, что из группы туристов, насчитывающей 6 человек, заболеет хотя бы один, равна .

Пример 7. Какова вероятность того, что в партии таблеток, насчитывающей 10000 штук, 1) не более 20 окажутся нестандартными, если вероятность того, что отдельная таблетка окажется нестандартной, составляет 0,0012? 2) ровно 12 штук окажутся нестандартными?

Решение:

События – нестандартная таблетка – относятся к повторным независимым испытаниям.

Число испытаний () в данном случае велико, поэтому использование формулы Бернулли для нахождения вероятности 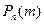приводит к вычислительным трудностям.

1) для ответа на первый вопрос используем формулу, позволяющую приближённо определять вероятность 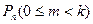, с которой происходит событие .

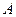По условию: , , 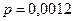, , 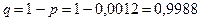. Анализ условия показывает, что 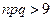, значит, для вычисления вероятности используем интегральную теорему Лапласа:

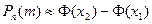, здесь – стандартный интеграл вероятностей (функция Лапласа), 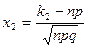, , 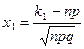причем .

Таким образом, получаем: .

По таблице значений функции 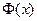находим, что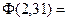 , а вероятность .

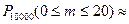
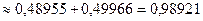2) для ответа на второй вопрос используем формулу, позволяющую приближённо определять вероятность 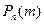, с которой происходит событие : ,

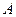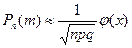где 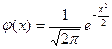, 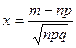(локальная теорема Лапласа).

По условию: , , , , , .

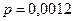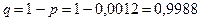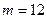Вычисляем : .

По таблице значений функции находим, что . Тогда .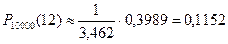

Ответ: 1) вероятность того, что в партии таблеток из 10000 штук, не более 20 окажутся нестандартными, равна ;

2) вероятность того, что в партии таблеток из 10000 штук, ровно 12 окажутся нестандартными, равна .

Пример 8. Среднее число самолетов, прибывших в аэропорт за I минуту, равно 3. Найти вероятность того, что за 2 минуты прибудут: а) не менее 3-х самолетов; б) не более 2; в) 4 самолета.

Решение:

События – прибытия самолетов в аэропорт – представляют собой простейший поток событий.

Вероятность появления 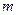событий простейшего потока за время длительностью 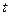определяется формулой Пуассона: , где 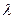– интенсивность простейшего потока, или среднее число событий, появляющихся в единицу времени.

По условию: , :

а) , т.е. 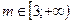. Для полной системы событий имеем: .

Или в данном случае: . Тогда интересующая нас вероятность .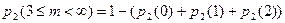

Вычисляем: , , , ,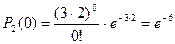

;

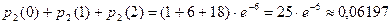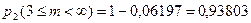б) , т.е. . Согласно теореме сложения вероятностей получаем, что . Воспользуемся вычислениями, сделанными в предыдущем пункте, и получим, что ;

в) 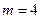. В данном случае искомая вероятность 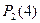вычисляется по формуле Пуассона: и будет равна .

Ответ: вероятность того, что за 2 минуты прибудут:

а) не менее 3-х самолетов, равна ;

б) не более 2, равна ;

в) 4 самолета, равна .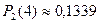

Упражнения:

Задание 1. В предлагаемом ниже перечне событий, укажите, какие из них являбтся: а) невозможными; б) достоверными; в) случайными; г) несовместными; д) независимыми; е) равновозможными; ж) зависимыми.

1. Два попадания при трех выстрелах;

2. Появление не более 18 очков при бросании трех игральных костей;

3. Наугад выбранное трехзначное число не больше 1000;

4. Из ящика с белыми шарами достают белый шар;

5. Выпадение двух и шести очков при одном бросании кубика;

6. В лототроне находятся исключительно кубики красного цвета. Событие А состоит в извлечении кубика красного цвета из лототрона;

7. В аптеке отсутствует препарат глюкоза. Событие В состоит в покупке ампул глюкозы в данной аптеке.

8. При бросании игральной два раза подряд в первый раз выпала цифра 1 (событие С₁), а во второй раз – цифра 5 (событие С₂). Событие С₁ и С₂ анализировать в совокупности, а не по отдельности.

9. При одновременном бросании двух игральных костей на одной выпала цифра 3 (событие D₁), а на другой – 6 (событие D₂). Событие D₁ и D₂ анализировать в совокупности, а не по отдельности.

10. В лототроне находятся шары с четными числами. Событие F состоит в извлечении шара с цифрой 3.

11. Наугад выбранное трехзначное число, составленное из цифр 1, 2, 3, делится на5;

12. Наугад выбранное число, составленное из цифр 1, 2, 3, 7, 8 делится на 3.

Задание 2. Решить задачи:

1. Пусть А – появление двух гербов при бросании двух момент, В- появление герба и цифры при бросании двух монет. В чем состоит событие А+В?

2. Пусть А – появление 6 очков при бросании игральной кости, В – появление 5 очков при бросании игральной кости, С – появление 4 очков при бросании игральной. В чем событие А+В+С?

3. Пусть А – появление нечетного число при бросании игральной кости, В – непоявление, С – непоявление. В чем состоят события АВС, АВ, АС, ВС?

4. Победитель соревнования может быть награжден: призом (событие ), денежной премией (событие 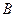), медалью (событие ). В чем состоит событие , .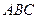

5. Подлежат контролю 250 деталей, из которых 5 бракованных. Какова вероятность того, что наудачу взятая деталь окажется: а) бракованной; в) годной.

6. Из 982 больных. Поступивших в хирургическую больницу за месяц, 275 человек имели травмы. Какова относительная частота поступления больных с этим видом заболеваний?

7. Найти вероятность выпадения нечетного числа при бросании игральной кости.

8. В урне 10 шаров: 3 белых и 7 черных. Из нее наугад извлекается один шар. Какова вероятность того, что этот шар будет белый? черный?

9. На странице книги имеется 2500 букв. Буква «а» встречается 190 раз. Какова вероятность того, что случайно выбранная буква будет буквой «а»? Какова вероятность того, что случайно выбранная не есть «а»?

10. В урне имеется 7 черных и несколько белых шаров. Какова вероятность вытащить белый шар, если вероятность вынимания черного шара равна 1/6? Сколько белых шаров в урне?

11. В каждой из двух урн имеется по 2 черных и 3 белых шара. Какова вероятность одновременного вынимания из каждой по черному шару?

12. Какова вероятность того, что в результате бросания игральной 6 раз подряд выпадут единицы?

13. Какова вероятность того, что в результате бросания игральной кости 6 раз подряд выпадут только четные числа?

14. В урне 10 шаров: 3 белых и 7 черных. Найти вероятность того, что последовательно один за другим будут вынуты шары: а) черный и белый; б) белый и черный; в)два черных; г) два белых.

15. Вероятность попадания в мишень для первого стрелка - 0,8, а для второго - 0,6. Стрелки независимо друг от друга сделали по одному выстрелу. Какова вероятность того, что в мишень попадет только один из стрелков? По крайней мере, один стрелок?

16. Охотник выстрелил три раза по удаляющейся цели. Вероятность попадания в нее в начале стрельбы равна 0,8, а после каждого выстрела уменьшается на 0,1. Найдите вероятность того, что он: а) промахнется вес 3 раза; б) попадет хотя бы один раз; в) попадет 2 раза.

17. Вероятность поражения первой мишени для данного стрелка 9/13.Если при первом выстреле зафиксировано попадание, то стрелок получает право на второй выстрел по другой мишени. Вероятность поражения обеих мишеней при двух выстрелах 0,5. Определить вероятность поражения второй мишени.

18. Четыре охотника договорились стрелять по дичи в определенной последовательности. Следующий охотник производит выстрел лишь в случае промаха предыдущего. Вероятность попадания в цель каждым из охотников одинакова и равна 0,8. Найти вероятность того, что будет произведено: а) один; б) два; в) три; г) четыре выстрела.

19. Для сообщения об аварии установлены два независимо работающих сигнализатора-автомата. Вероятность того, что при аварии сработает первый автомат, равна 0,95; второй - 0,9. Найти вероятность того, что при аварии поступит сигнал: а) хотя бы от одного сигнализатора; б) только от одного сигнализатора.

20. Экзаменационный билет содержит 3 вопроса. Вероятности того, что студент ответит на первый и второй вопросы билета, равны 0,9; на третий - 0,8. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить хотя бы на два вопроса.

21. Рабочий обслуживает три станка. Вероятность того, что в течение смены потребует его внимания первый станок, равна 0,7, второй - 0,75, третий - 0,8. Найти вероятность того, что в течение смены внимания рабочего а) потребуют какие-либо два станка; б) хотя бы один станок.

22. Два стрелка производят в цель по одному выстрелу. Вероятность попадания для первого стрелка равна 0,7, для второго - 0,8. Найти вероятность того, что попадут в цель: а) оба; б) только один; в) ни один; г) хотя бы один.

23. Рабочий обслуживает четыре станка. Вероятность того, что в течение часа первый станок не потребует внимания рабочего, равна 0,3, второй - 0,4, третий - 0,7, четвертый - 0,4. Найти вероятность того, что в течение часа а) ни один станок не потребует внимания рабочего; б) хотя бы один станок потребует внимания рабочего.

24. Радист трижды вызывает корреспондента. Вероятность того, что будет принят первый вызов, равна 0,2, второй - 0,3, третий - 0,4. Найти вероятность того, что корреспондент услышит вызов радиста.

25. Завод выпускает для магнитофонов три типа предохранителей. Доля каждого из них в общем объеме продукции составляет 30%, 50%, 20%, соответственно. При перегрузке сети предохранитель первого типа срабатывает с вероятностью 0,8, второго – 0,9 и третьего– 0,85. Определить вероятность того, что выбранный наудачу предохранитель не сработает при перегрузке сети?

26. В продукции кондитерской фабрики шоколадные конфеты составляют 40% ассортимента. В среднем 10 из 1000 шоколадных конфет оказываются с браком. Для остальной продукции этот показатель равен 5 из 200, Найти вероятность того, что; а) выбранное наугад изделие окажется без брака; б) выбранное наугад изделие без брака оказалось шоколадной конфетой.

27. Турист может пообедать в трех столовых города. Вероятность того, что он отправится к первой столовой - 1/5, ко второй - 3/5 и к третьей - 1/5. Вероятности того, что эти столовые закрыты следующие: первая - 1/6, вторая - 1/5 и третья - 1/8. Определить вероятность того, что: а) турист пообедал в одной из выбранных столовых; б) столовая, в которой пообедал студент, оказалась второй столовой?

28. На фабрике, изготавливающей некоторую продукцию, первая машина производит 30%, вторая - 45%, третья - 25% всех изделий. Брак их продукции составляет соответственно 2%, 5% и 3%. Найти вероятность того, что: а) случайно выбранное изделие оказалось дефектным; 6) случайно выбранное изделие произведено первой машиной, если оно оказалось дефектным.

29. В машбюро 5 пишущих машинок. Вероятность того, что каждая из них в течение года потребует ремонта, равна 0,2. Найти вероятность того, что в течение года не придется ремонтировать хотя бы две машинки.

30. В магазин вошли 5 покупателей. Найти вероятность того, что не менее трех из них совершат покупки, если вероятность совершить покупку для каждого вошедшего одна и та же и равна 0,3.

31. Рабочий обслуживает 5 одинаковых станков. Вероятность того, что в течение часа станок потребует регулировки, равна 1/3. Какова вероятность того, что в течение часа рабочему придется регулировать 4 станка?

32. В партии товаров имеется 400 изделий, Вероятность того, что изделие будет высшего сорта, равна 0,8. Какова вероятность того, что а) в партии товаров окажется ровно 320 изделий высшего сорта; б) число изделий высшего сорта в партии товаров будет от 310 до 330?

33. В результате проверки качества приготовленного посева зерна установлено, что 90% зёрен всхожи. Для посадки отобрано и высажено 900 зёрен. Найти вероятность того, что: а) из взятых зёрен прорастёт 820 штук; б) прорастёт от 600 до 640 посаженных зёрен.

34. Среди 1100 студентов левши составляют 1%. Чему равна вероятность того, что из общего количества студентов: а) ровно 11 левшей; б) не менее 20 левшей?

35. Среднее число самолетов, прибывших в аэропорт за 1 минуту, равно 3. Найти вероятность того, что за 2 минуты прибудут: а) не менее 3-х самолетов; б) не более 2; в) 4 самолета.

36. Среднее число кораблей, находящих в порт за 1 час, равно трем. Найти вероятность того, что за 4 часа в порт зайдут: а) 6 кораблей; б) менее 6 кораблей; в) не менее 6 кораблей.

37. Через кассу в магазине в течение 1 минуты проходит в среднем 2 человека. Найти вероятность того, что за 2 минуты пройдет: а) 4 человека; 6) не менее 2-х человек; в) не более 3-х.

38. Дискретная случайная величина Х может принимать только два значения: x₁ и x₂, причем x₁< x₂. Известны вероятность р₁ возможного значения x₁, математическое ожидание М(Х) и дисперсия D(X). Найти закон распределения этой случайной величины.

Дата добавления: 2015-06-26