Вероятность осуществления хотя бы одного события

Пусть события 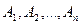независимы в совокупности и вероятности их осуществления известны: .

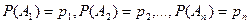Пусть в результате испытания могут осуществиться все 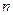событий, либо часть из них (в частности, только одно или ни одного). Требуется найти вероятность того, что наступит хотя бы одно из этих событий.

Теорема. Вероятность осуществления события 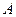, состоящего в наступле­нии хотя бы одного из событий 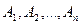, независимых в совокупности, равна разности между единицей и произведением вероятностей противо­положных событий :

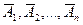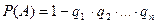, где .

Пример 2. Рабочий обслуживает 3 автоматических станка. Вероятность того, что 1-й станок будет работать без неполадок в течение часа, равна 0,9, для 2-го станка эта вероятность равна 0,8, для 3-го – 0,7. Найти вероятность того, что в течение часа все три станка будут работать без неполадок.

Решение:

Пусть А – в течение часа все три станка будут работать без неполадок,

А₁ – в течение часа 1 – й станок будет работать без неполадок,

А₂ – в течение часа 1 – й станок будет работать без неполадок,

А₃ – в течение часа 1 – й станок будет работать без неполадок.

Тогда А=А₁ А₂ А₃, и данные события независимы, следовательно, P(A) = P(A₁)P(A₂)P(A₃)=0,9×0,8×0,7=0,504.

Ответ: Вероятность того, что в течение часа все три станка будут работать бнз неполадок 0,504.

Пример 3. Из урны с пятью белыми и тремя черными шарами последовательно вынимают два шара (без возвращения в урну). Найти вероятность того, что первым появится черный, а вторым белый шар.

Решение:

Пусть А – интересующее нас событие,

А₁ – появление первым черного шара,

А₂ – появление вторым белого шара.

Тогда А=А₁ А₂ , а так как события А₁ и А₂ зависимы, то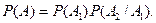

Найдем нужные вероятности по классическому определению. Так как событие А₁ появляется первым, то для него 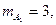следовательно,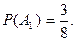

После того, как событие А₁ произошло, в урне осталось 7 шаров, из них 5 белых. Таким образом, теперь 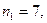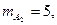следовательно, 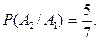Окончательно получаем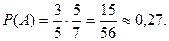

Ответ: Вероятность того, что первым появится черный, а вторым белый шар рана 0,27.

Пример 4. Центральная городская аптека закреплена за тремя больницами. Вероятность того, что в течение рабочего дня придется отпустить медикаменты первой больнице, равна 0,6, второй больнице – 0,2, третьей – 0,4. Какова вероятность того, что в течение рабочего дня придется отпустить медикаменты: 1) одной больнице? 2) по крайней мере, двум больницам?

Решение:

Пусть событие 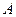состоит в том, что аптеке придется отпустить медикаменты первой больнице; вероятность этого события, по условию равна 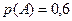, вероятность противоположного события – медикаменты отпускаться не будут – будет равна ;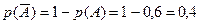

событие 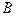состоит в том, что аптеке придется отпустить медикаменты второй больнице; вероятность этого события по условию равна 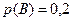, вероятность противоположного события 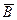– медикаменты отпускаться не будут – будет равна ;

событие состоит в том, что аптеке придется отпустить медикаменты третьей больнице; вероятность этого события по условию равна 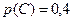, вероятность противоположного события 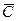– медикаменты отпускаться не будут – будет равна .

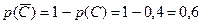1) Событие 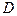– аптеке придется отпустить медикаменты одной аптеке – реализуется следующим образом: . Для нахождения вероятности этого события используем теоремы умножения и сложения вероятностей событий:

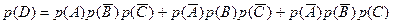
2) Событие 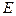– аптеке придется отпустить лекарство, по крайней мере, двум (т.е. двум или трем) больницам – включает в себя следующие события:

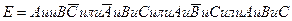. Для нахождения вероятности этого события используем теоремы умножения и сложения вероятностей событий:

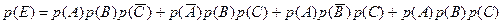, или

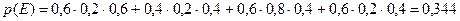
Ответ: 1) вероятность того, что центральной городской аптеке в течение рабочего дня придется отпустить медикаменты одной больнице, равна ; 2) вероятность того, что центральной городской аптеке в течение рабочего дня придется отпустить медикаменты, по крайней мере, двум больницам, равна .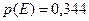

Дата добавления: 2015-06-26