Формула Бейеса

Формула полной вероятности

Пусть событие 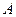может наступить при условии осуществления одного и только одного события 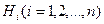из полной группы несовместных событий 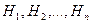. Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами.

Пусть известны вероятности 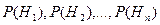этих гипотез и условные вероятности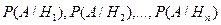 события А. Требуется найти вероятность события .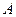

Теорема. Вероятность события 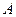, которое может наступить лишь при условии осуществления одного из несовместных событий 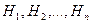, образующих полную группу событий 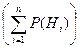, равна сумме произведений вероятностей каждой из этих гипотез на соответствующую условную вероятность события : .

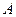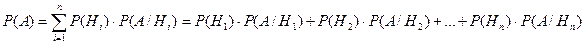Эту формулу называют формулой полной вероятности.

Пусть событие 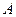может наступить при условии осуществления одного из несовместных событий (гипотез) 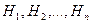, образующих полную группу событий. Пусть вероятности 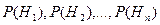известны до опыта.

Производится опыт, в результате которого осуществляется событие .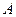

Требуется переоценить вероятности гипотез при условии, что событие 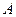уже произошло.

Переоценка вероятностей гипотез может быть осуществлена по формуле проверки гипотез (формуле Бейеса):

.

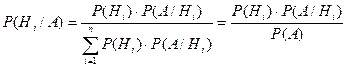Таким образом, вероятность гипотезы после опыта равна дроби, числителем которой является произведение вероятности этой гипотезы до опыта на вероятность события по этой гипотезе, а знаменателем – сумма таких же произведений для всех возможных в данном случае гипотез (или полная вероятность события ).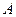

Пример 5. В цехе установлено 5 датчиков предельно допустимой концентрации пыли в воздухе, каждый из которых может включать систему сигнализации. Вероятность срабатывания первого датчика равна 0,8, второго – 0,9, третьего – 0,85, четвертого – 0,7, пятого – 0,75. 1) Найти вероятность того, что по достижении предельно допустимой концентрации пыли сигнализация сработает? 2) Сигнализация сработала. Какова вероятность того, что сигнализацию включил третий датчик?

Решение:

Пусть событие 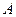состоит в том, что сигнализация сработала. Это событие может произойти только в случае появления одного из несовместных событий 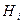– включение 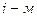датчиком сигнализации. Вероятности событий 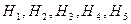по условию одинаковы и равны 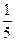. События 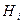образуют полную группу, т.к. .

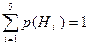Известны условные вероятности события 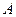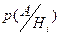– вероятности срабатывания 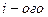датчика: , , , , .

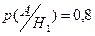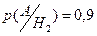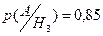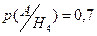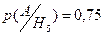1) Вероятность события 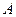вычислим по формуле полной вероятности:

, или .

2) Событие 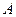произошло. Условную вероятность того, что при этом сработал третий датчик, (событие 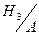) найдем по формуле Байеса: 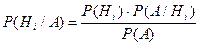, или

.

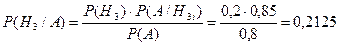Ответ: 1) вероятность того, что по достижении предельно допустимой концентрации пыли сигнализация сработает, равна ;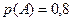

2) вероятность того, что сигнализацию при этом включил третий датчик, равна .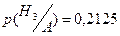

Повторные независимые испытания.

Дата добавления: 2015-06-26