
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теоретическое введение. Логические схемы и функции
|
|
|
|
Логические схемы и функции
Лабораторная работа № 11
Цель работы: Исследование логических схем. Реализация логических функций при помощи логических элементов. Синтез логических схем, выполняющих заданные логические функции.
Информация – это новые, неизвестные до данного момента сведения, которые для разных людей могут иметь разное содержание. Например, новый материал на уроках для учеников является информацией, а для учителя – повторение пройденного.
Для того чтобы систематизировать полученную информацию может быть несколько способов, но наиболее широкое применение нашли два способа – алфавитный и содержательный.
Алфавитный способ подразумевает систематизацию информации по алфавиту, не обращая внимания на содержание. Например, толковый словарь, большая советская энциклопедия, энциклопедия домашнего хозяйства и т.д.
Содержательный – разделяет информацию по внутреннему содержанию понятий. Например, справочник транзисторов, каталог книг в библиотеке, список студентов на факультете и т. д.
Единицы измерения информации: биты, байты, килобайты, мегабайты, гигабайты, но 1 байт содержит 8 бит, 1килобайт – 1024 бита (210), 1мегабайт – 1048576 бита (220), 1гигабайт – 1073741824 бита (230). Соответственно можно вывести формулу перевода информации:
х гигабайт=х*230 бит; х мегабайт=х*220 бит; х килобайт=х*210 бит
На ПК информация представляется в виде последовательностей или массивов двоичных, восьмеричных и шестнадцатеричных чисел.
С массивами двоичных чисел происходит непосредственная работа: сложение, умножение, упорядочивание, считывание и т.д.
В восьмеричном коде поступает информация с клавиатуры.
Шестнадцатеричный код предназначен для долговременного хранения информации. Этот код очень удачно ложится на байтовую систему компьютера, то есть одно шестнадцатеричное число вмещает два байта информации.
Почему же для ПК принят как основной двоичный код?
Во-первых, с технологической точки зрения легче изготовить систему, имеющую два равновесных состояния: включено – выключено или есть сигнал – нет сигнала. А в двоичной системе состояние «0» – нет сигнала, состояние «1» – есть сигнал. Если взять, например, троичную систему, то для неё необходим промежуточный сигнал. В современных цифровых системах «0» - это 0 Вольт, «1» - это 5 Вольт, значит для троичной должно быть «0» - это 0 Вольт, «1» - это 2,5 Вольт, «2» - это 5 Вольт. Разница между промежуточными состояниями 2,5 Вольта слишком мала, поэтому в случае внешних и внутренних помех система будет работать нестабильно.
Во-вторых, экономия памяти. Попробуем доказать. Возьмем счеты, как бы используя их для хранения чисел от нуля до тысячи. В десятичной системе нам потребуется три проволочки с десятью костяшками – 103. В двоичной системе необходимо десять проволочек с двумя костяшками. Сравним количество исходного материала: 3*10=30 – в десятичной системе, 10*2=20 – в двоичной системе. Экономия на 1/3.
А самое главное для двоичной системы уже существовал математический аппарат, разработанный ирландским математиком Д. Булем, а в 1948 году Шеннон доказал возможность совмещения этого аппарата с электронными устройствами.
Теперь разберем, как же кодируется информация, и, причем тут двоичный код. Разберем простейший пример на азбуке Морзе. Сигнал SOS передается «··· --- ···», передадим тот же сигнал с помощью двоичной системы, для чего сначала по таблице ASCII переведем буквы в десятичный код, затем известными нам методами в двоичный. Итак, S – 8310 (10100112), O – 7910 (10011112), то есть сигнал SOS это последовательность «1010011 1001111 1010011». Теперь понятно, что текст любой сложности это тривиальная последовательность нулей и единиц. Кодирование информации происходит с помощью кодера, обратная процедура с помощью декодера.
Труднее обстоит дело, если необходимо произвести какое-либо математическое действие, здесь не только надо перевести число в двоичную систему, но произвести с ним заданные операции. Например, надо сложить два двоичных числа: 1010011+1011001, проследим путь, который проходят числа от момента ввода до момента получения суммы (рис. 1).



рис. 1
Сначала числа поступают на общую шину данных, затем в сдвигающие регистры данных, которые, начиная с младшего разряда, подают числа в сумматор. Сумматор поразрядно выдает значение суммы, если в результате очередных разрядов получился перенос в старший разряд (1+1=10), то значение старшего разряда поступает обратно на вход. Сумматор на просто суммирует цифры, делает это с помощью специальных логических операций, которые мы разберем в следующем разделе.
Разберем подробнее алгебру Буля и соответствующее электронное обеспечение:
Она оперирует двумя понятиями: событие истинно (true) и событие ложно (false). Эти понятия ассоциируются с цифрами, используемыми в двоичной системе счисления. Событие истинно – логическая единица (1), событие ложно – логический ноль (0). Эти события являются константами.
Основное правило алгебры Буля:

Основными операциями булевой алгебры являются операции логического сложения или дизъюнкции, логического умножения или конъюнкции и отрицания или инверсии. Все операции удобно представлять в виде таблиц истинности.
Логическое сложение. Функция – ИЛИ реализует функцию логического сложения. Уровень логической 1 на его выходе появляется в том случае, если на один или на другой вход подается уровень логической единицы (табл. 1). Количество переменных над которыми выполняется операция ставится перед её обозначением, так для приведенной таблицы можно сказать, что она производит операцию 2ИЛИ. Эта операция справедлива для произвольного количества переменных. Математически она соответствует операции объединения множеств.
| х1 | х0 | х1х0(х1 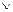 х0) х0)
|
Условное обозначение:

Логическое умножение. Функция – И реализует функцию логического умножения. Уровень логической 1 на его выходе появляется только в том случае, если на оба его входа подается уровень логической единицы (табл. 2). Эта операция справедлива тоже для произвольного количества переменных. Она соответствует математической операции пересечения множеств. Число переменных также обозначается цифрой. В приведенном примере выполняется операция 2И. Математически она соответствует операции пересечения множеств.
| х1 | х0 | х1х0(х1 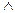 х0) х0)
|
Условное обозначение:

Логическое отрицание. Функция – НЕ или инвертор. Изменяет состояние входного сигнала на противоположное. Для её обозначения используют черту над соответствующим выражением. Операция определяется следующими постулатами:  Инвертор производит действие только над одной переменной.
Инвертор производит действие только над одной переменной.
Условное обозначение:

Стрелка Пирса или функция ИЛИ-НЕ: это операция отрицания логической суммы
| х1 | х0 |  х1↓х0(х1 х1↓х0(х1 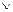 х0) х0)
|
Условное обозначение

Штрих Шеффера или функция И-НЕ: это операция отрицания логического произведения
| х1 | х0 | х1х0(х1 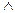 х0) х0)
|
Условное обозначение

Теоремы алгебры Буля:
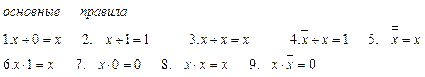
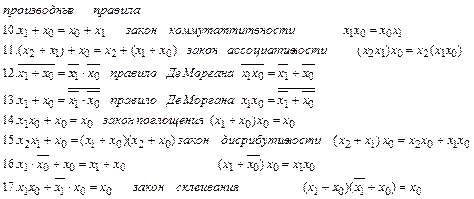
Зависимость выходных переменных, выраженная через совокупность входных переменных с помощью операций алгебры логики, называется функцией алгебры логики ФАЛ.
Для описания ФАЛ используют различные способы. Обычно применяют их последовательно для получения ФАЛ.
1. Описание функции в словесной форме
2. Описание функции в виде таблиц истинности
3. Описание функции в виде алгебраического выражения
Словесное описание ФАЛ
Логическая функция трех переменных равна единице, если равен единице х1. Это применяется для первоначального, исходного описания работы логического устройства.
Описание ФАЛ в виде таблицы истинности. Таблица, содержащая все возможные комбинации входных переменных и соответствующие им значения выходных переменных называется таблицей истинности или комбинационной таблицей. Таблица содержит (п+1) столбец, где п – количество входных переменных и (2п+1) строк. Для заданного словесного описания таблица будет выглядеть следующим образом (табл. 3):
(табл. 3)
| х2 | х1 | х0 | у |
Описание функции в виде алгебраического выражения. Для этого используются две стандартные формы её представления.
1. Дизъюнктивная нормальная форма ДНФ
2. Конъюнктивная нормальная форма КНФ
дизъюнктивная нормальная форма
1). Находим конституенты единицы, т. е. для значений выходной переменной равной единице записываем логические произведения соответствующих входных переменных, причем значения входных переменных равные нулю записываются с инверсией.
2). Записываем логические суммы полученных конституент единицы.
В итоге получаем: 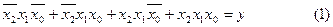
конъюнктивная нормальная форма
1). Находим конституенты нуля, т. е. для значений выходной переменной равной нулю записываем логические суммы соответствующих входных переменных, причем значения входных переменных равные единице записываются с инверсией.
2). Записываем логические произведения полученных конституент нуля
В итоге получаем: 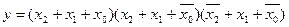
По полученным ФАЛ можно построить логическую схему.
получится следующая схема (рис.2).

рис 2
Схема довольно сложная, в ней используется много элементов, поэтому все ФАЛ необходимо минимизировать для оптимальной её реализации. Минимизация производится обычно двумя способами:
1). Вынесение за скобку для применения правила 4 алгебры Буля
2). Добавление однотипных элементов для вынесения за скобку
3). Применение правила Де Моргана (12, 13).
4). Остальные правила применяются по мере необходимости.
после упрощения получаем: у=х1. Схема естественно сильно упрощается.
Задание
Исследовать логические элементы со следующим соответствием сигналов:
0В – сигнал 0 – низкий потенциал
1В – сигнал 1 – высокий потенциал
По соответствующим схемам заполнить таблицы истинности
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 412; Нарушение авторских прав?; Мы поможем в написании вашей работы!