Теоретическое введение. Исследование работы комбинационных логических схем

Исследование работы комбинационных логических схем

Комбинационной схемой называется логическая схема, реализующая однозначное соответствие между значениями входных и выходных сигна­лов. В комбинационных схемах используются логические элементы, выпус­каемые в виде интегральных схем. В этот класс входят интегральные схемы дешифраторов, шифраторов, мультиплексоров, демультиплексоров и сумматоров.

Шифратором или кодером называется комбинационное логическое устройство для преобразования чисел из десятичной системы счисления в двоичную. Основное применения шифратора в цифровых системах – это введение первичной информации с клавиатуры.

Дешифратором или декодером называется комбинационное логиче­ское устройство для преобразования чисел из двоичной системы счисления в десятичную. Дешифратор имеет 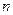информационных входов, которым соот­ветствует 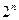выходов. Каждой комбинации логических уровней на входах будет соответствовать активный уровень на одном из 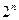выходов. Обычно число входов равно 2, 3 или 4. Если числу входов 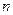соответствует 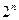выхо­дов, то дешифратор называют полным, если меньше, то неполным. На рис. 1 де-шифратор имеет три входа, активным уровнем является уровень логиче­ского нуля. На входы С, В, А можно подать такие комбинации уровней: 000,001,010,011,... 111, всего 8 комбинации.

Рис. 12.1

Схема имеет восемь выводов (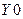, , , , 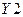, , 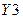, 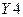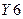), на одном из них формируется низкий потенциал или логический нуль, на остальных – высокий или логическая единица. Номер этого выхода определяется по известной формуле перехода от системы счисления с меньшим основанием к системе счисления с большим основанием, где произвольное число 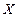в по­зиционной системе счисления с основанием 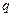можно представить в виде полинома:

так как мы имеем три входа – А, В, С, то есть 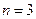, то

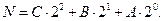
Например, если на входы подана логическая комбинация 011, что со­ответствует в десятичной системе счисления числу 3, то сигнал логического нуля установится на выходе номер три (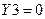), что можно подсчитать по формуле: 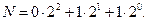, а все остальные выходы будут иметь сигнал логической единицы. Этот принцип формирования выходного сигнала мож­но описать следующим образом:

Уровень сигнала на выходе 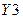можно описать выражением ФАЛ:

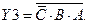
ФАЛ для остальных выходов:

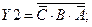
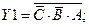
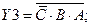
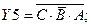
Кроме информационных входов А, В, С, дешифраторы имеют допол­нительные управляющие входы G. Сигналы на этих входах разрешают рабо­ту дешифратора или переводят его в пассивное состояние, при котором, не­зависимо от сигналов на информационных входах, на выходе все сигналы имеют уровень логической единицы.

Разрешающий вход дешифратора может быть прямым и инверсным. У дешифраторов с прямым входом разрешения активным является уровень ло­гической единицы, дешифраторов с инверсным входом разрешения актив­ным является уровень логического нуля. На рис. 1 представлен дешифратор с одним инверсным управляющим входом. Принцип формирования выход­ного сигнала в этом дешифраторе с учетом сигнала управления описывается следующим образом:

У дешифраторов с несколькими входами управления функция разре­шения представляет собой логическое произведение всех разрешающих сиг­налов управления. Например, для дешифраторов 74138 с одним прямым входом управления 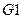и двумя инверсными и 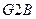(рис. 2) функция разрешения имеет вид: .

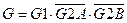Обычно входы управления используются для каскадирования (увели­чения разрядности) дешифраторов или при параллельной работе нескольких схем на общие выходные линии.

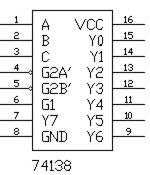
Рис. 12.2

Дешифратор может быть использован и как демультиплексор – логи­ческий коммутатор, подключающий входной сигнал к одному из выходов. Демультиплексор имеет один информационный вход, адресных и 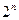выхо­дов. В случае использования дешифратора как демультиплексора, роль ин­формационного входа играет один из входов разрешения, а состояние выхо­дов А, В, С задает номер выхода, на который передается сигнал со входа разрешения.

Мультиплексором называется комбинационное логическое устройст­во, предназначенное для управляемой передачи данных от нескольких ис­точников информации в один выходной канал. Типовое применение мульти­плексора это передача информации от нескольких, разнесенных в про­странстве источников (датчиков) информации на вход одного приемника. Например, изменение температуры блоков ядерного реактора. Температуру измеряют через фиксированные промежутки времени, но промежуток вре­мени между двумя измерениями должен быть много меньше, чем постоян­ной времени, характеризующей изменение температуры. Мультиплексор подключает различные датчики температуры к одному приемнику по задан­ной команде. Мультиплексор также можно назвать управляемым переклю­чателем. Согласно определению, мультиплексор должен иметь один выход и две группы входов: информационные , , , , 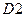, , 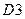, 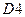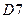и ад­ресные А, В, С (рис. 3). Мультиплексор подключает к выходу один из информационных входов данных. Номер подключаемого входа равен числу (адресу), определяемому комбинацией логических уровней на входах управ­ления. Если число адресных входов равняется , то информационных входов будет .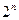

Кроме информационных и управляющих (адресных) входов, схемы мультиплексоров имеют вход разрешения G, при подаче на него сигнала ло­гической единицы мультиплексор переходит в активное состояние, при по­даче логического нуля мультиплексор перейдет в пассивное состояние, для которого сигнал на выходе не меняется, независимо от значений информа­ционных и управляющих сигналов. Мультиплексор, представленный на рис. 1 имеет два выхода прямой Y и инверсный W(W= Y).

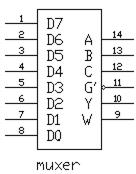
Рис. 12.3

Функция алгебры логики (ФАЛ) мультиплексора, представленного на рис. 1, связывающая сигнал на выходе (), с разрешающим входом (G), вход­ными информационными (, , , , 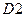, , 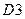, 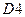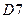) и управляющими (А, В, С) сигналами

(1)

Из уравнения видно, что на мультиплексоре можно реализовать логи­ческие функции, для этого необходимо определить, какие сигналы и логиче­ские константы следует подавать на входы мультиплексора.

Так как логическая функция переменных определена для 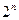комби­наций значений переменных, то это позволяет реализовать функцию – пе­ременных на мультиплексоре, имеющем – управляющих (адресных) и 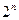– информационных входов. В этом случае каждой комбинации значений аргу­ментов соответствует единственный информационный вход мультиплексора, на который подается значение функции. Например, требуется реализовать функцию

(2)

Эта функция определена только для 8 комбинаций значений перемен­ных, поэтому для её реализации можно использовать мультиплексор 8x1 с тремя адресными входами. Составим таблицу истинности этой функции (табл. 1)

Таблица 1

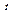
Из таблицы видно, что для реализации функции на мультиплексоре необходимо подать на информационный вход мультиплексора с номером N сигнал, значение которого равно соответствующему значению функции F 1, то есть на входы с номерами 1, 2, 4, 5 следует подавать уровень логического нуля, а на остальные - уровень логической единицы. Таким образом, при подаче комбинаций логических уровней на управляющие входы мультип­лексора, к его выходу подключится вход, значение сигнала на котором равно соответствующему значению функции. Схема, реализующая эту функцию приведена на рис. 4.

Рис.12.4

При реализации логических функций на информационные входы мож­но подавать не только константы, но и изменяющиеся входные сигналы. Так, например, рассмотрим другой способ реализации функции F 1. Для этого не­обходимо минимизировать выражение функции:

(3)

Таблица истинности этой функции представлена в табл. 2. Заданную такой таблицей функцию реализуют, как и в предыдущем случае, подав на вход с номером N сигнал, значение которого соответствует значению функции F 1.

Таблица 2

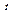
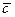
В данном случае сигналы и 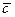, соответствующие переменной , по­даются на информационные входы. При этом сокращается число адресных входов. Схема реализации такого способа представлена на рис. 5.

Так как используется только два адресных входа, то вход С можно за­землить, при этом состояние информационных входов D 4... D 7 безразлично. Уровень сигнала на выходе схемы определяется комбинацией уровней сиг­налов в точках А, В, С соответствующих переменных а, 6, с. Схема на рис. 3 представляет собой мультиплексор 4x1 с двумя адресными и четырьмя ин­формационными входами.

Рис. 12.5

Функция, представленная в виде произведения одночлена на много­член, также может быть реализована на мультиплексоре. Из уравнения мультиплексора следует, что сигнал, соответствующий одночлену надо по­давать на вход разрешения. Например, функция описывается следующим выражением:

(4)

При реализации данной функции сигнал, соответствующий перемен­ной следует подавать на его разрешающий вход. Выражение в скобках можно рассматривать как некоторую функцию пяти переменных из которых наиболее часто используются переменные . Поэтому сигналы, соответствующие этим переменным следует подавать на адресные входы мультиплексора.

Для определения сигналов, которые необходимо подавать на инфор­мационные входы, чтобы реализовать функцию необходимо составить таблицу истинности функции в зависимости от значений переменных (табл. 3). Из таблицы видно, что на информационные входы с номерами 0, 2, 4, 6 надо подать сигнал логического нуля. Сигнал, соответствующий пере­менной , нужно подать на входы с номерами 1 и 5, переменной 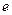– на вход с номером 3. Схема, реализующая эту функцию представлена на рис. 6.

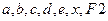
Рис. 10.6

Таблица 3

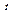
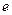
Дата добавления: 2015-06-04