Силовые линии. Поток вектора напряженности. Теорема Остроградского-Гаусса

Силовой линией электростатического поля называется линия, касательная к которой в каждой точке совпадает с направлением вектора 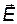(рис. 1.5).

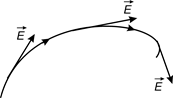Рис. 1.5

Свойства силовых линий:

а) силовые линии электростатического поля не пересекаются;

б) силовые линии электростатического поля разомкнуты - они начинаются на положительных зарядах и заканчиваются на отрицательных (или уходят в бесконечность).

Введем понятие потока вектора напряженности поля 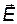. По определению элементарный поток вектора напряженности через площадку dS

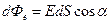
(1.11)

где a - угол между вектором 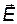и нормалью к площадке (рис. 1.6).

Выражение (1.11) можно представить как скалярное произведение

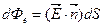
(1.12)

где 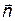– единичный вектор, совпадающий с нормалью.

Суммарный поток вектора напряженности через какую-либо поверхность можно найти интегрированием (11.12) для всей поверхности 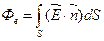для замкнутой поверхности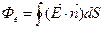

Важнейшую роль в электростатике играет теорема Остроградского ‑ Гаусса, которая формулируется следующим образом: поток вектора напряженности через любую замкнутую поверхность пропорционален алгебраической сумме зарядов, находящихся внутри этой поверхности:

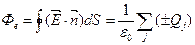, (1.13)

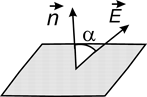Рис. 1.6

Доказательство. Рассмотрим простейший случай, когда замкнутая поверхность представляет собой сферу, в центре которой находится точечный заряд +Q (рис. 1.7). Выделим на сфере элементарную площадку dS. Нормаль к этой площадке и вектор 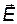совпадают по направлению, поэтому .

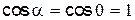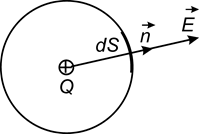Рис. 1.7

Преобразуем подынтегральное выражение в (1.13) следующим образом:

,

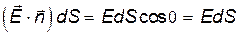Принимая во внимание, что всюду на поверхности сферы E=const, и учитывая выражение (11.6), получим:

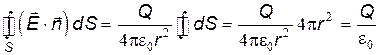
Теорема доказана для частного случая, когда внутри сферической поверхности имеется один заряд. Доказательство легко обобщается на случай произвольного числа зарядов и произвольной замкнутой поверхности.

В суммарном потоке, который создают заряды, расположенные за пределами замкнутой поверхности, можно выделить положительную и отрицательную части, которые взаимно компенсируются. Поэтому внешние по отношению к данной замкнутой поверхности заряды в теореме Остроградского – Гаусса не учитываются.

Теорема Остроградского-Гаусса связывает заряды с создаваемыми ими электрическими полями и отражает тот факт, что источником электростатического поля служат неподвижные электрические заряды.

Эта теорема тесно связана с законом Кулона: если справедлив закон Кулона, то справедлива и теорема Остроградского-Гаусса, и наоборот. Если бы в законе Кулона показатель степени хотя бы незначительно отличался от двух, т.е. F~1/r^2+α, где α –сколь угодно малое число, то теорема Остроградского-Гаусса нарушалась бы. Справедливость теоремы Остроградского-Гаусса проверена на опыте с гораздо большей точностью, чем закон Кулона.

Дата добавления: 2015-06-04