Напряженность поля бесконечной равномерно заряженной нити с линейной плотностью заряда

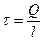[ Кл/м ]

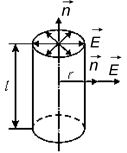Рис. 1.10

Используя теорему Остроградского-Гаусса, можно показать, что в этом случае

.

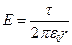(1.16)

При выводе формулы (1.16) следует выбрать замкнутую поверхность в виде цилиндра (рис. 1.10) и учесть, что вектор 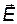перпендикулярен к нити и поэтому поток вектора 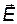через основания цилиндра равен нулю.

11.6. Работа по перемещению заряда в электростатическом поле. Теорема о циркуляции вектора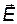

Найдем элементарную работу по перемещению заряда q в поле, создаваемом зарядом Q:

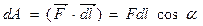где a – угол между силой 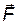и направлением перемещения .

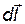Из рис. 1.11 видно, что 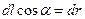.поэтому

Суммарную работу но перемещению заряда q из точки А в точку B получим интегрированием выражения (11.17). Используя закон Кулона, получаем . Окончательно

, (1.18)

Если заряд перемещается из точки A в точку B по другому пути, то, проделав такие же выкладки, снова придем к формуле (11.18). Следовательно, работа в электростатическом поле не зависит от формы пути, а зависит лишь от выбора начальной и конечной точки. Кроме того, как видно из (11.18), работа по перемещению заряда в электростатическом поде по замкнутому контуру равна нулю, т.е. , (1.19)

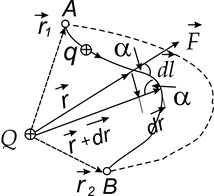Рис. 1.11

Эти признаки означают, что электростатическое поле является потенциальным. В соответствии с результатом, полученным в § 3.3,работу потенциальных (консервативных) сил можно выразить через разность потенциальных энергий:

Из сопоставления (11.18) и (11.20) заключаем, что потенциальная энергия взаимодействия двух точечных зарядов

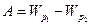.	(1.20)
.	(1.21)

Введем теперь энергетическую характеристику электростатического поля – потенциал. Потенциалом называется скалярная величина, численно равная потенциальной энергии единичного положительного заряда, помещенного в данную точку поля:

.

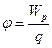(1.22)

Единицей потенциала электростатического поляявляется вольт. Один вольт – это потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией в 1 Дж: 1 В = 1 Дж/Кл.

Потенциал поля точечного заряда найдем, подставив (1.21) в (1.22):

.

(1.23)

И, наконец, с помощью (1.22) выражение (1.20) для работы по перемещению заряда в электростатическом поле из одной точки в другую можно представить как произведение заряда на разность потенциалов:

.

(1.24)

Преобразуем теперь выражение (11.19) следующим образом:

.

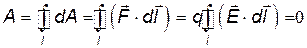(1.25)

где учтено, что сила, действующая на заряд в электростатическом поле,

.

(1.26)

а кружок означает, что интегрирование проводится по замкнутому контуру.

Из (1.25) следует

.

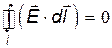(1.27)

Интеграл, фигурирующий в (1.27), называется циркуляцией напряженности электростатического поля. Из (1.27) видно, что циркуляция вектора 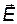равна нулю. Этот результат получен из того факта, что работа в электростатическом поле не зависит от формы пути. Поэтому равенство нулю циркуляции вектора 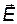есть также признак того, что электростатическое поле является потенциальным.

Дата добавления: 2015-06-04