Энергия заряженного конденсатора. Плотность энергии электростатического поля

Энергия заряженного проводника

Заряд, расположенный на поверхности проводника, можно рассматривать как систему точечных зарядов, поэтому для вычисления энергии заряженного проводника можно воспользоваться формулой (14.4). Потенциал любой точки поверхности проводника одинаков (j_i=j), поскольку его поверхность эквипотенциальна. Следовательно, в формуле (14.4) потенциал можно вынести за знак суммы:

или , (14.5) где 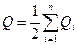– заряд проводника.

С учётом (13.3) выражение для энергии заряженного проводника можно представить в виде

(14.6)

или

(14.7)

Для вычисления энергии заряженного конденсатора воспользуемся формулами (14.5) – (14.7), заменив j на разность потенциалов между обкладками конденсатора U=j₁-j₂. Тогда

,	(14.8)
	(14.9)
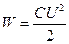
	(14.10)

Дальнейшее рассмотрение проведём, основываясь на формуле (14.9). Представим заряд конденсатора как Q=sS, где s – поверхностная плотность заряда, а S – площадь обкладки конденсатора. Воспользовавшись далее выражением для ёмкости плоского конденсатора (13.7), представим (14.9) в виде

,

(14.11)

где V=Sd – объём конденсатора.

С помощью (11.15) выразим поверхностную плотность заряда s через напряжённость поля E и подставим полученное выражение в (14.11). В результате получим

,

(14.12)

В формуле (14.9) энергия заряженного конденсатора выражена через заряд на его обкладках и ёмкость. В формуле (14.12) энергия конденсатора выражена через напряжённость электростатического поля, сосредоточенного между его обкладками. В связи с этим возникает принципиальный вопрос о том, что служит носителем энергии конденсатора: заряды или электростатическое поле. Этот вопрос – центральный в длительной дискуссии между сторонниками дальнодействия и близкодействия.

Сторонники дальнодействия отдавали предпочтение формуле (14.9), рассматривая её как потенциальную энергию взаимодействия двух тел. Приверженцы этой теории отвергали возможность осуществления взаимодействия посредством поля.

Сторонники теории близкодействия (полевой теории) считали, что энергия конденсатора есть энергия электростатического поля (формула (14.2)). Эта энергия "размазана" по всему объёму конденсатора и, следовательно, можно говорить об объёмной плотности энергии:

[Дж/м³] или , С учётом (12.11) формулу (14.13) можно представить в виде

(14.14)

В рамках электростатики решить вопрос, что является носителем энергии – заряды или поле, невозможно, поскольку неподвижные заряды и создаваемое ими электростатическое поле неотделимы друг от друга. При изучении переменных электрических и магнитных полей оказалось, что электромагнитное поле может отрываться от зарядов, существуя независимо от них. Это и есть решающий аргумент в пользу теории близкодействия (полевой теории).

Лекція 23.

Дата добавления: 2015-06-04