Правила Кирхгофа. Обоснование законов Ома и Джоуля-Ленца по классической электронной теории

Обоснование законов Ома и Джоуля-Ленца по классической электронной теории

В классической электронной теории металлов принимается следующая модель.

1. Носителями тока в металлах являются свободные электроны.

2. Свободные электроны образуют электронный газ, который по своим свойствам аналогичен идеальному газу. Имеется лишь одно различие: электроны при своем движении сталкиваются не между собой, а с ионами кристаллической решетки.

3. Под действием электрического поля электроны наряду с хаотическим движением со скоростью 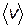начинают двигаться направлено со скоростью 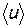. При этом скорость направленного движения значительно меньше скорости хаотического движения

.

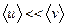(15.21)

Найдем скорость направленного движения электронов. Предположим, что в момент времени t=0 скорость направленного движения электронов u₀=0. Под действием силы F=eE электрон в соответствии со вторым законом Ньютона начинает двигаться ускоренно:

.

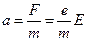Скорость направленного движения электрона

.

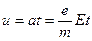(15.22)

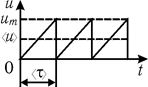Рис. 15.4

Из формулы (15.22) следует, что скорость электрона u с течением времени должна возрастать неограниченно. Однако через некоторый промежуток времени t электрон испытывает столкновение с ионом кристаллической решетки и останавливается. Схематически зависимость скорости направленного движения от времени изображена на рис. 15.4.

Среднее время между двумя последовательными столкновениями электрона

,

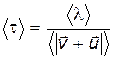(15.23)

где 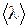– средняя длина свободного пробега электрона; 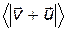– среднее значение его скорости, которая является векторной суммой скоростей хаотического и направленного движений.

В силу неравенства (15.21) скоростью направленного движения можно пренебречь, поэтому

.

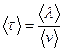(15.24)

Заменив в формуле (15.22) время t на t, найдем максимальную скорость направленного движения электрона

.

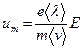(15.25)

Средняя скорость направленного движения электрона

.

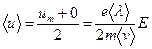(15.26)

Подставим (15.26) в выражение для плотности тока (15.3):

.

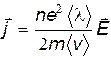(15.27)

Из сопоставления (15.27) и (15.15) видно, что удельная проводимость металла

.

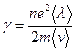(15.28)

Тем самым удалось не только теоретически обосновать закон Ома, но и выразить удельную проводимость и, следовательно, удельное сопротивление

.

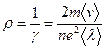(15.29)

через характеристики электронного газа.

Исходя из представлений классической электронной теории металлов, получим теперь закон Джоуля–Ленца.

К концу свободного пробега электрон обладает кинетической энергией направленного движения 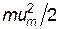. Эту энергию электрон полностью передает иону кристаллической решетки при столкновении с ним. Множество таких столкновений приводит к выделению джоулевой теплоты. Если концентрация электронов n, и каждый из них сталкивается 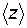раз за 1 с, то в единичном объеме проводника выделиться мощность

.

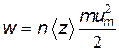Подставляя сюда значение максимальной скорости направленного движения электрона из (15.25) и учитывая, что среднее число столкновений за 1 с

,

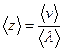получаем закон Джоуля–Ленца

.

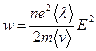(15.30)

Из сопоставления (15.30) и (15.20) находим такое же выражение для удельной теплопроводности, как и в законе Ома (см. (15.28)).

Несмотря на очевидные успехи классической электронной теории металлов, она, тем не менее, столкнулась с рядом трудностей. В частности классическая теория неправильно предсказывает зависимость сопротивления металла от температуры. Анализ выражения (15.29) показывает, что от температуры зависит лишь скорость хаотического движения. При этом (см. формулу (8.18)) 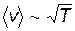, следовательно, удельное сопротивление 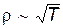. Между тем опыт показывает, что r линейно зависит от температуры ,

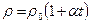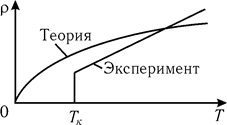Рис. 15.5

где r₀ – удельное сопротивление при температуре t=0 ⁰C; a – температурный коэффициент сопротивления. Более того, в области низких температур (T < T_к) сопротивление многих металлов скачком обращается в нуль – наступает явление сверхпроводимости (рис. 15.5).

Трудности классической теории были устранены квантовой теорией электропроводности (§ 31.3).

Для расчета сложных цепей постоянного тока применяют правила Кирхгофа.

Первое правило Кирхгофа. Алгебраическая сумма токов, сходящихся в узле, равна нулю, т.е.

.

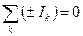(15.31)

Узлом называется точка цепи, где пересекаются три и более проводников. Ток берется со знаком "+", если он входит в узел; выходящий из узла ток берется со знаком "-".

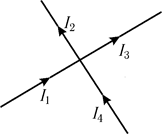Рис. 15.6

Для узла показанного, на рис. 15.6, первое правило Кирхгофа записывается в виде 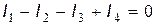, или ,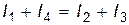

т.е. сумма токов, входящих в узел, равна сумме токов, выходящих из него.

Первое правило Кирхгофа – следствие закона сохранения электрического заряда: заряды, попав в узел, никуда не исчезают и не накапливаются.

Второе правило Кирхгофа. Алгебраическая сумма падений напряжения в замкнутом контуре, выделенном из сложной цепи, равна алгебраической сумме ЭДС, включенных в этот контур:

.

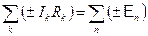(15.32)

Падение напряжения берется со знаком "+", если ток направлен в сторону обхода контура, и "-" в противном случае. ЭДС берется со знаком "+", если она действует в направлении обхода, и "-" – в противном случае. Направление обхода выбирается произвольно. Для определенности выберем направление обхода по часовой стрелке.

Запишем для примера второе правило Кирхгофа для контуров ABCFA и ABCDEFA (рис. 15.7):

контур ABCFA: I₁R₁ + I₂R₂= E ₁ – E₂;

контур ABCDEFA: I₁R₁ - I₃R₃= E ₁ – E₃.

В общем случае, когда в цепи имеется n узлов и m контуров, нужно составить n-1 уравнение по первому правилу Кирхгофа и m-1 уравнение по второму правилу.

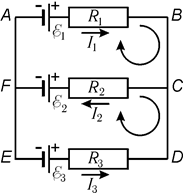Рис. 15.7

Лекція 25.

Дата добавления: 2015-06-04