Магнитное поле кругового тока

Магнитное поля прямолинейного проводника с током

Найдем вектор магнитной индукции в точке A, отстоящей от прямолинейного проводника с током на расстояние R. С этой целью воспользуемся законом Био–Савара–Лапласа (17.16). Для вычисления интеграла (17.16) выразим переменные r и dl через q.

Согласно рис. 17.4 имеем

; .

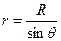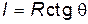(17.18)

Рис. 17.4

Продифференцируем последнее равенство

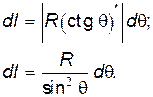
(17.19)

С помощью (17.18) и (17.19) подынтегральное выражение в (17.16) можно преобразовать к виду

.

Подставим полученное выражение в формулу (17.16) и проинтегрируем в пределах от q₁ до q₂ (рис. 17.4).

(17.20)

Формула (17.20) применима для проводника единичной длины. Для бесконечно длинного проводника следует положить q₁ = 0, q₂ = p. Тогда из (17.20) следует

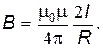
(17.21)

Пусть по проводнику в виде тонкого кольца радиуса a протекает ток I. Найдем вектор магнитной индукции в точке A, расположенной на оси кольца и отстоящей от его центра на расстоянии R (рис. 17.5).

Выделим на кольце элемент тока Idl. В точке A он создает вектор магнитной индукции 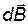. Разложим 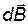на две составляющие:

.

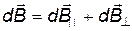Перпендикулярная составляющая не дает никакого вклада в общую индукцию в точке A, поскольку на кольце всегда найдется симметрично расположенный элемент тока Idl, который дает

противоположно направленную составляющую .

Рис. 17.5

Из рис. 17.5 видно, что

.

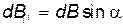Так как 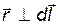, то sin q = 1, следовательно,

;

.

Интегрируя по всему контуру, получаем:

,

,

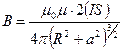где S – площадь, охваченная круговым током.

Произведение силы тока I на площадь, ограниченную круговым током, называется магнитным моментом кругового тока (витка):

,

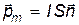(17.22)

Рис. 17.6

где – единичный вектор, перпендикулярный к плоскости витка с током. Направление находится по правилу правого винта (рис. 17.6).

Таким образом, модуль вектора магнитной индукции на оси кругового тока

.

(17.23)

При R>>a из (17.23) следует

.

(17.24)

Сопоставляя (17.24) и (11.9), приходим к выводу, что круговой виток с током создает магнитное поле, которое, как и электрическое поле диполя, на больших расстояниях убывает как 1/R³.

В центре кругового витка (R=0) из формулы (17.23) получаем

.

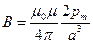Поскольку p_m=IS=Ipa², то

.

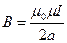(17.25)

Лекція 27.

17.6. Циркуляция вектора

В электростатике было показано, что циркуляция вектора напряженности электростатического поля равна нулю (см. § 11.6). Этот результат свидетельствует о потенциальном характере электростатического поля.

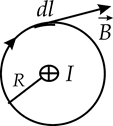Рис. 17.7

Выясним теперь, сему равна циркуляция вектора магнитной индукции . Рассмотрим простейший случай, когда магнитное поле создаётся бесконечным прямолинейным проводником, а контур интегрирования совпадает с линией индукции. Тогда выражение для циркуляции вектора сучётом(17.21) будет иметь вид

.

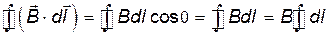(17.26)

Подставляя в (17.26) значение из (17.21) и учитывая, что , получаем

.

(17.27)

Выражение (17.27) можно обобщить на случай, когда контур имеет произвольную форму и охватывает несколько проводников с током:

.

(17.28)

Знак "+" в формуле (17.28) выбираем в том случае, если направление тока и направление обхода удовлетворяют правилу левого винта, и "–" – в противном случае.

Как видно из (17.28), циркуляция вектора магнитной индукции отлична от нуля. Это означает, что магнитное поле имеет непотенциальный характер – для него нельзя ввести понятие потенциала. Магнитное поле является вихревым.

Если учесть, что B= m₀ mH, то из (17.28) можно получить выражение для циркуляции вектора напряженности магнитного поля:

.

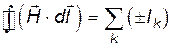(17.29)

Последнюю формулу называют иногда законом полного тока.

Формулы (17.28) и (17.29) применяют для расчета магнитных полей. В некоторых случаях такой расчет значительно проще, чем основанный на законе Био–Савара–Лапласа.

Дата добавления: 2015-06-04